Cohete propulsado por un gas a presión

Sea un recipiente cilíndrico, situado en el vacío, con un émbolo que se puede desplazar sin rozamiento en su interior. Se fija el émbolo y el recinto se llena de gas a alta presión. Se libera el émbolo, el gas se expansiona y el recipiente se empieza a mover.

En esta página, vamos a analizar un problema que comprende varias partes de la Física: la conservación del momento lineal, el balance energético, una transformación termodinámica, y nociones básicas de física estadística. Relacionaremos la temperatura del gas con la energía cinética media referida al c.m. de gas que se mueve.

Mecanismo básico

En primer lugar, vamos a estudiar el mecanismo básico. Un conjunto de N partículas que simulan un gas ideal bidimensional, está encerrado en un recipiente.

El usuario define el gas introduciendo los valores de

la masa de las partículas,
la velocidad media (proporcional a la raíz cuadrada de la temperatura)
el número total N de partículas.

Cuanto mayor es el número de partículas menor es el grado de fluctuación, aunque al programa interactivo le lleva más tiempo calcular las posiciones y velocidades de cada una de las partículas.

Cuando el recipiente está cerrado, las partículas chocan elásticamente con las cuatro paredes del recipiente. Si despreciamos las fluctuaciones, el recipiente no se mueve a consecuencia de los choques ya que la fuerza media sobre las paredes opuestas tiene el mismo módulo, la misma dirección y sentido contrario.

Choques entre las moléculas del gas y las paredes del recipiente.

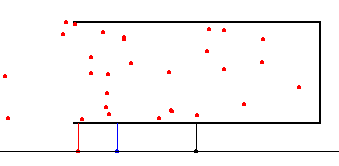Si eliminamos una de las paredes del recipiente. Los choques de las partículas con la pared opuesta hace que el recipiente se mueva. Sin embargo, el centro de masas del conjunto formado por el recipiente y el gas no cambia, por ser un sistema aislado inicialmente en reposo.

Podemos comprobar, que aproximadamente, un cuarto de las partículas se mueve en la dirección del eje X hacia la derecha y estas son las partículas que proporcionan momento lineal al recipiente.

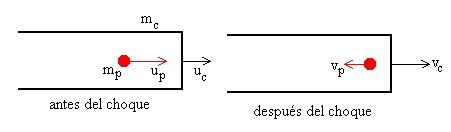
gas_1.gif (2139 bytes)

Sea m_p la masa de las partículas y u_p su velocidad antes del choque, y sea m_c la masa del recipiente y u_c su velocidad antes del choque. Las ecuaciones del conservación del momento lineal y de la energía cinética antes y después del choque elástico nos proporcionan dos ecuaciones de las cuales despejamos las velocidades v_p y v_c de de la partícula y del cilindro después del choque.

$v_{p} = \frac{2 m_{c} u_{c} + (m_{p} - m_{c}) u_{p}}{m_{p} + m_{c}} v_{c} = \frac{2 m_{p} u_{p} + (m_{c} - m_{p}) u_{c}}{m_{p} + m_{c}}$

Para simular las colisiones de las moléculas de un gas con las paredes del recipiente, se utiliza un modelo de gas ideal bidimensional. Dada la velocidad media de las moléculas del gas, el programa interactivo emplea los métodos de Montecarlo, para asignar un valor al módulo de la velocidad a cada una de las N moléculas de acuerdo con la fórmula de la distribución de velocidades. La dirección de la velocidad se asigna mediante un número aleatorio uniformemente distribuido en el intervalo 0- 2π .

Actividades

Se introduce

La masa del recipiente, m_cen el control de edición titulado Masa recipiente
La masa de cada partícula del gas, m_pen el control de edición titulado Masa partícula
La velocidad media de las partículas del gas, <v>, en el control de edición titulado Velocidad media p.
El número de partículas que componen el gas, N, en el control de edición titulado Número partículas

Se pulsa en el botón titulado Empieza.

Desaparece la tapa izquierda del recipiente. Se observa el movimiento de las partículas, su colisión con la pared derecha del recipiente y el movimiento del recipiente hacia la derecha con velocidad creciente.

El centro de masas del sistema formado por el gas y por el recipiente no cambia (sistema aislado).

Por la conservación del momento lineal a lo largo del eje X tendremos

m_g<v_g>+m_cv_c=0

donde m_g=N·m_p es la masa del gas, <v_g> su velocidad media a lo largo del eje X, (a lo largo del eje Y su velocidad media es cero), m_c es la masa del recipiente y v_c la velocidad del recipiente en un instante dado.

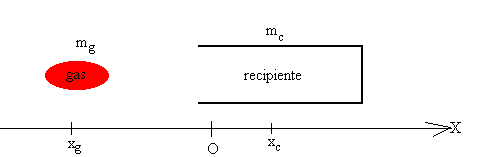
gas_2.gif (1971 bytes)

Si la masa del gas m_g es igual a la masa del recipiente m_c los centros de masas son equidistantes con la posición del c.m. del sistema aislado. Si son distintos las distancias son inversamente proporcionales a las masas

m_gx_g+m_cx_c=0

Análisis del problema

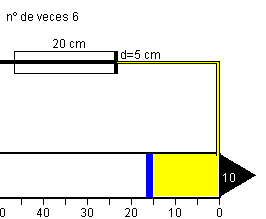Sea un cilindro de radio r y de longitud d, que tiene un émbolo fijado en la posición inicial z₀. Se llena de aire hasta una presión inicial p₀ mediante una bomba de bicicleta o dispositivo similar. Se suelta el émbolo y el gas se expande. Se trata de analizar el movimiento del cilindro en dos etapas distintas:

Durante la expansión (supuesta adiabática) del gas hasta que el émbolo sale del cilindro.
A continuación, el cilindro es empujado por los choques de las moléculas contra su pared izquierda.

Sistema aislado formado por tres componentes

Tenemos que estudiar un sistema aislado formado por tres componentes:

El cilindro de masa m_c
El gas contenido en el recipiente de masa m_g, que supondremos uniformemente distribuido en el volumen que ocupa.
El émbolo de masa m_e.

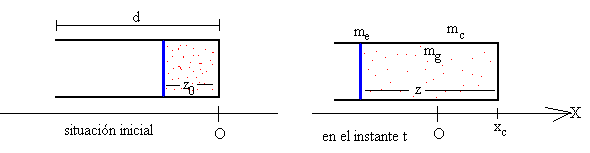
gas_3.gif (2673 bytes)

Comparamos la situación inicial a la izquierda de la figura (la posición del émbolo en el cilindro es z₀) , y la situación en el instante t en la que el émbolo se ha movido a la posición z en el interior del cilindro.

Podemos relacionar la posición z del émbolo en el interior del cilindro con la posición x_c del cilindro.

Calculemos la posición del c.m. del sistema aislado en el instante inicial y en el instante t.

$\begin{array}{l} x_{c m} = \frac{- m_{c} d / 2 - m_{e} z_{0} - m_{g} z_{0} / 2}{m_{c} + m_{e} + m_{g}} \\ x_{c m} = \frac{m_{c} (x_{c} - d / 2) + m_{e} (x_{c} - z) + m_{g} (x_{c} - z / 2)}{m_{c} + m_{e} + m_{g}} \end{array}$

El sistema aislado estaba inicialmente en reposo, su centro de masa no habrá cambiado de posición.

La relación entre la posición del cilindro x_c y la del émbolo z en el interior del cilindro es

$x_{c} = \frac{m_{e} + m_{g} / 2}{m_{e} + m_{g} + m_{c}} (z - z_{0})$

La velocidad del c.m. del sistema aislado es cero

$v_{c m} = \frac{m_{e} v_{e} + m_{g} v_{g} + m_{c} v_{c}}{m_{e} + m_{g} + m_{c}}$

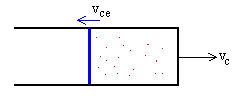gas_4.gif (1453 bytes) La velocidad del émbolo v_e es igual a la velocidad del cilindro v_c más la velocidad del émbolo respecto del cilindro v_ce.

v_e=v_c-v_ce

La velocidad del c.m. del gas es justamente la mitad de la velocidad del émbolo en el interior del cilindro, ya que si el émbolo se desplaza de z₀ a z en el tiempo t, el centro de masa del gas se desplaza de z₀/2 a z/2 en el mismo tiempo. Por tanto,

$v_{g} = v_{c} - \frac{v_{c e}}{2}$

Teniendo en cuenta que v_cm=0, relacionamos la velocidad del cilindro v_c con la velocidad del émbolo en el interior del cilindro v_ce.

$v_{c} = \frac{m_{e} + m_{g} / 2}{m_{e} + m_{g} + m_{c}} v_{c e}$

Como vemos es la misma relación que entre la posición x_c del cilindro y el desplazamiento del émbolo en el interior del cilindro z-z₀.

Expresamos las velocidades del émbolo v_e y del gas v_g en función de la velocidad del cilindro v_c, todas ellas medidas respecto del Sistema de Referencia del Laboratorio.

$v_{e} = - \frac{m_{g} + 2 m_{c}}{m_{g} + 2 m_{e}} v_{c} v_{g} = \frac{m_{e} - m_{c}}{m_{g} + 2 m_{e}} v_{c}$

Expansión adiabática del gas ideal

El cilindro está en el vacío, cerrado por un émbolo fijo situado en la posición z₀, se conecta a una bomba de bicicleta que tiene las siguientes dimensiones: 20 cm de largo y 5 cm de diámetro, su volumen en litros es V_b=π 0.05²·0.2·1000/4=0.393 l. Cada vez que se acciona la bomba se introducen en el cilindro n_b moles de gas

$n_{b} = \frac{p_{a t} V_{b}}{R T_{0}} n_{b} = 0 .016 moles$

La presión inicial del gas en el cilindro después de accionar N veces la bomba será

p₀V₀=( N·n_b)RT₀

Se libera el émbolo y el gas se expande muy rápidamente (supondremos una transformación adiabática), hasta que el émbolo alcanza la posición z=d, (se sale fuera del cilindro). El volumen final será por tanto

V=π r²d

Calculamos la presión final p y la temperatura final T.

Para un gas diatómico los calores específicos valen

c_v=5R/2, c_p=c_v+R=7R/2, índice adiabático γ =c_p/c_v=7/5.

gas_7.gif (2565 bytes) La presión final p se calcula a partir de la ecuación de la adiabática pV^γ =cte

$p_{0} V_{0}^{7 / 5} = p V^{7 / 5}$

la temperatura final se calcula a partir de p y V

$T = \frac{p V}{p_{0} V_{0}} T_{0}$

o bien, a partir de la ecuación de la adiabática expresada en términos de T y V.

$T_{0} V_{0}^{2 / 5} = T V^{2 / 5}$

Balance energético

Al expandirse adibáticamente el gas ideal su temperatura disminuye y por tanto, su energía interna también disminuye. Esta energía se convierte en energía cinética del cilindro, del émbolo y del centro de masas del gas.

La variación de energía interna ΔU de un gas ideal se calcula mediante la fórmula

ΔU=nc_v(T-T₀)

n es el número de moles del gas y c_v es el calor específico a volumen constante, y T-T₀ la variación de temperatura. Como T<T₀ la energía interna disminuye.

La expresión el balance energético del sistema aislado de tres componentes nos queda de la siguiente forma

$\begin{array}{l} n c_{v} (T - T_{0}) + \frac{1}{2} m_{c} v_{c}^{2} + \frac{1}{2} m_{e} v_{e}^{2} + \frac{1}{2} m_{g} v_{g}^{2} = 0 \\ n c_{v} (T_{0} - T) = \frac{1}{2} (m_{c} + m_{e} {(\frac{m_{g} + 2 m_{c}}{m_{g} + 2 m_{e}})}^{2} + m_{g} {(\frac{m_{e} - m_{c}}{m_{g} + 2 m_{e}})}^{2}) v_{c}^{2} \end{array}$

Si la masa del gas m_g es mucho más pequeña que la masa del émbolo m_e y del cilindro m_c esta expresión se simplifica

$n c_{v} (T_{0} - T) \approx \frac{1}{2} m_{c} (1 + \frac{m_{c}}{m_{e}}) v_{c}^{2}$

La velocidad del cilindro v_c es independiente del gas que lo contiene.

A partir de esta ecuación, calculamos la velocidad del cilindro v_c, la del émbolo v_e y la del c. m. del gas v_g.

Choque de las moléculas del gas con el cilindro.

Una vez que el émbolo sale del cilindro, las moléculas del gas chocan con la pared derecha del cilindro dándole un empuje adicional tal como hemos visto en la primer apartado de esta página.

La velocidad media de las moléculas del gas v_m está relacionada con su temperatura mediante la fórmula

$v_{m} = \sqrt{\frac{3 R T}{M}}$

donde M es la masa molecular del gas ideal.

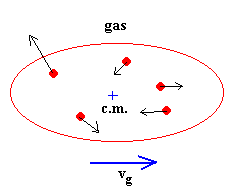gas_9.gif (1964 bytes) Supondremos que por término medio 1/6 de las moléculas se mueven a lo largo del eje X hacia la derecha con la misma velocidad v_m relativa al centro de masas del gas.

Las moléculas que chocan con la tapa derecha del cilindro tienen una velocidad v_m+v_g respecto del Sistema de Referencia del Laboratorio.

Si suponemos además, que el choque es elástico la velocidad final del cilindro v’_c será.

$v_{c}^{'} = \frac{2 \frac{1}{6} m_{g} (v_{m} + v_{g}) + (m_{c} - \frac{1}{6} m_{g}) v_{c}}{\frac{1}{6} m_{g} + m_{c}}$

Ejemplo

Supongamos que la posición inicial del émbolo z₀=15 cm, y que accionamos N=6 veces la bomba de bicicleta. Liberamos el émbolo de su posición inicial. Se pide calcular la velocidad del cilindro cuando el émbolo llega al final de su recorrido, y la velocidad final del cilindro teniendo en cuanta el impulso adicional debido al choque de las moléculas del gas con su tapa derecha.

Datos:

Las dimensiones del cilindro son: diámetro 10 cm, longitud 50 cm.
Las dimensiones de la bomba son 5 cm de diámetro y 20 cm de longitud.
La masa del émbolo m_e=0.3 kg
La masa del cilindro m_c=0.6 kg
La temperatura ambiente es de 27º C o de T₀=300 K.
Gases diatómicos

Gas Peso molecular M (g)

Helio 4.0

Neón 20.2

CO₂ 44.0

O₂ 32.0

N₂ 14.0

Calor específico a volumen constante c_v=5R/2
Constante de los gases R=0.082 atm·litro/(K·mol)=8.314 J/(K·mol)

Volumen de la bomba

V_b=π 0.05²·0.2·1000/4=0.393 l.

Número de moles de gas en la bomba

$n_{b} = \frac{p_{a t} V_{b}}{R T_{0}} n_{b} = 0 .016 moles$

Volumen inicial del cilindro

V₀=π r²z₀=π ·0.1²·0.15·1000/4=1.178 litros

Presión inicial p₀ del gas en el cilindro después de accionar N=6 veces la bomba

p₀V₀=(N·n_b)RT₀

p₀=2 atm

Expansión adiabática

$p_{0} V_{0}^{7 / 5} = p V^{7 / 5}$

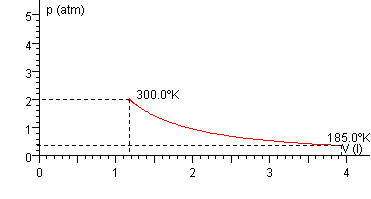
El volumen final es V=π r²d=π ·0.1²·0.5·1000/4=3.927 litros

La presión final p=0.371 atm, y la temperatura final T=185.3 K.

La variación de energía interna es

ΔU=nc_v(T-T₀)=0.096·(5/2)·8.314·(185.3-300)=-228. 9 J

Aplicando la ecuación del balance energético del sistema aislado de tres componentes, obtenemos la velocidad del cilindro.

La masa del gas es muy pequeña comparada con la masa del émbolo o del cilindro. La masa de Helio es m_g=n·M/1000=0.096·4/1000=3.832·10^-4 kg

$228.9 = \frac{1}{2} 1.8 v_{c}^{2} v_{c} = 15.93 m/s$

Velocidad del émbolo

$v_{e} = - \frac{m_{g} + 2 m_{c}}{m_{g} + 2 m_{e}} v_{c} v_{e} = - 31.85 m/s$

La velocidad del émbolo respecto del cilindro es v_ce=-31.85-15.93=-47.78 m/s

Velocidad del centro de masa del gas helio

$v_{g} = \frac{m_{e} - m_{c}}{m_{g} + 2 m_{e}} v_{c} v_{g} = - 7.97 m/s$

velocidad media de las moléculas de Helio

$v_{m} = \sqrt{\frac{3 R T}{M}} = \sqrt{\frac{3 \cdot 8.314 \cdot 185.3}{4 / 1000}} = 1075 m/s$

Esta velocidad es mucho mayor que la del c.m. del gas v_m>>v_g

Calculamos la velocidad final del cilindro

Suponiendo que 1/6 de las moléculas de helio chocan con la tapa derecha del cilindro. La velocidad de las moléculas es igual a la velocidad de su c.m. v_g más la velocidad v_m relativa al c.m. del gas.

$v_{c}^{'} = \frac{2 \frac{1}{6} m_{g} (v_{m} + v_{g}) + (m_{c} - \frac{1}{6} m_{g}) v_{c}}{\frac{1}{6} m_{g} + m_{c}} v_{c}^{'} = 16.15 m/s$

El tiempo que tardan en chocar todas las moléculas el gas con la tapa derecha del cilindro es

$t = \frac{d}{v_{m} + v_{g} - v_{c}}$

donde d es la longitud del cilindro, y el denominador es la velocidad de las moléculas relativa al cilindro.

t=4.76·10^-4 s

La velocidad con la que retroceden las moléculas del gas, se calcula mediante la fórmula

$v_{g}^{'} = \frac{2 m_{c} v_{c} + (\frac{1}{6} m_{g} - m_{c}) (v_{m} + v_{g})}{\frac{1}{6} m_{g} + m_{c}} v_{g}^{'} = - 1047.7 m/s$

Ejemplo:

Si elegimos CO₂, m_g=0.096·44/1000=4.215·10^-3 kg.

La velocidad del cilindro en el momento en que sale el émbolo es

v_c=15.96 m/s

Velocidad del émbolo

v_e=-31.81 m/s

La velocidad del émbolo respecto del cilindro es v_ce=-31.81-15.96=-47.77 m/s

En el caso del CO₂ la velocidad media de las moléculas del gas es más pequeña al ser mayor la masa de sus moléculas.

v_m=324.1 m/s.

La velocidad final del cilindro será

v’_c=16.66 m/s

La velocidad de retroceso del gas en su choque con la tapa derecha del cilindro es

v’_g=-296.3 m/s

Actividades

Se introduce

El gas diatómico en el control de selección titulado Gases
La masa del cilindro m_c,en el control de edición titulado Masa cilindro
La masa del émbolo m_e, en el control de edición titulado Masa émbolo
La posición inicial del émbolo z₀. actuando en la barra de desplazamiento titulada Pos. émbolo

Se pulsa el botón titulado Nuevo

Se pulsa varias veces el botón titulado Llenar gas, para llenar el cilindro de gas comprimido.

En la gráfica situada en la parte superior derecha del applet veremos un punto en el diagrama pV que señala la presión, el volumen y la temperatura inicial del gas en el recipiente.

Se pulsa el botón titulado Empieza.

El gas se expansiona adiabáticamente, podemos ver la transformación en el gráfico pV. También observamos cómo la temperatura disminuye. A su vez el émbolo y el cilindro se mueven en sentidos contrarios.

Cuando el émbolo sale del cilindro, el gas sigue empujándolo hasta que un sexto (en promedio) de las moléculas del gas han chocado con la tapa derecha del recipiente.

Apuntar los datos de la velocidad final del cilindro y compararlos con los cálculos realizados tomando como modelo el ejemplo.

Gas	Peso molecular M (g)
Helio	4.0
Neón	20.2
CO₂	44.0
O₂	32.0
N₂	14.0