| Orri honetan berriro kohetea aztertuko dugu, baina
oraingoan, Lurraren gainazaletik gorantz eta bertikalki jaurtitzen da.
Kohetea txikia dela suposatuko dugu (suziria) eta altuera txikia atzematen
duela, horrela grabitatearen azelerazioa konstantetzat har daiteke, g= 9.8
m/s2.
Kohetearen higidurak bi atal ezberdin izango ditu:
- Jaurtitzen denetik eta erregaia agortzen zaion arte.
- Erregaia agortzen den unetik altuera maximoa atzematen duen arte.
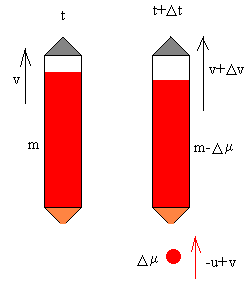 |
Demagun koheteak t aldiunean m masa duela
eta v abiadura, erreferentzia sistema inertzial batekiko
(esaterako Lurra). Ondorengo aldiunean, t+Δt,
erregaiaren zati bat egozten da, Δμ masaduna, eta -u
abiadura erlatiboaz kohetearekiko (abiadura hori konstantea da). Ondorioz,
kohetearen masa aldatzen da (m-Δμ) eta abiadura
ere bai, v+Δv. |
Koheteak t aldiunean m masa du eta v
abiadura, hortaz bere momentu lineala:
p(t)=mv
Ondorengo aldiunean, t+Δt:
-
Kohetearen masa da, m-Δμ, eta
bere abiadura, v+Δv.
-
Egotzitako zatiaren masa, Δμ, eta
abiadura erlatiboa –u da, kohetearekiko, alegia, –u+ v,
Lurrarekiko.
Momentu lineal totala une horretan:
p(t+Δt)=(m-Δμ)(v+Δv)+
Δμ(–u+ v+Δv)
Aldiune bien artean (t eta
t+Δt ) momentu lineala aldatu da, aldaketa hori honela idatz
daiteke:
Δp= p(t+Δt)-
p(t)=m·Δv- u·Δμ-Δμ·Δv
Eta limitean, denbora-tartea infinitesimala denean, Δt→0
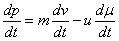
Baina momentu linealaren aldaketa, hain zuzen, kanpo indar
erresultantearen berdina da, izan ere, erakarpen grabitatorioa, eta beronek
momentu linealaren aurkako noranzkoa du:
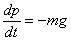
Bestalde, koheteak eta erregaiak osatutako multzoaren
M masa osoa konstantea da: m kohetearena eta μ
jaurtitako erregaiarena bada:
M=μ+m, eta beraz, dμ+dm=0. Kohetearen masa dm
gutxiagotzen bada, egotzitako erregaiaren masa kantitate berean handiagotzen
da, dμ=-dm.
Beraz, kohetearen higidura-ekuazioa honela idatz daiteke:
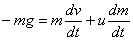
 |
Demagun erregaia erritmo konstanteaz egozten dela,
alegia, denbora unitateko erregai-kantitatea D= -dm/dt.
konstantea dela. Orduan, kohetearen masa denboraren menpe honela idatz
daiteke: m=m0 -D·t. Kohetearen hasierako masari m0
deitu diogu (masa erabilgarria gehi erregaia) eta hasieratik t
aldiunera arte egotzitako erregai-kantitatea D·t . 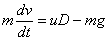
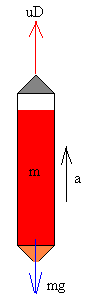
Kohete bat masa aldakorreko partikula gisa azter daiteke (m),
eta indar bi jasaten ditu, biak norabide berean baina aurkako
noranzkoez: gorantz gasen bultzada, uD, eta beherantz pisua mg. |
Kasu berezi gisa, urrutiko
espazioan zehar pisua nulua da, eta koheteak indar bakar bat jasaten du,
alegia, gasak erretzean eta jaurtitzean ematen dioten bultzada (uD).
Aurreko ekuazioa honela berridatz daiteke:
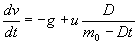
Eta ekuazio hori berehala integra daiteke:
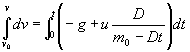
Eta horrek ematen du abiaduraren adierazpena denboraren menpe:
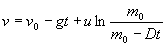
Berriz integratzen bada:
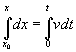
Kohetearen x posizioa lortzen da edozein aldiunetan:
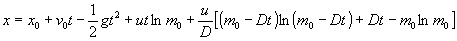
Gasen bultzada pisua baino handiagoa da
- Kohetearen erregai-kantitate totala: 1.0 kg
- Daraman karga erabilgarria: 2.0 kg
- Segundoro egotzitako erregai kantitatea: D=0.1 kg/s
- Gasen jaurtitze-abiadura erlatiboa: u=1000 m/s, kohetearekiko.
Kasu honetan, erregaia gordetzen duen ontzia edo depositua arbuiatuko
dugu.
- Koheteak jasaten dituen indarrak:
Kohetearen masa totala: karga erabilgarria + erregaia
m0=2.0+1.0=3.0 kg
Kohetearen pisua (m0·g =29.4 N) gasek
emandako bultzada baino txikiagoa da ( u·D=100 N)
- Erregaiak agortu arte irauten duen denbora:
Erregai-kantitate totala 1.0 kg denez, eta 0.1 kg/s-ko erritmoaz
erretzen denez, t0= 10 s. aldiunean agortuko da.
- Koheteak atzematen duen abiadura maximoa:
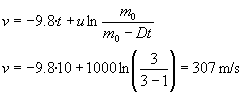
- Erregaia agortu arte atzematen duen altuera:
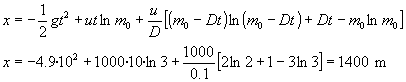
- Erregaia agortu ondoren, koheteak oraindik gorantz jarraitzen du,
baina abiadura moteltzen, altuera maximoa atzematen duen arte. Higiduraren
ekuazioak grabitate soilaren eraginpekoak dira:
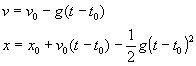
Hemen x0 eta v0 dira kohetearen
posizioa eta abiadura t0 aldiunean, justu erregaia
agortu denean.
Eta koheteak altuera maximoa atzematen du v=0 baldintza betetzen
duenean, alegia t=41.4 s. aldiunean. Kohetearen altuera aldiune
horretan hau da: x=6223 m.
Gasen bultzada pisua baino txikiagoa da
- Kohetearen erregai-kantitate totala: 2.0 kg
- Daraman karga erabilgarria: 9.0 kg
- Segundoro egotzitako erregai kantitatea: D=0.1 kg/s
- Gasen jaurtitze-abiadura: u=1000 m/s
Kasu honetan ere, erregaia gordetzen duen ontzia edo depositua arbuiatuko
dugu.
- Koheteak jasaten dituen indarrak
Kohetearen pisua ((2.0+9.0)·9.8=176.4 N) gasen bultzada baino handiagoa
da ( u·D=1000·0.1=100
N)
Kohetea ez da igotzen, eta geldi segitzen du, baina erregaia agortzen
doa, kohetearen pisua gutxitzen, harik eta kohetearen pisua eta gasen
bultzada berdintzen diren arte:
(c+9)·9.8=100
Hortik c kalkulatzen da. Kohetea gorantz mugitzen hasiko da erregai-kantitatea hau denean, c=1.204 kg. Hortaz erregaiaren kantitate bat alferrik galdu da,
izan ere, 2-1.204=0.796 kg.
- Koheteak, gorantz abiatzen denean, duen masa:
m0= 1.204+9.0=10.204 kg
- Erregaiak agortu arte irauten duen denbora:
1.204 kg erregai dituenez, eta 0.1 kg/s-ko erritmoaz jaurtitzen denez,
erregaia agortuko da 12.04 s. aldiunean.
- Koheteak atzematen duen abiadura maximoa:
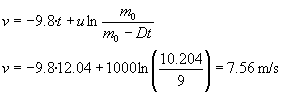
- Erregaia agortu arte atzematen duen altuera:
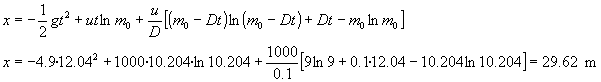
- Altuera maximoa atzematen duen arte iragandako denbora:
0=7.56-9.8(t-12.04)
t=12.8 s
Kohetearen altuera aldiune horretan.
x=29.62+7.56·0.77-4.9·0.772=32.5 m
Aukeran idatz daitezke:
- Kohetearen hasierako erregaia, kg-tan (<2kg).
- Koheteak duen Karga erabilgarria, kg-tan (<10kg).
- Segundoro xahututako erregai kantitatea, D, kg/s-tan
(<1kg/s).
Gasen abiadura erlatiboa kohetearekiko finkotzat hartu da: u=1000m/s.
Hasi botoia sakatu.
Leihatilan kohetea ikusten da, atzeko aldetik gasak jaurtitzen.
Alboan gezi bi adierazten dira: gorriak gasen bultzada adierazten du, eta
urdinak pisua. Gasen bultzada konstantea da erregaia agortzen den arte,
pisua ordea, gutxitzen doa erregaia jaurtitzen ari delako.
Kohetearen hasierako pisua (karga erabilgarria gehi erregaia, m0·g),
gasek ematen dioten bultzada baino handiagoa bada (u·D), orduan
kohetea ez da igotzen eta geldi mantentzen da, baina erregaia agortzen doa,
kohetearen pisua gutxitzen, harik eta gasen bultzada
berdintzen duen arte.
Kohetea gorantz abiatzen den unetik aurrera, erregaia xahutzen segitzen
du erabat agortzen duen arte. Erregaia agortzen den aldiunea kalkulatzeko
zatitu behar da, koheteak daukan erregai-kantitatea zati segundoro xahutzen
duena.
Koheteak atzematen duen abiadura maximoa, erregaia agortzen den
aldiunean:
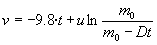
hemen m0 da, kohetearen masa, mugitzen hasi denean, eta t
denbora, kohetea abiatzen denetik erregaia agortu artekoa. Ondoren koheteak
gorantz igotzen segitzen du, abiadura motelduz, altuera maximoa atzematen
duen arte, alegia, bere abiadura anulatzen den arte.
- Leihatilaren eskumako aldean grafiko batek abiadura adierazten du
denboraren menpe.
- Leihatilaren ezkerreko aldean, partikula gorri txiki batez, kohetea
bera adierazten da bere altuera behatzeko denboraren menpe.
|