| Aurreko orri batean material baten elastikotasun-modulua (edo Young-en
modulua) neurtu dugu, materialari trakzio-esfortzu bat aplikatuz eta
bere luzapena neurtuz. Oraingoan, materialari tortsio- edo
ebakidura-esfortzu bat aplikatuko diogu eta deformazioa neurtuko dugu.
Horrelako esfortzu batean materialaren bolumena ez da aldatzen baina
bihurritu egiten da. Ebakidura-moduluari G deritzo eta material
bakoitzaren berezitasuna da.
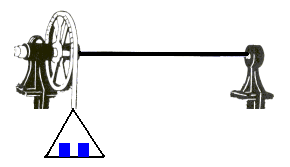 |
Irudiko tresna esperimentalak material
jakin baten hagatxo bat bihurritzen du. Hagatxoaren luzera eta lodiera
aldakorrak izan daitezke. Hagatxoaren mutur bat tinko mantentzen da
(eskumakoa) eta bestea polea batean lotzen da (ezkerrekoa). Poleari soka
bat lotzen zaio eta soka horretan pisuak eskegitzen dira, hagatxoa
bihurrituz. Eskala angeluar batek hagatxoaren bihurritzea
neurtzen du, alegia, M momentuak eraginda, hagatxoaren ezkerreko
muturrak biratzen duen q angelua. |
Demagun gorputz solido batek paralelepipedo bat osatzen duela: S
oinarria eta h altuera.
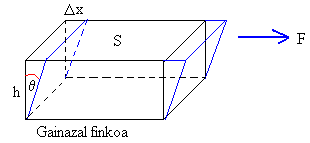 |
Gorputz horri gaineko aldean F indar horizontal
bat aplikatzen bazaio, irudiak erakusten duena bezalakoa, eta bitartean
azpiko aldeari tinko eusten bazaio, gorputzari eragiten zaion
deformazioari ebakidura deritzo. Deformazio-mota horretan gorputzaren
bolumena ez da aldatzen, baina forma bai. Hasieran, gorputzaren sekzioa
laukizuzena da eta deformatu ondoren, paralelogramoa da. |
Esfortzua definitzen da, indar tangentziala zati aplikatzen den aldearen
azalera: F/S. Eta deformazioa definitzen da, gaineko aldearen
desplazamendu horizontala zati gorputzaren altuera: Dx/h
(ikusi irudia). G ebakidura-modulua da, esfortzua zati deformazioa,
eta material ezberdinek ebakidura-modulu ezberdinak dituzte, bere
gogortasunaren arabera.
Materiala gogorra bada, desplazamendua txikia izango da, eta orduan
honako erlazioa idatz daiteke:
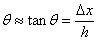
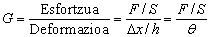
|
Metala |
Ebakidura-modulua, G,
×109 N/m2 |
| Kobrea,
hotzean tenkatua |
48.0 |
| Aluminioa |
25.0-26.0 |
| Altzairua, karbonoduna |
8 |
| Altzairua, aleatua |
80.0 |
| Zink, laminatua |
31.0 |
| Letoia,
hotzean tenkatua |
34.0-36.0 |
| Letoia, itsas laminatua |
36.0 |
| Brontzea, aluminioduna |
41.0 |
| Titanioa |
44.0 |
| Nikela |
79.0 |
| Zilarra |
30.3 |
Iturria: Koshkin N. I., Shirkévich M.G.. Manual de Física. Mir
argitaletxea
(1975)
Har dezagun material zilindriko bat R erradioduna eta L
luzeraduna. Zilindroaren goiko muturrari tinko eusten diogu, eta behekoari indar
bat aplikatzen diogu zilindroa bihurritzeko norabidean. Irudiak erakusten
duenez, zilindroaren ardatzak eta erradioak laukizuzen bat osatzen dute
(urdina), eta bihurritzerakoan laukizuzena paralelogramo bilakatu da.
Deformazioa j angelua da.
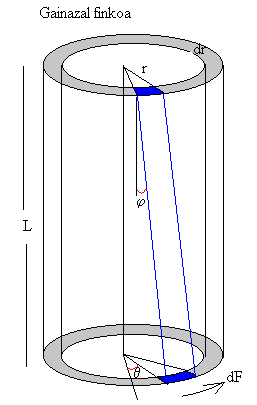 |
dF indarra aplikatzen da eraztun formako
gainazal batean (gris kolorekoa) r erradioa eta dr
lodiera ditu eta, beraz, bere azalera hau da: 2pr·dr. G
ebakidura-modulua da, esfortzua zati deformazioa. Esfortzua da, indar
tangentziala zati
azalera: F/S, eta deformazioa j
angelua da.
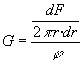
Irudiak erakusten duenez, deformazioaren j
angelua eta desplazamenduaren q
angelua erlazionatuta daude: Lj =rq . |
Aplikatutako
indarraren momentua:
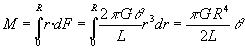
Ikusten denez, aplikatutako indarraren momentua (M) mutur askearen
bihurritzearen proportzionala da (q).
Formula horri esker, zilindroaren R erradioa eta L luzera
ezagututa, materialaren G ebakidura-modulua kalkulatu ahal izango
dugu.
Adibidea:
Demagun aluminiozko habe bat:
- L=100 cm edo 1.0 m-ko luzera.
- R=3.2 mm edo 0.0032 m-ko erradioa.
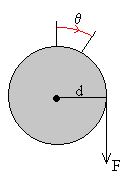 |
Poleatik pasatzen den sokan pisua eskegitzen dugu: 1250
g, eta horren ondorioz zilindroaren bihurritze-angelua hau da: 11.9
gradu. Bi datu horiekin aluminioaren G ebakidura-modulua kalkula
daiteke: Aplikatutako indarraren momentua hau da: M=F·d=1.25·9.8·0.07=0.8575
N·m
Eta biratutako angelua, radianetan: q =11.9·p /180=0.208 rad |
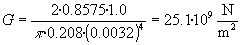
Aukeran idatz daiteke:
- Hagatxoaren luzera, cm-tan.
- Hagatxoaren erradioa, mm-tan.
- Hagatxoa osatzen duen materiala.
- Polearen erradioa finkoa da: d=7 cm
- Pisu-mota aukeratzen da: 100 g, 250 g edo 500 g dagokion botoia
aktibatuz.
Berria botoia sakatu.
- Saguarekin, pisua hartu eta sokaren mutur askean eskegi arte eramaten
da.
- Hagatxoaren bihurritzea neurtzen da, alboko eskalan (gradutan).
- Beste pisu bat hartu eta lehenagoko pisuaren azpian eskegitzen da.
Leihatilaren ezkerreko aldean, datu-bikoteak idatzita agertzen dira: masa
(kg-tan) eta biratutako angelua (gradutan). Datu-kopuru nahikoa bildu
direnean Grafikoa botoia sakatuz programak datuok grafikoki
adierazten ditu. Puntu esperimentalek zuzen bat osatzen dute, programak
zuzen horren ekuazioa kalkulatzen du eta maldaren balioa idatziz ematen du,
a, gradu/kg unitateetan.
Maldaren zenbakizko balioarekin, eta hagatxoaren neurriekin, materialaren G
ebakidura-modulua kalkula daiteke.
Adibidea:
- Aluminiozko hagatxoa.
- Luzera: L=1.0 m
- Sekzio zirkularraren erradioa: R=0.0032 m
- Polearen erradioa: d=7 cm=0.07 m
- Grabitatearen azelerazioa: g=9.8 m/s2
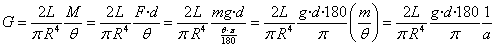
Esaterako, zuzenaren maldak ematen badu: a=9.55 (gradu/kg), orduan
aluminioaren ebakidura-modulua hau da: G=25.0·109 N/m2
Lortutako emaitza egiaztatzeko, esperimentua, eta kalkulua, burutu
ondoren, Erantzuna botoia sakatu, eta programak material horren G
ebakidura-modulua ematen du. |