Movimiento curvilíneo (II)
21.- Se disparan proyectiles con velocidad inicial de v 0 =8 m/s en todas las direcciones 0<θ <π/2 desde un punto P situado a h 1 =0.6 m por debajo del techo y h 2 =3 m por encima del suelo. Los proyectiles que llegan al techo rebotan elásticamente. Cuando llegan al suelo las colisiones son completamente inelásticas.
Determinar el ángulo crítico de disparo θm para la trayectoria justamente roze con el techo
Determinar el punto de impacto en el suelo de un proyectil cuyo ángulo de tiro θ <θm
Determinar el punto de impacto en el suelo de un proyectil cuyo ángulo de tiro θ >θm
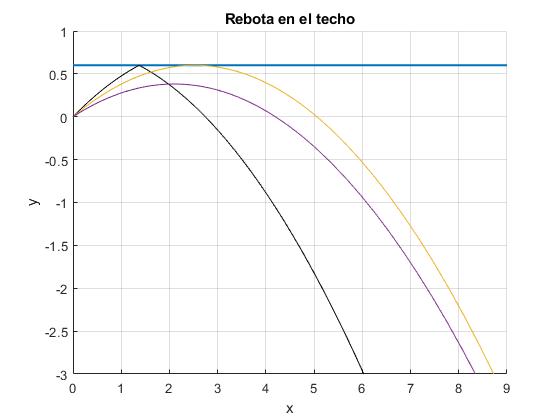
En color amarillo, la trayectoria correspondiente al ángulo crítico de disparo, θm
Physics Challenge for Teachers and Students. A
fall with a bang . The Physics Teacher, Vol. 58. September 2020, pp. 443 Solution to the September, 2020 Challenge . Phys. Teach. 58, A686 (2020)
Solución
La ecuaciones del movimiento de un proyectil disparado desde el origen con velocidad v 0 haciendo un ángulo θ es
{
a
x
= 0
a
x
= − g
{
v
x
=
v
0
cos θ
v
y
=
v
0
sin θ − g t
{
x =
v
0
cos θ · t
y =
v
0
sin θ · t −
1
2
g
t
2
Angulo crítico θm
La componente vertical vy de la velocidad cuando el proyectil llega al techo y=h 1 es nula
{
0 =
v
0
sin θ − g
t
1
h
1
=
v
0
sin θ ·
t
1
−
1
2
g
t
1
2
sin
θ
m
=
2 g
h
1
v
0
con h 1 =0.6 m y v 0 =8 m/s, obtenemos θm =25.38°
El proyectil impacta en el suelo y=-h 2 en la posición
−
h
2
=
v
0
sin
θ
m
· t −
1
2
g
t
2
t =
v
0
sin
θ
m
+
v
0
2
sin
2
θ
m
+ 2 g
h
2
g
x =
v
0
cos
θ
m
· t
Obtenemos t =1.207 s y x =8.724 m
Angulo θ<θm , por ejemplo θ =π/9 (20°)
El tiempo que tarda en llegar al suelo y=-h 2 y la posición del punto de impacto son
{
x =
v
0
cos θ · t
−
h
2
=
v
0
sin θ · t −
1
2
g
t
2
t =
v
0
sin θ +
v
0
2
sin
2
θ + 2 g
h
2
g
x =
v
0
cos θ · t
Obtenemos, t =1.110 s y x =8.344 m
Angulo θ>θm , por ejemplo θ =π/3 (30°)
El proyectil llega al techo en el instante t 1
h
1
=
v
0
sin θ ·
t
1
−
1
2
g
t
1
2
t
1
=
v
0
sin θ −
v
0
2
sin
2
θ − 2 g
h
1
g
La posición del punto de impacto en el techo y=h 1 es x 0 =v 0 cosθ ·t 1
Las componentes de la velocidad del proyectil en este instante t 1 son
{
v
0 x
=
v
0
cos θ
v
0 y
=
v
0
sin θ − g
t
1
Si el choque contra el techo es elástico, la componente vertical de la velocidad vy cambia de sentido
{
v
0 x
=
v
0
cos θ
v
0 y
= −
v
0
sin θ + g
t
1
Las ecuaciones del movimiento del proyectil desde el punto de partida en el techo hasta que llega al suelo son
{
x =
x
0
+
v
0 x
· t
y =
h
1
+
v
0 y
t −
1
2
g
t
2
Llega al suelo y=-h 2 en el instante t 1 +t 2 tal que
−
h
2
=
h
1
+
v
0 y
t
2
−
1
2
g
t
2
2
t
2
=
v
0 y
+
v
0 y
2
+ 2 g (
h
1
+
h
2
)
g
El punto de impacto en el suelo y=-h 2 es x=x 0 +v 0x ·t 2
El tiempo desde que parte del techo y llega al suelo, t 2 =0.672 s, el punto de impacto en el suelo, x =6.031 m
El código para representar las tres trayectorias es
h1=0.6; %posición del techo
h2=3; %posición del suelo
v0=8; %velocidad inicial
th_m=asin(sqrt(2*9.8*h1)/v0); %ángulo crítico
hold on
line([0,9],[h1,h1],'lineWidth',1.5) %techo
th=pi/6; %choca con el techo
t1=(v0*sin(th)-sqrt(v0^2*sin(th)^2-2*9.8*h1))/9.8; %llega al techo
x=@(t) v0*cos(th)*t;
y=@(t) v0*sin(th)*t-4.9*t.^2;
fplot(x,y,[0,t1],'color','k');
v0x=v0*cos(th);
v0y=-v0*sin(th)+9.8*t1; %cambia de sentido de la vy
t2=(v0y+sqrt(v0y^2+2*9.8*(h1+h2)))/9.8; %llega al suelo
x=@(t) v0*cos(th)*t1+v0x*t;
y=@(t) h1+v0y*t-4.9*t.^2;
fplot(x,y,[0,t2],'color','k');
for th=[th_m,pi/9]
x=@(t) v0*cos(th)*t;
y=@(t) v0*sin(th)*t-4.9*t.^2;
t2=(v0*sin(th)+sqrt(v0^2*sin(th)^2+2*9.8*h2))/9.8;
fplot(x,y,[0,t2]);
end
hold off
xlabel('x')
ylabel('y')
grid on
title('Rebota en el techo')
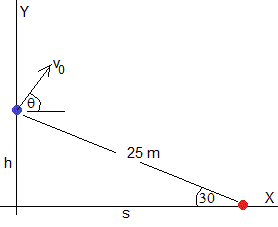
22.- En el instante t =0 se dispara un proyectil con velocidad v 0 , haciendo un ángulo θ 1 con la horizontal, desde un punto situado a una altura h por encima del origen.
Un segundo más tarde, se dispara otro proyectil con la misma velocidad v 0 , haciendo un ángulo θ 2 con la horizontal, desde el mismo punto situado a la misma altura h por encima del origen.
Ambos proyectiles llegan simultáneamente al mismo punto de impacto situado a una distancia s del origen.
Suponiendo que la distancia entre las posiciones de disparo y de impacto es r =25 m, calcular el tiempo de vuelo T de primer proyectil
Physics Challenge for Teachers and Students. Second to one . Phys. Teach. 60, 520 (2022)
Solución
Las ecuaciones del tiro parabólico son
{
x =
v
0
cos θ t
y = h +
v
0
sin θ t −
1
2
g
t
2
El primer proyectil tarda T en llegar al punto de impacto
{
s =
v
1 x
T ,
v
1 x
=
v
0
cos
θ
1
0 = h +
v
1 y
T −
1
2
g
T
2
,
v
1 y
=
v
0
sin
θ
1
El segundo proyectil tarda T -1 en llegar al punto de impacto
{
s =
v
2 x
(
T − 1
) ,
v
2 x
=
v
0
cos
θ
2
0 = h +
v
2 y
(
T − 1
) −
1
2
g
(
T − 1
) 2
,
v
2 y
=
v
0
sin
θ
2
Como las velocidades de disparo son iguales a v 0 , se cumplirá que
v
1 x
2
+
v
1 y
2
=
v
2 x
2
+
v
2 y
2
Despejamos v1x , v1y , v2x y v2y y los introducimos en la última ecuación
s
2
T
2
+
(
1
2
g
T
2
− h
)
2
T
2
=
s
2
(
T − 1
)
2
+
(
1
2
g
(
T − 1
)
2
− h
)
2
(
T − 1
)
2
1
4
g
2
T
4
+
h
2
+
s
2
− g h
T
2
T
2
=
1
4
g
2
(
T − 1
)
4
+
h
2
+
s
2
− g h
(
T − 1
)
2
(
T − 1
)
2
(
1
4
g
2
T
4
+
r
2
− g h
T
2
)
(
T − 1
) 2
= (
1
4
g
2
(
T − 1
)
4
+
r
2
− g h
(
T − 1
)
2
)
T
2
1
4
g
2
T
4
(
T − 1
) 2
−
1
4
g
2
(
T − 1
) 4
T
2
+
r
2
(
T − 1
) 2
−
r
2
T
2
= 0
(
2 T − 1
)
1
4
g
2
T
2
(
T − 1
) 2
− (
2 T − 1
)
r
2
= 0
T
2
(
T − 1
) 2
=
4
r
2
g
2
Solamente, una de las raíces de la ecuación de segundo grado es válida
T
2
− T −
2 r
g
= 0, T =
1 +
1 +
8 r
g
2
=
1 +
21
2
s
Conocido el tiempo de vuelo T , las componentes de la velocidad de disparo v 0 son
v
1 x
=
s
T
,
v
1 y
=
1
2
g
T
2
− h
T
=
1
2
g T −
h
T
v
2 x
=
s
T − 1
,
v
2 y
=
1
2
g (
T − 1
) −
h
T − 1
Conocidas las componentes de la velocidad de disparo v 0 , los ángulos de tiro son
tan
θ
1
=
v
1 y
v
1 x
, tan
θ
2
=
v
2 y
v
2 x
s=25*cosd(30); %posición del disparo
h=25*sind(30);
T=(1+sqrt(21))/2;
v1x=s/T; %componentes de la velocidad de disparo
v1y=5*T-h/T;
v2x=s/(T-1);
v2y=5*(T-1)-h/(T-1);
x=@(t) v1x*t; %ecuación del primer proyectil
y=@(t) v1y*t-5*t.^2;
hold on
fplot(x,y,[0,T])
x=@(t) v2x*t; %ecuación del segundo proyectil
y=@(t) v2y*t-5*t.^2;
fplot(x,y,[0,T-1])
hold off
grid on
xlabel('x (m)')
ylabel('y (m)')
title('Tiro parabólico')
Los ángulos de tiro son θ 1 =50.7°, θ 2 =9.3°
>> atand(v1y/v1x)
ans = 50.7048
>> atand(v2y/v2x)
ans = 9.2952
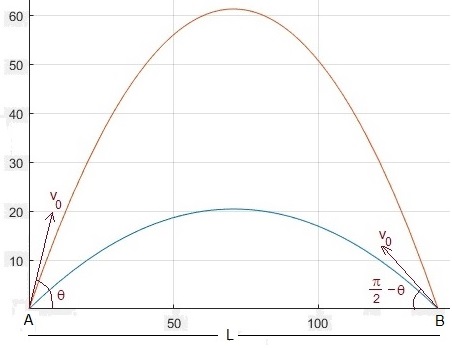
23.- Dos puntos A y B situados en el plano horizontal distan L . Se dispara un proyectil desde A con velocidad v 0 haciendo un ángulo θ con la horizontal. Simultáneamente, se dispara otro proyectil desde B con la misma velocidad haciendo un ángulo π/2-θ con la horizontal.
Calcular la distancia mínima entre los dos proyectiles
Physics Challenge for Teachers and Students. The Meeting Is Canceled (F1) . Phys. Teach. 43, February 2005, pp. 122
Solución
Las ecuaciones del movimiento de un proyectil disparado con velocidad v 0 haciendo un ángulo θ con la horizontal
{
x =
v
0
cos θ · t
y =
v
0
sin θ · t −
1
2
g
t
2
Llega al punto de impacto y =0, en el instante T (tiempo de vuelo) y su alcance L
T =
2
v
0
sin θ
g
L =
v
0
cos θ T =
v
0
2
sin (
2 θ
)
g
Los proyectiles disparados desde A (con ángulo θ ) o desde B (con ángulo π/2-θ ) tienen el mismo alcance L por tanto, el punto de disparo de uno es el de impacto del otro y viceversa.
Proyectil disparado desde el origen A con velocidad v 0 y ángulo θ
{
x
A
=
v
0
cos θ · t
y
A
=
v
0
sin θ · t −
1
2
g
t
2
Proyectil disparado desde B con velocidad v 0 y ángulo π/2-θ
{
x
B
= L −
v
0
sin θ · t
y
B
=
v
0
cos θ · t −
1
2
g
t
2
Distancia entre los dos proyectiles en el instante t
d
→
= (
x
B
−
x
A
)
i
^
+ (
y
B
−
y
A
)
j
^
d
2
=
(
x
B
−
x
A
) 2
+
(
y
B
−
y
A
) 2
=
(
L −
v
0
sin θ · t −
v
0
cos θ · t
) 2
+
(
v
0
cos θ · t −
1
2
g
t
2
−
v
0
sin θ · t +
1
2
g
t
2
) 2
=
(
L −
v
0
(
sin θ + cos θ
) t
) 2
+
(
v
0
(
cos θ − sin θ
) t
) 2
d
2
=
L
2
− 2 L
v
0
(
sin θ + cos θ
) t + 2
v
0
2
t
2
El tiempo mínimo se obtiene, derivando con respecto del tiempo t e igualando a cero
d (
d
2
)
d t
= 4
v
0
2
t − 2 L
v
0
(
sin θ + cos θ
) = 0
t
m
=
L (
sin θ + cos θ
)
2
v
0
La distancia mínima dm en el instante tm es
d
m
2
=
L
2
− 2 L
v
0
(
sin θ + cos θ
)
L (
sin θ + cos θ
)
2
v
0
+ 2
v
0
2
(
L (
sin θ + cos θ
)
2
v
0
) 2
=
L
2
−
L
2
(
sin θ + cos θ
) 2
+
1
2
L
2
(
sin θ + cos θ
) 2
=
L
2
−
1
2
L
2
(
sin θ + cos θ
) 2
d
m
2
=
L
2
2
(
1 − sin (
2 θ
)
)
d
m
= L
1 − sin (
2 θ
)
2
=
v
0
2
sin (
2 θ
)
g
1 − sin (
2 θ
)
2
v0=40; %velocidad de disparo
th=pi/6;%ángulo de tiro
x=@(t) v0*cos(th)*t;
y=@(t) v0*sin(th)*t-4.9*t.^2;
T=v0*sin(th)/4.9; %tiempo de vuelo
L=v0^2*sin(2*th)/9.8; %alcance
hold on
fplot(x,y,[0,T])
th=pi/2-th;
xx=@(t) L-v0*cos(th)*t;
yy=@(t) v0*sin(th)*t-4.9*t.^2;
T=v0*sin(th)/4.9; %tiempo de vuelo
fplot(xx,yy,[0,T])
tm=L*(cos(th)+sin(th))/(2*v0);
line([x(tm),xx(tm)],[y(tm),yy(tm)],'lineStyle','--')
plot(x(tm),y(tm),'ro','markersize',3,'markerfacecolor','r')
plot(xx(tm),yy(tm),'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
xlabel('x (m)')
ylabel('y (m)')
title('Tiro parabólico')

 Solución
Solución