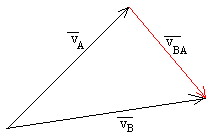
Problemas de Cinemática
Movimiento rectilíneo
Se denomina movimiento rectilíneo, aquél cuya trayectoria es una línea recta.

En la recta situamos un origen O, donde estará un observador que medirá la posición del móvil x en el instante t.
| Posición | x(t) |
| Velocidad | |
| Aceleración |
Dada la velocidad v(t) calcular el desplazamiento del móvil x-x0 del móvil entre los instantes t0 y t.
Dada la aceleración a(t) calcular el cambio de velocidad v-v0 que experimenta el móvil entre los instantes t0 y t
Movimiento rectilíneo uniforme
Un movimiento rectilíneo uniforme es aquél cuya velocidad es constante, por tanto, la aceleración es cero.
Movimiento rectilíneo uniformemente acelerado
Un movimiento uniformemente acelerado es aquél cuya aceleración es constante.
Despejando el tiempo t en la segunda ecuación y sustituyéndola en la tercera, relacionamos la velocidad v con el desplazamiento x-x0
Caída de los cuerpos
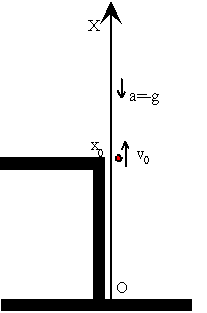
Un cuerpo es lanzado desde el techo de un edificio de altura x0 con velocidad v0, escribir las ecuaciones del movimiento, calcular la altura máxima y el tiempo que tarda el cuerpo en alcanzar el origen.
En primer lugar, establecemos el origen y la dirección del movimiento, el eje X. Después, los valores de la posición inicial y los valores y signos de la velocidad inicial, y de la aceleración, tal como se indica en la figura. Resultando las siguientes ecuaciones del movimiento.
Cuando alcanza la altura máxima, la velocidad del móvil es cero.
El tiempo que tarda en llegar al suelo, se obtiene a partir de la ecuación de la posición, poniendo x=0
Movimiento curvilíneo
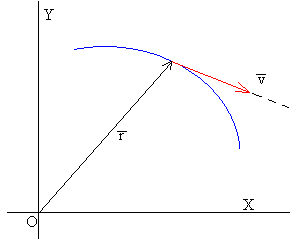
Para describir un movimiento que tiene lugar en el plano XY, situamos un origen y unos ejes.
En la figura se señala el vector posición del móvil en el instante t y el vector velocidad , cuya dirección es tangente a la trayectoria.
| Vector posición | x(t) | y(t) |
| Vector velocidad | ||
| Vector aceleración |
Podemos considerar un movimiento curvilíneo como la composición de movimientos rectilíneos a lo largo de los ejes coordenados.
Componentes tangencial y normal de la aceleración
Para calcular las componentes tangencial y normal de la aceleración en un determinado instante:
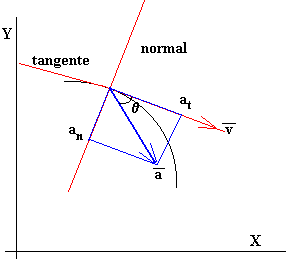
Se dibujan los ejes horizontal X y vertical Y.
Se calculan las componentes rectangulares de la velocidad y de la aceleración en dicho instante. Se representan los vectores velocidad y aceleración en dicho sistema de referencia.
Se dibujan los nuevos ejes, la dirección tangencial es la misma que la dirección de la velocidad, la dirección normal es perpendicular a la dirección tangencial.
Con la regla y el cartabón se proyecta el vector aceleración sobre la dirección tangencial y sobre la dirección normal.
Se determina el ángulo θ entre el vector velocidad y el vector aceleración, y se calcula el valor numérico de dichas componentes: at=a cosθ y an=a sinθ
Tiro parabólico
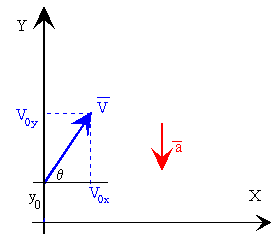
Un proyectil se dispara con velocidad inicial v0, haciendo un ángulo θ con la horizontal, las componentes de la velocidad inicial son
El tiro parabólico es la composición de dos movimientos:
- movimiento rectilíneo y uniforme a lo largo del eje X
- uniformemente acelerado a lo largo del eje Y
Las ecuaciones del movimiento de un proyectil bajo la aceleración constante de la gravedad son:
Movimiento circular
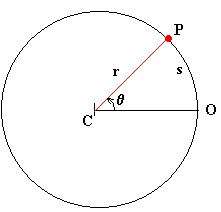
Se define movimiento circular como aquél cuya trayectoria es una circunferencia. Una vez situado el origen O de ángulos describimos el movimiento circular mediante las siguientes magnitudes.
En el instante t el móvil se encuentra en el punto P. Su posición angular viene dada por el ángulo θ, que hace el punto P, el centro de la circunferencia C y el origen de ángulos O.
| Posición angular | θ(t) |
| Velocidad angular | |
| Aceleración angular |
Dada la velocidad angular ω(t) calcular el desplazamiento del móvil θ-θ0 del móvil entre los instantes t0 y t.
Dada la aceleración angular α(t) calcular el cambio de velocidad ω-ω0 que experimenta el móvil entre los instantes t0 y t
Movimiento circular uniforme
Un movimiento circular uniforme es aquél cuya velocidad es constante, por tanto, la aceleración es cero.
Movimiento circular uniformemente acelerado
Un movimiento circular uniformemente acelerado es aquél cuya aceleración es constante.
Relación entre las magnitudes lineales y angulares.
La relación entre las magnitudes angulares y lineales es la siguiente:
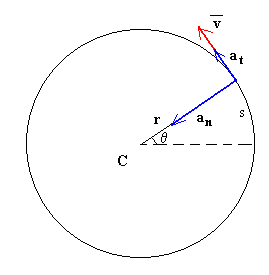
Longitud del arco s=r·θ
Velocidad, v=ω·r. La dirección de la velocidad de un móvil que describe un movimiento circular es tangente a la trayectoria circular.
Un móvil tiene aceleración tangencial at=α·r siempre que cambie el módulo de la velocidad con el tiempo. El sentido de la aceleración tangencial es el mismo que el de la velocidad si el móvil acelera y es de sentido contrario, si se frena. Un móvil que describe un movimiento circular uniforme no tiene aceleración tangencial.
Un móvil que describe un movimiento circular siempre tiene aceleración normal, an=ω2r ya que cambia la dirección de la velocidad con el tiempo. La aceleración normal tiene dirección radial y sentido hacia el centro de la circunferencia que describe.
La aceleración del móvil se obtiene sumando vectorialmente ambas componentes de la aceleración.
Movimiento relativo de traslación uniforme