Ecuaciones del movimiento

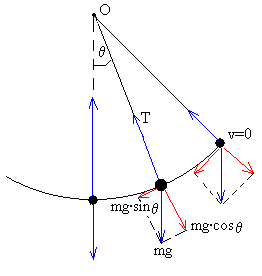
Si la partícula se desplaza a una posición θ₀ (ángulo que hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar.

El péndulo describe una trayectoria circular, un arco de una circunferencia de radio l. Estudiaremos su movimiento en la dirección tangencial y en la dirección normal.

Las fuerzas que actúan sobre la partícula de masa m son dos

• el peso mg
• La tensión T del hilo

Ecuación del movimiento en la dirección radial

La aceleración de la partícula es a_n=v²/l dirigida radialmente hacia el centro de su trayectoria circular.

La segunda ley de Newton se escribe

ma_n=T-mg·cosθ

Conocido el valor de la velocidad v en la posición angular θ determinamos la tensión T del hilo, (véase el apartado conservación de la energía)

La tensión T del hilo es máxima, cuando el péndulo pasa por la posición de equilibrio, T=mg+mv²/l

Es mínima, en los extremos de su trayectoria cuando la velocidad es cero, T=mgcosθ₀

Ecuación del movimiento en la dirección tangencial

La aceleración de la partícula es a_t=dv/dt.

La segunda ley de Newton se escribe

ma_t=-mg·sinθ

La relación entre la aceleración tangencial a_t y la aceleración angular α es a_t=α·l. La ecuación del movimiento se escribe en forma de ecuación diferencial

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{g}{l}\sin \theta =0}$

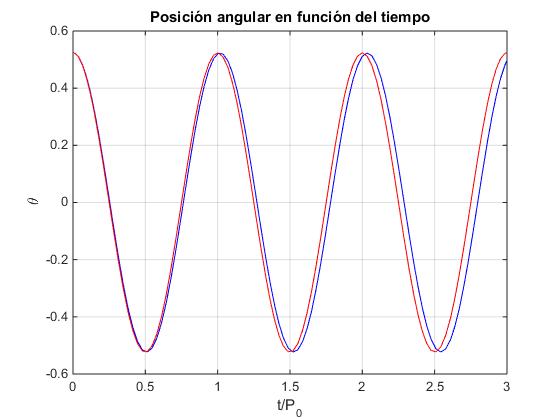
Solución numérica

Escribimos la ecuación diferencial del movimiento en términos de la variable adimensional τ=t/P₀. Donde P₀ es el periodo del las oscilaciones cuando la amplitud es pequeña (véase más abajo)

${\displaystyle \begin{array}{l}{P}_0=2\pi \sqrt{\frac{l}{g}}\\ \frac{d^2\theta }{d{t}^2}+4{\pi }^2\sin \theta =0\end{array}}$

Utilizamos el procedimiento ode45 de MATLAB para integrar la ecuación duferencial de segundo orden con las siguientes condiciones iniciales τ=0, θ₀=π/6, dθ/dτ=0.

En la aproximación de oscilaciones de pequeña amplitud, el péndulo parte en el instante t=0 de la posición θ₀=π/6, con velocidad inicial dθ/dτ=0. Por lo que la amplitud es π/6 y la fase inicial π/2. La ecuación del Movimiento Armónico Simple es θ=(π/6)·sin(2πτ+π/2)

x0=zeros(1,2);
x0(1)=pi/6;
x0(2)=0;
f=@(t,x) [x(2);-4*pi^2*sin(x(1))]; 
tspan=[0 3];
[t,x]=ode45(f,tspan,x0);

xx=(pi/6)*sin(2*pi*t+pi/2); 

plot(t,x(:,1),'b',t,xx,'r')
grid on
xlabel('t/P_0')
ylabel('\theta');
title('Posición angular en función del tiempo')

Conservación de la energía

En la posición θ=θ₀ el péndulo solamente tiene energía potencial, que se transforma en energía cinética cuando el péndulo pasa por la posición de equilibrio.

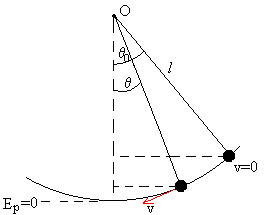
Comparemos dos posiciones del péndulo:

En la posición extrema θ=θ₀, la energía es solamente potencial.

E=mg(l-l·cosθ₀)

En la posición θ, la energía del péndulo es parte cinética y la otra parte potencial

${\displaystyle E=\frac{1}{2}m{v}^2+mg(l-l\cos \theta )}$

La energía se conserva

v²=2gl(cosθ-cosθ₀)

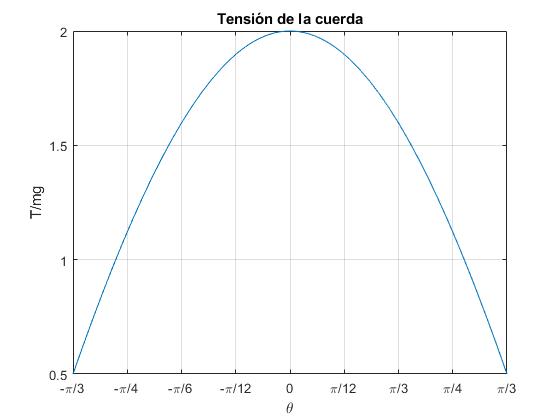
Tensión de la cuerda

La tensión de la cuerda en función del ángulo θ es

T=mg(3cosθ-2cosθ₀)

La tensión de la cuerda no es constante, sino que varía con la posición angular θ. Su valor máximo se alcanza cuando θ=0, el péndulo pasa por la posición de equilibrio (la velocidad es máxima). Su valor mínimo, cuando θ=θ₀ (la velocidad es nula).

th=pi/3;
fplot(@(x) 3*cos(x)-2*cos(th),[-pi/3,pi/3])
grid on
set(gca,'XTick',-pi/3:pi/12:pi/3)
set(gca,'XTickLabel',{'-\pi/3','-\pi/4','-\pi/6','-\pi/12','0',
'\pi/12','\pi/3','\pi/4','\pi/3'})
xlabel('\theta')
ylabel('T/mg')
title('Tensión de la cuerda')

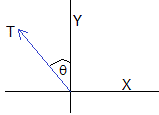
Las componentes rectangulares de la tensión de la cuerda son:

${\displaystyle \begin{array}{l}{F}_x=-T\sin \theta =-mg\left(3\cos \theta -2\cos {\theta }_0\right)\sin \theta \\ F_y=T\cos \theta =mg\left(3\cos \theta -2\cos {\theta }_0\right)\cos \theta \end{array}}$

Oscilaciones de pequeña amplitud

Cuando el ángulo θ es pequeño entonces, sinθ ≈ θ. La ecuación diferencial que describe las oscilaciones del péndulo se escribe

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{g}{l}\theta =0}$

La solución de esta ecuación diferencial es

θ=Asin(ωt)+Bcos(ωt), con frecuencia angular ω²=g/l

Los coeficientes A y B se determina a partir de las condiciones iniciales, la posición angular θ₀ y velocidad angular w₀=(dθ/dt)₀

${\displaystyle \begin{array}{l}\theta =A\cos (\omega t)+B\sin (\omega t)\\ \frac{d\theta }{dt}=\omega \left(-A\sin (\omega t)+B\cos (\omega t)\right)\\ t=\mathrm{0,}\{\begin{array}{l}{\theta }_0=A\\ {\left(\frac{d\theta }{dt}\right)}_0=\omega B\end{array}\\ \theta ={\theta }_0\cos (\omega t)+\frac{w_0}{\omega }\sin (\omega t)\end{array}}$

Habitualmente, el péngulo se separa θ₀ de la posición de equilibrio y se suelta, la velocidad angular inicial es w₀=0. La ecuación del movimiento es

θ=θ₀cos(ωt)

El periodo, P₀=2π/ω, del péndulo es

${\displaystyle P_0=2\pi \sqrt{\frac{l}{g}}}$

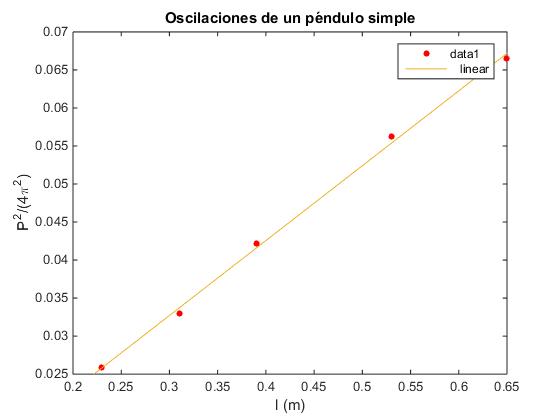
Experiencia de laboratorio

En una experiencia se han medido los periodos P de péndulos simples de longitud l. A partir de estos datos, se le pide calcular la aceleración de la gravedad g

En un sistema de ejes, se representa:

• P²/(4π²) en el eje vertical,
• la longitud l en m el eje horizontal,

se calcula y traza la recta que mejor ajusta a los datos y cuya pendiente es la inversa de la la aceleración de la gravedad g.

${\displaystyle \frac{P_0^2}{4{\pi }^2}=\left(\frac{1}{g}\right)l}$

>> x=[23 31 39 53 65]/100;
>> y=[1.01 1.14 1.29 1.49 1.62].^2/(4*pi^2);
>> plot(x,y,'ro','markersize',4,'markerfacecolor','r')
>> xlabel('l (m)')
>> ylabel('P^2/(4\pi^2)')
>> title('Oscilaciones de un péndulo simple')

En la ventana gráfica de MATLAB elegimos Tools/Basic fitting, activamos la casilla linear y obtenemos para la pendiente de la recta que mejor ajusta a los datos experimentales p1=0.098468. Por tanto, la aceleración de la gravedad es g=1/p1=10.1 m/s²