Equilibrio y estabilidad en un sistema electromecánico (I)

Sea un sistema formado por dos cargas Q y q. La carga Q está fija y la carga q está unida al extremo de un muelle de constante k, tal como se muestra en la figura.

Tomamos como origen la posición de la carga Q fija

Cuando no hay cargas la posición del extremo del muelle sin deformar respecto del origen O es x₀.
Cuando las cargas son del mismo signo, se repelen y la carga q se aleja de la carga fija Q. x>x₀.

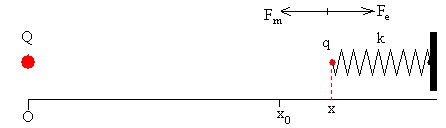
Cuando las cargas son del distinto signo, se atraen y la carga q se acerca a la carga fija Q. x<x₀.

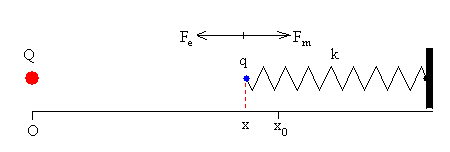
Este sistema en apariencia tan sencillo, presenta, sin embargo, un comportamiento complejo. Dada la carga q, determinaremos su posición de equilibrio estable si es que existiese.

Posiciones de equilibrio

La posición de equilibrio de la carga q es aquella en la que la fuerza de atracción o repulsión entre las cargas se compensa con la fuerza que ejerce el muelle.

En las dos figuras anteriores, se muestra el sentido de la fuerza de interacción entre cargas F_e y de la fuerza que ejerce el muelle F_m cuando las cargas son del mismo signo, y cuando son de sentido contrario. Para un valor dado de la carga q, la posición de equilibrio x se determina a partir de la igualdad

F_e=F_m

$\frac{1}{4 π ε_{0}} \frac{q \cdot Q}{x^{2}} = k (x - x_{0})$

x₀ es la longitud del muelle sin deformar y x es la longitud del muelle deformado.

$q = \frac{4 π ε_{0} k}{Q} x^{2} (x - x_{0})$

Elegimos la carga Q y la constante k del muelle de modo que $\frac{4 π ε_{0} k}{Q} = 1$ . O bien, elegimos un sistema de unidades en el que q se mide en unidades de $\frac{4 π ε_{0} k}{Q}$ .

q=x²(x-x₀)

Dada la carga q, resolvemos la ecuación cúbica para determinar la posición de equilibrio x.

Raíces de la ecuación cúbica

En la figura, se ha representado la función

y=x²(x-x₀)

dando valores a x en el intervalo entre (0.0, 1.1) y tomando x₀=1.0

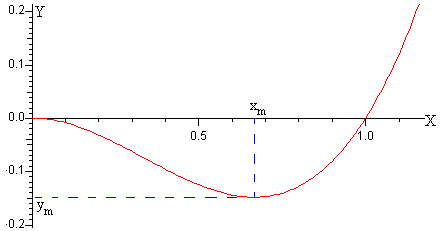
Como vemos la función presenta un mínimo que se calcula derivando y con respecto de x e igualando a cero.

$\frac{d y}{d x} = 3 x^{2} - 2 x x_{0} = 0 x_{m} = \frac{2}{3} x_{0} y_{m} = - \frac{4}{27} x_{0}^{3}$

Tomando con x₀=1.0, dado el valor de la carga q, se pueden presentar los siguientes casos:

No hay raíces reales

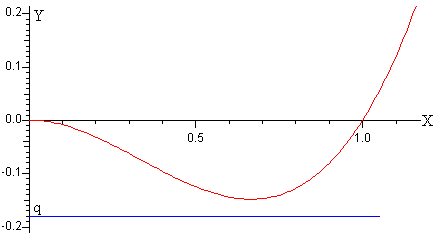
Cuando la carga q es inferior a q_m=y_m, tal como vemos en la figura, la solución de la ecuación cúbica no presenta raíces reales.

Cuando q<q_m la fuerza de atracción eléctrica domina a la fuerza que ejerce el muelle sobre la carga q

$\frac{F_{e}}{F_{m}} = \frac{Q}{4 π ε_{0} k} \frac{q}{x^{2} (x - x_{0})}$

Para cualquier valor de x<1, q es más grande en valor absoluto que el valor absoluto de y=x²(x-x₀). Las cargas Q y q se atraen hasta que coinciden en x=0.

Dos raíces reales

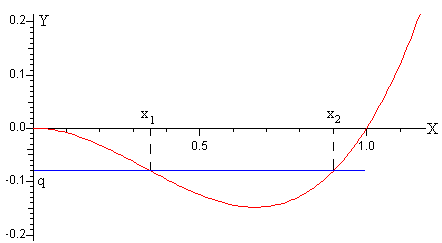
Cuando el valor de q está entre (q_m, 0) la recta y=q corta en dos puntos a la representación de la función cúbica.

Una sola raíz

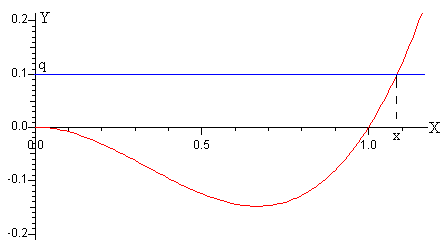
Cuando q>0 la recta y=q corta en un solo punto la representación gráfica

Estabilidad de las soluciones

La energía potencial del sistema es la suma de la energía potencial correspondiente a la interacción de las dos cargas eléctricas, y a la energía potencial almacenada en el muelle elástico cuando está deformado.

$E_{p} (x) = \frac{1}{4 π ε_{0}} \frac{Q \cdot q}{x} + \frac{1}{2} k {(x - x_{0})}^{2}$

Hemos elegido la carga Q y la constante k del muelle de modo que $\frac{4 π ε_{0} k}{Q} = 1$ .

$e_{p} (x) = \frac{q}{x} + \frac{1}{2} {(x - x_{0})}^{2}$

Las posiciones de equilibrio se calculan igualando a cero la derivada primera

$\frac{d e_{p} (x)}{d x} = \frac{- q}{x^{2}} + (x - x_{0}) = 0 x^{3} - x_{0} x^{2} - q = 0$

que es la ecuación que hemos estudiado en el apartado anterior

El signo de la derivada segunda de la energía potencial e_p(x) determina si la posición de equilibrio es estable (si es mayor que cero) o inestable (si es menor que cero).

$\frac{d^{2} e_{p} (x)}{d x^{2}} = \frac{2 q}{x^{3}} + 1$

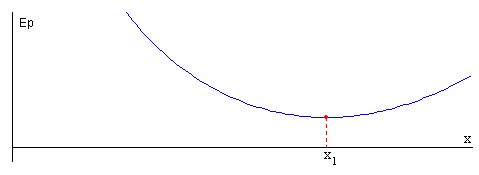
Cuando 0>q>q_m hay dos posiciones de equilibrio, a la posición x₁ corresponde un máximo de la energía potencial, y a la posición x₂ corresponde un mínimo. Por lo que x₂ es la posición de equilibrio estable.

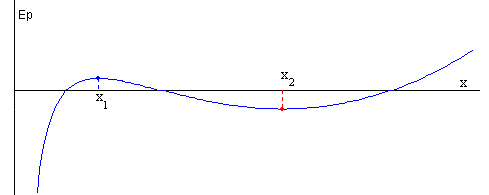
Cuando q disminuye el máximo y el mínimo se van acercando uno al otro hasta que coinciden en el valor de $x_{m} = \frac{2 x_{0}}{3}$ cuando $q = q_{m} = \frac{- 4 x_{0}^{3}}{27}$ , a dicho punto se le denomina de inflexión. Para esta posición, la derivada segunda de la energía potencial es cero.

La posición x_m que corresponde a q_m se denomina equilibrio neutro.

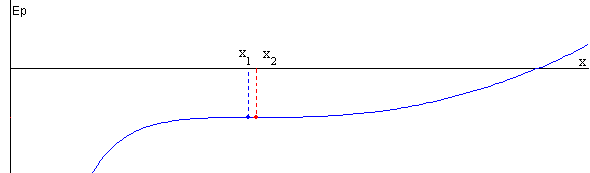
Cuando q>0, solamente hay una posición de equilibrio, que es estable, ya que corresponde a un mínimo de la energía potencial.

Actividades

Se introduce

La carga q, actuando en la barra de desplazamiento titulada Carga

Se pulsa el botón titulado Calcular

Se representa la curva de energía potencial e_p(x) y se señalan su máximo y su mínimo si los hubiere. La carga q unida al muelle se sitúa en la posición de equilibrio estable, siempre que q>q_m, y en el origen si q<q_m.

Se sugiere al lector, que calcule las raíces de la ecuación cúbica x³-x²-q=0 de forma gráfica, empleando papel milimetrado para distintos valores de q, tal como se ha explicado en esta página. También se puede usar la calculadora para hallar las raíces de la ecuación cúbica mediante las fórmulas del apartado "Raíces de una ecuación cúbica"

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Partensky M, Partensky P.D. Can a spring beat the charge?. The Physics Teacher, 42 November 2004, pp. 472-47