Equilibrio y estabilidad de un sistema electromecánico (II)
 En esta página, estudiamos la estabilidad de un sistema
electromecánico formado por un condensador plano-paralelo y un muelle elástico.
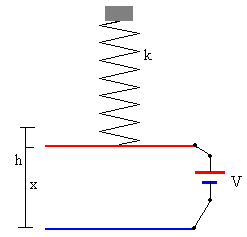
Como vemos en la figura, la placa inferior de un condensador plano-paralelo está
fija, la placa superior está unida a un muelle elástico de constante k.
Ambas placas están conectadas a una fuente cuya diferencia de potencial V puede cambiarse.
En esta página, estudiamos la estabilidad de un sistema
electromecánico formado por un condensador plano-paralelo y un muelle elástico.
Como vemos en la figura, la placa inferior de un condensador plano-paralelo está
fija, la placa superior está unida a un muelle elástico de constante k.
Ambas placas están conectadas a una fuente cuya diferencia de potencial V puede cambiarse.
Dada la diferencia de potencial V determinaremos la posición de equilibrio estable si es que existe.
Fuerzas sobre la placa
La posición de equilibrio es aquella en la que la fuerza de atracción entre las placas se compensa con la fuerza que ejerce el muelle.
Sea h la distancia entre las placas cuando el condensador no está conectado a la batería. Cuando se conecta la batería, las placas del condensador adquieren cargas iguales y opuestas y se atraen. Como consecuencia la separación entre las placas disminuye a x.
La fuerza que ejerce el muelle sobre la placa superior es k(h-x).
Fuerza de atracción entre las placas de un condensador conectado a una batería
Vamos a determinar la fuerza F de atracción entre las
placas, suponiendo que el condensador tiene una capacidad C y las placas
están cargadas con una carga q tal que q=C·V.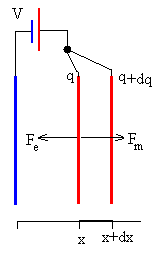
Supongamos que incrementamos en dx el espaciado entre las placas ejerciendo una fuerza mecánica exterior Fm sobre la placa móvil igual y opuesta a la fuerza de atracción eléctrica Fe entre las placas.
El trabajo realizado por esta fuerza es dWm=Fm·dx
Si las placas del condensador se mantienen a una diferencia de potencial constante V mediante una batería, al modificarse la capacidad, la batería realiza un trabajo para suministrar o retirar una carga dq=V·dC.
Este trabajo vale
dWV=V·dq=V2·dC
El trabajo total realizado sobre el condensador modifica la energía U=CV2/2 almacenada en el condensador en forma de campo eléctrico.
dU= dWV+ dWm
Como V es constante, tenemos que
Despejamos la fuerza Fm
Para un condensador plano-paralelo ideal C=ε0·S/x
La fuerza de atracción entre las placas Fe=-Fm es inversamente proporcional al cuadrado de su separación x.
Posiciones de equilibrio
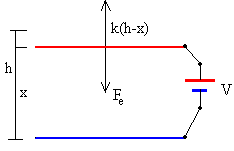
Igualando la fuerza que ejerce el muelle sobre la placa superior a la fuerza de atracción entre las placas
Obtenemos una ecuación cúbica en x.
Energía del sistema
Calculamos la energía del sistema formado por el condensador, la batería y el muelle elásticos
- La energía de un muelle de constante k deformado (h-x) es
- La energía almacenada en el condensador en forma de campo eléctrico es
- La batería suministra una energía
que es el doble de la energía acumulada en el condensador
La energía total del sistema es
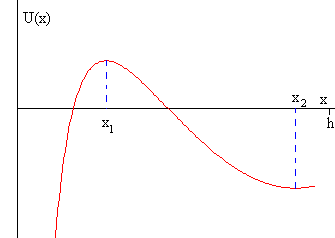
Las posiciones de equilibrio son aquellas en las que U(x) es máximo o mínimo
Obtenemos la ecuación cúbica en x.
Las posiciones de equilibrio estable son aquellas en las que U(x) es mínimo
Una de las raíces de la ecuación cúbica es negativa. Las otras dos x1 y x2 corresponden a un máximo y a un mínimo, respectivamente.
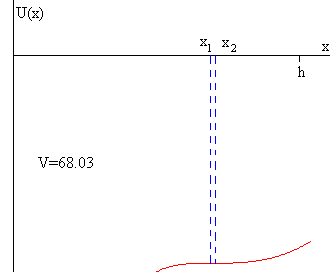
A medida que aumentamos la diferencia de potencial V, las posiciones de equilibrio estable e inestable se van acercando. Se hacen iguales en el punto de inflexión, cuando la derivada segunda de U respecto de x se anula.
Sustituyendo la raíz doble x en la ecuación cúbica
A medida que la diferencia de potencial V entre las palcas aumenta la separación disminuye hasta el límite 2h/3. Si se aumenta la diferencia de potencial de las placas por encima del valor límite, se juntan y su separación es nula.
Simulación
En la simulación la separación x entre las placas del condensador es en mm=10-3 m
Posiciones de equilibrio
Una raíz es negativa, otra raíz, x1 corresponde a la separación de equilibrio inestable y la tercera, x2 a la separación de equilibrio estable.
Las dos raíces se hacen iguales en el punto de inflexión
Sustituyendo la raíz doble x en la ecuación cúbica
La mínima separación entre placas es 2h/3 y la diferencia de potencial límite Vl es
Si se incrementa la diferencia de potencial V por encima del valor límite, las placas se juntan.
Actividades
Se introduce
- La diferencia de potencial V entre las placas del condensador, actuando en la barra de desplazamiento titulada d. d. Potencial.
- La separación entre las placas del condensador cuando no está conectado a la batería se ha fijado en h=25 mm
- El valor de la constante, K=1
Se pulsa el botón titulado Conectar
En la parte izquierda del applet, se representa el condensador, cuyas placas están unidas a una fuente de potencial ajustable. La placa superior del condensador está unida a un muelle elástico.
En la parte derecha, se representa la energía U del sistema formado por la batería, el condensador y el muelle elástico, en función de la separación x entre placas. Se señala la posición de equilibrio inestable x1 y la de equilibrio estable x2 mientras la diferencia de potencial V sea inferior al valor límite Vl.
Observamos que la carga q de las placas del condensador no es constante, cambia al cambiar la diferencia de potencial V y la capacidad del condensador. La intensidad del color azul (placa negativa) o rojo (placa positiva) señalan una mayor o menor carga en las placas.
Referencias
Physics challenge for Teachers and students. A touchy subject. Solution to February 2008 challenge. The Physics Teacher Vol. 46, 2008
