• Inicio
• Dinámica
• Trabajo y energía
• Equilibrio y estabilidad

Equilibrio y estabilidad en un sistema electromecánico (III)

Dos partículas idénticas cargadas de masa m con cargas q iguales y opuestas se cuelgan de dos hilos inextensibles de longitud d separados inicialmente x₀, tal como se muestra en la figura.

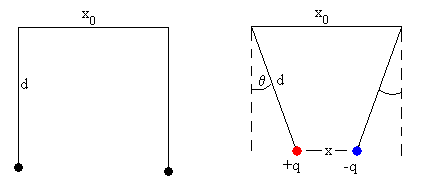
Normalmente, la separación de las cargas x es una función continua de la carga de las partículas, q. Al aumentar la carga la separación disminuye. Sin embargo, para cierto valor de la carga q_c de las partículas el sistema experimenta una transición discontinua a un nuevo estado de equilibrio en el que la separación x=0.

Equilibrio

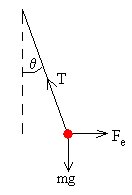Las cargas de distinto signo se atraen, acercándose a una distancia x. Los hilos forman un ángulo θ con la vertical.

Las fuerzas sobre cada una de las partículas son:

• La fuerza que ejerce el hilo, es decir, la tensión del hilo, T

• La fuerza de atracción eléctrica, $F_e=\frac{1}{4\pi {\epsilon }_0}\frac{q·q}{x^2}$

• El peso, mg

 

En el equilibrio

${\displaystyle T\sin \theta =\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{x^2}T\cos \theta =mg}$

Dividiendo las dos ecuaciones eliminamos la tensión T del hilo

${\displaystyle \tan \theta =\frac{1}{4\pi {\epsilon }_{0}mg}\frac{q^2}{x^2}}$

El ángulo θ está relacionado con la separación x entre las partículas, véase la primera figura

${\displaystyle \sin \theta =\frac{x_0-x}{2d}}$

Calculamos la separación de equilibrio x, hallando la raíz de la ecuación

${\displaystyle \frac{x_0-x}{\sqrt{4d^2-{(x_0-x)}^2}}=\frac{1}{4\pi {\epsilon }_{0}mg}\frac{q^2}{x^2}}$

Estabilidad

Energía potencial del sistema formado por las dos cargas es la suma de la energía potencial gravitatoria, las cargas se elevan d-d·cosθ, y la energía potencial electrostática, que es negativa por ser la fuerza atractiva.

${\displaystyle \begin{array}{l}{E}_p=2mg(d-d\cos \theta )-\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{x}\\ E_p=4mgd{\sin }^2\left(\frac{\theta }{2}\right)-\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{x}\end{array}}$

La posición de equilibrio es estable si la energía potencial es mínima en dicha posición, y es inestable si la energía potencial es máxima.

El signo de la derivada segunda de la energía potencial E_p(x) determina si la posición de equilibrio es estable (si es mayor que cero)  o inestable (si es menor que cero).

Aproximaciones

Cuando d>>x₀, el ángulo θ es muy pequeño y podemos realizar las siguientes aproximaciones que simplifican notablemente los cálculos, tanθ≈sinθ≈θ

La ecuación que calcula la separación de equilibrio x se convierte en

${\displaystyle \frac{x_0-x}{2d}\approx \frac{1}{4\pi {\epsilon }_{0}mg}\frac{q^2}{x^2}}$

Tenemos que calcular las raíces de una ecuación cúbica

${\displaystyle x^3-x_0{x}^2+\frac{d{q}^2}{2\pi {\epsilon }_{0}mg}=0}$

La energía potencial se aproxima a

${\displaystyle E_p(x)=mg\frac{{(x_0-x)}^2}{4d}-\frac{1}{4\pi {\epsilon }_0}\frac{q^2}{x}}$

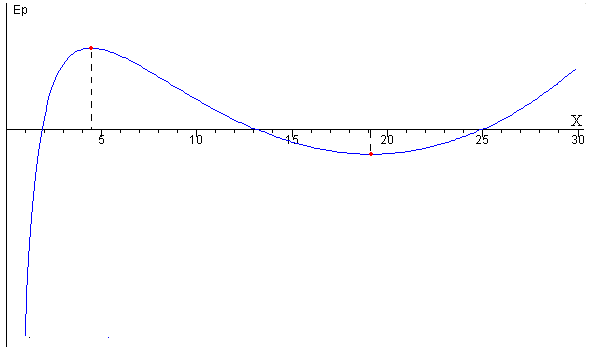
A medida que se aumenta la carga q de las partículas, el máximo y el mínimo se acercan, para un cierto valor de la carga q_c coinciden en el punto de inflexión

${\displaystyle \frac{d^2{E}_p(x)}{d{x}^2}=\frac{mg}{2d}-\frac{1}{2\pi {\epsilon }_0}\frac{q_c^2}{x^3}=0}$

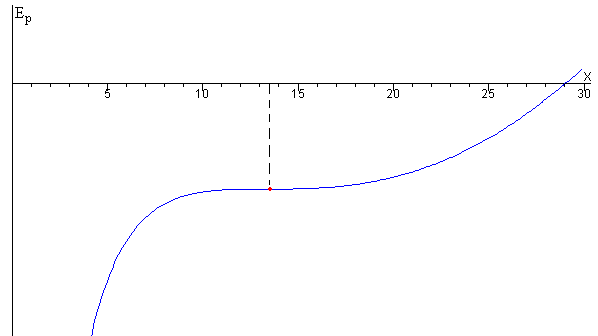
Despejamos x y lo introducimos en la ecuación cúbica que nos proporciona las posiciones de equilibrio

${\displaystyle \begin{array}{l}{x}^3=\frac{q_c^{2}d}{\pi {\epsilon }_{0}mg}\\ \frac{q_c^{2}d}{\pi {\epsilon }_{0}mg}-x_0{\left(\frac{q_c^{2}d}{\pi {\epsilon }_{0}mg}\right)}^{2/3}+\frac{q_c^{2}d}{2\pi {\epsilon }_{0}mg}=0\\ q_c=\frac{2x_0}{3}\sqrt{\frac{2\pi x_0{\epsilon }_{0}mg}{3d}}\end{array}}$

Si la carga de las partículas q>q_c las dos partículas se juntan x=0.

Ejemplo:

• Masa de las partículas m=0.001 kg

• Carga de las partículas q=13·10^-9 C

• Longitud del hilo d=1.0 m

• Separación entre las partículas no cargadas x₀=0.2 m

Las raíces de la ecuación cúbica

${\displaystyle x^3-x_0{x}^2+\frac{d{q}^2}{2\pi {\epsilon }_{0}mg}=0}$

x³-0.2x²+3.276·10^-4 =0

cuyas raíces son

x₁=-0.0362, x₂=0.195, x₃=0.0447 m

La primera no es físicamente posible, la segunda corresponde a un mínimo de la energía potencial (posición de equilibrio estable) y la tercera, corresponde a un máximo (posición de equilibrio inestable).

La carga crítica q_c y la separación de equilibrio de las cargas es

${\displaystyle \begin{array}{l}{q}_c=\frac{2x_0}{3}\sqrt{\frac{2\pi x_0{\epsilon }_{0}mg}{3d}}=25.4·{10}^{-9}\text{C}\\ x=\sqrt[3]{\frac{q_c^{2}d}{\pi {\epsilon }_{0}mg}}=13.3\text{cm}\end{array}}$

Si la carga de las partículas q>q_c las dos partículas se juntan, su separación x=0.

En realidad, las partículas tienen un tamaño y no pueden ocupar la misma posición.

Actividades

Se ha fijado

• La masa de las partículas, m=0.001 kg

• La longitud del hilo, d=1.0 m

• La separación entre las partículas no cargadas x₀=0.2 m

Se introduce

• La carga q de las partículas en unidades 10^-9 C, actuando en la barra de desplazamiento titulada Carga.

Se pulsa el botón titulado Calcular

Se representa a las dos partículas en la posición de equilibrio estable.

En la parte derecha del applet, se representa la energía potencial en E_p en función de la separación x entre las partículas. Se señala el máximo y el mínimo, si existen.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Curso Interactivo de Física en Internet © Ángel Franco García