• Inicio
• Dinámica
• Sistemas de partículas

Una cuerpo desliza sobre un plano inclinado móvil

En esta página, se estudia el movimiento de un cuerpo que desliza a lo largo de un plano inclinado que a su vez, se mueve sin fricción sobre una superficie horizontal. Este es un problema clásico en un curso de Física General.

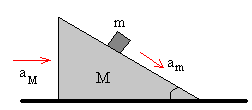El plano inclinado es una cuña de masa M, que forma un ángulo θ con la horizontal. Un cuerpo de masa m desliza sobre el plano inclinado. El coeficiente de rozamiento entre las dos superficies en contacto es μ.

• La aceleración del bloque respecto de la cuña es a_m, su dirección es paralela al plano inclinado

• La aceleración de la cuña respecto de Tierra es a_M, en la dirección horizontal

Suponemos inicialmente que a_M tiene el sentido hacia la derecha (positivo). Como veremos, la conservación del momento lineal o las ecuaciones del movimiento nos darán el sentido correcto, hacia la izquierda (negativo).

Descripción

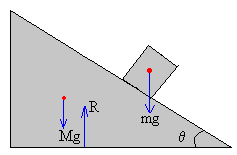
En la figura, se muestra las fuerzas sobre cada uno de los dos cuerpos y las aceleraciones de los mismos

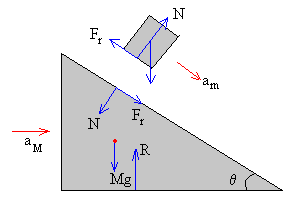
Sobre el bloque actúan

• El peso mg

• La reacción N del plano inclinado

• La fuerza de rozamiento, F_r que se opone a su movimiento hacia abajo a lo largo del plano inclinado

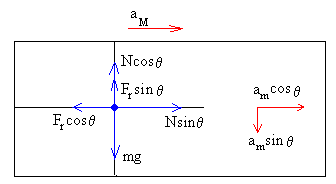
Las ecuaciones del movimiento del bloque son

1. A lo largo del eje horizontal, la aceleración del bloque respecto de Tierra es (a_m·cosθ+a_M)

N·sinθ-F_r·cosθ=m(a_m·cosθ+a_M)       (1)

2. A lo largo del eje vertical, la aceleración del bloque respecto de Tierra es a_m·senθ

mg-N·cosθ-F_r·sinθ= m·a_m·sinθ           (2)

3. Si μ es el coeficiente de la fuerza de rozamiento

F_r=μ·N

Sobre la cuña actúan

• El peso Mg en su centro de masas

• Por la tercera ley de Newton, las fuerzas que ejerce la cuña sobre el bloque son iguales y de sentido contrario a las que ejerce el bloque sobre la cuña.

• La reacción R del plano horizontal a lo largo del cual desliza la cuña sin rozamiento.

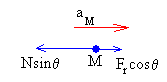
A lo largo del eje horizontal, la ecuación del movimiento es

F_r·cosθ-N·sinθ=M·a_M       (3)

A lo largo de la dirección vertical, la cuña está en equilibrio.

Sumando la primera y tercera ecuación, obtenemos la relación entre las aceleraciones a_m y a_M.

m(a_m·cosθ+a_M)+ M·a_M=0

${\displaystyle a_M=-\frac{m{a}_m\cos \theta }{m+M}}$

La aceleración de la cuña a_M es de sentido contrario al señalado en las figuras.

Despejamos del sistema de ecuaciones la aceleración a_m del bloque respecto de la cuña y la aceleración de la cuña a_M respecto de Tierra.

${\displaystyle a_m=\frac{(m+M)g(\tan \theta -\mu )·\cos \theta }{m+M-m(1+\mu \tan \theta ){\cos }^2\theta }{a}_M=-\frac{mg(\tan \theta -\mu )·{\cos }^2\theta }{m+M-m(1+\mu \tan \theta ){\cos }^2\theta }}$

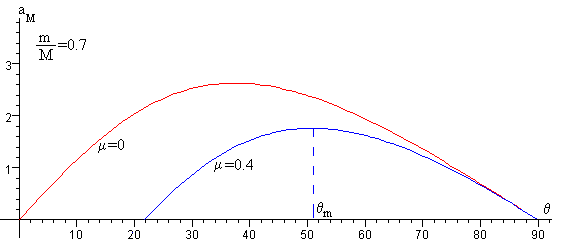
En la figura, se representa de a_M en función del ángulo θ para dos valores del coeficiente de rozamiento μ=0, (cuando no hay rozamiento) y μ=0.4. Vemos que a_M presenta un máximo para un ángulo θ_m. Cuando μ≠0, a_M es positivo a partir de cierto ángulo θ₀. Este ángulo es precisamente aquél tanθ₀= μ.

Por ejemplo, cuando μ=0.4, θ₀=22º. Evidentemente, cuando no hay rozamiento μ=0, θ₀=0º.

En el estudio del movimiento de un cuerpo a lo largo de un plano inclinado de ángulo θ, ya se puso de manifiesto que el cuerpo desliza con velocidad uniforme justamente cuando tanθ=μ. Para ángulos mayores, el cuerpo desliza con movimiento acelerado.

De las ecuaciones del movimiento rectilíneo uniformemente acelerado, obtenemos la velocidad y el desplazamiento de los cuerpos:

• La velocidad del bloque respecto de la cuña es v_m=a_m·t, suponiendo que parte del reposo.

• El desplazamiento del bloque sobre la cuña es $x_m=\frac{1}{2}{a}_m{t}^2$

• La velocidad de la cuña respecto de tierra es v_M=a_M·t

• El desplazamiento de la cuña a lo largo del plano horizontal es $x_M=\frac{1}{2}{a}_M{t}^2$

El bloque llega al vértice de la cuña en el instante

${\displaystyle t_m=\sqrt{\frac{2l}{a_m}}}$

donde l es el desplazamiento total del bloque a lo largo de la cuña.

• La cuña se mueve en el plano horizontal a partir de este instante con velocidad constante

v_M=a_M·t_m

• El bloque se mueve en el plano horizontal con velocidad constante respecto de Tierra,

V_m=v_M+a_m·t_m·cosθ

Sistema de partículas

Podemos considerar al bloque y la cuña como un sistema de dos partículas interactuantes

Las fuerzas interiores o de interacción mutua son

• La reacción N

• La fuerza de rozamiento entre ambas superficies F_r.

Las fuerzas interiores que actúan sobre cada cuerpo son iguales y de sentido contrario.

Las fuerzas exteriores como se muestra en la figura, son:

• Los pesos mg y Mg, que actúan sobre el centro de masas de cada uno de los cuerpos

• La fuerza R que ejerce el plano horizontal sobre la cuña.

El sistema está verticalmente en equilibrio de modo que R=mg+Mg. La posición de dicha fuerza, depende de la posición del bloque sobre la cuña, y de las masas del bloque M y de la cuña m.

A lo largo del eje horizontal, no hay fuerza exterior.

• La componente horizontal de la aceleración del centro de masas es cero, la velocidad horizontal del centro de masas es constante.

• Si en el instante inicial el centro de masas estaba en reposo, la componente X_c no cambiará a lo largo del movimiento del bloque y la cuña.

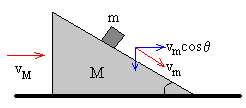
• Como el momento lineal inicial es cero, la componente del momento lineal a lo largo del eje horizontal p_x también será cero.

M·v_M+m(v_M+v_m·cosθ)=0

Derivando con respecto del tiempo, obtenemos la relación entre las aceleraciones a_m y a_M.

Actividades

Se introduce

• El ángulo θ, del plano inclinado, actuando en la barra de desplazamiento titulada Angulo.

• El coeficiente de rozamiento μ, entre el bloque y el plano inclinado, en el control de edición titulado Coef. rozamiento

• El cociente entre las masas del bloque y de la cuña, m/M, en el control de edición titulado Masa bloque/cuña

Se pulsa el botón titulado Nuevo

Si los datos introducidos son correctos, es decir, si se cumple que tanθ>μ se pulsa el botón titulado Empieza. En caso contrario, un mensaje nos avisa de que hemos de disminuir el coeficiente de rozamiento o aumentar el ángulo del plano inclinado.

Se observa, el movimiento de la cuña y el movimiento del bloque a lo largo del plano inclinado. La posición del c.m. del bloque y de la cuña, y la posición del c.m. del sistema formado por ambos cuerpos. Comprobamos que el c.m. del sistema se encuentra en reposo horizontalmente, la coordenada X_c no cambia.

En la parte superior del applet, se nos proporciona los datos del tiempo, aceleración, velocidad y posición del bloque respecto de la cuña, y de la cuña respecto de Tierra. Cuando el bloque termina su movimiento sobre la cuña y desliza sobre el plano horizontal sin rozamiento, las posiciones y velocidades se refieren a Tierra.

Como el objetivo del programa interactivo es la medida de la posición, velocidad y aceleración de la cuña. Se ha invertido el sentido del movimiento respecto de la explicación dada en el texto. La aceleración, velocidad y posición de la cuña son positivos y los del bloque son negativos.

Ejemplo:

Sea

• Cociente entre la masa del bloque y de la cuña, m/M=0.7

• Coeficiente de rozamiento, μ=0.4

• Ángulo del plano inclinado, θ=30º

Calculamos la aceleración del bloque a_m con respecto a la cuña.

${\displaystyle a_m=\frac{(0.7+1)·9.8·(\tan 30º-0.4)·\cos 30º}{0.7+1-0.7(1+0.4\tan 30º){\cos }^{2}30º}=2.43{\text{m/s}}^{\text{2}}}$

Calculamos la aceleración de la cuña a_M respecto de Tierra

${\displaystyle a_M=-\frac{m{a}_m\cos \theta }{m+M}{a}_M=-\frac{0.7·2.43·\cos 30}{0.7+1}=-0.87{\text{m/s}}^{\text{2}}}$

El tiempo que tarda el bloque en recorrer el plano inclinado de longitud l=1 m es

${\displaystyle t_m=\sqrt{\frac{2l}{a_m}}{t}_m=\sqrt{\frac{2·1.0}{2.43}}=\text{0}\text{.91}\text{s}}$

La velocidad de la cuña en este instante es

v_M=a_M·t_m=-0.79 m/s

La velocidad del bloque respecto de la cuña en dicho instante es

v_m=a_m·t_m=2.20 m/s

La velocidad del bloque respecto de Tierra a partir de dicho instante es

V_m=v_m·cosθ+v_M=1.12 m/s

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Bolina O, Rodrigo Parreira. A problem of relative, costrained motion. The Physics Teacher, Vol 36, September 1998, pp. 334-335

Curso Interactivo de Física en Internet © Ángel Franco García