Movimiento de caída bajo la fuerza de atracción mutua.

Vamos a estudiar en esta sección el movimiento de caída de dos cuerpos de masas m₁ y m₂ bajo la fuerza de atracción mutua.

Supongamos que inicialmente los dos cuerpos están en reposo, separados una distancia r entre ambos. El centro de masa estará en reposo a una distancia r₁ del cuerpo de masa m₁ y a una distancia r₂ del cuerpo de masa m₂, como vemos en la figura.

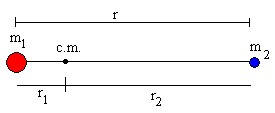m₁r₁=m₂r₂

r=r₁+r₂

$r_{1} = \frac{m_{2} r}{m_{1} + m_{2}} r_{2} = \frac{m_{1} r}{m_{1} + m_{2}}$

Como el sistema de dos partículas es aislado el centro de masas continuará en reposo en la misma posición.

Si establecemos el origen en el c.m. las ecuaciones del movimiento de los dos cuerpos son

$\begin{array}{l} m_{1} \frac{d^{2} r_{1}}{d t^{2}} = - G \frac{m_{1} m_{2}}{r^{2}} \\ m_{2} \frac{d^{2} r_{2}}{d t^{2}} = - G \frac{m_{1} m_{2}}{r^{2}} \end{array}$

Escribiendo r₁ o r₂ en función de r,

$\begin{array}{l} \frac{m_{1} \cdot m_{2}}{m_{1} + m_{2}} \frac{d^{2} r}{d t^{2}} = - G \frac{m_{1} \cdot m_{2}}{r^{2}} \\ μ \frac{d^{2} r}{d t^{2}} = - G \frac{m_{1} \cdot m_{2}}{r^{2}} \end{array}$

El movimiento de las dos cuerpos es equivalente al movimiento de una partícula de masa reducida m , bajo la acción de la fuerza que describe la interacción mutua, la fuerza de atracción entre las dos masas separadas una distancia r=r₁+r₂

Eliminando el producto m₁·m₂

$\frac{d^{2} r}{d t^{2}} = - G \frac{m_{1} + m_{2}}{r^{2}}$

Supongamos que la separación inicial entre los dos cuerpos es r₀. Definimos las variables adimensionales

x=r/r₀,
τ=t/P

Siendo P el periodo del movimiento circular cuando ambos cuerpos están separados una distancia r₀.

$P^{2} = \frac{4 π^{2} r_{0}^{3}}{G (m_{1} + m_{2})}$

La ecuación del movimiento se transforma en otra más simple.

$\frac{r_{0}}{P^{2}} \frac{d^{2} x}{d τ^{2}} = - \frac{G (m_{1} + m_{2})}{r_{0}^{2} \cdot x^{2}} \frac{d^{2} x}{d τ^{2}} = - \frac{4 π^{2}}{x^{2}}$

Integramos esta ecuación diferencial con las condiciones iniciales τ=0, x=1, v=dx/dτ=0.

Empleando la regla de la cadena transformamos una ecuación diferencial de segundo orden en una de primer orden.

$\frac{d^{2} x}{d τ^{2}} = \frac{d v}{d τ} = \frac{d v}{d x} \frac{d x}{d τ} = v \frac{d v}{d x} = - \frac{4 π^{2}}{x^{2}}$

Obtenemos la velocidad v relativa de un cuerpo respecto del otro integrando la ecuación diferencial de primer orden con la condición inicial x=1, v=0

$\int_{0}^{v} v \cdot d v = - 4 π^{2} \int_{1}^{x} \frac{d x}{x^{2}} \frac{v^{2}}{2} = 4 π^{2} (\frac{1}{x} - 1)$

Cuando los cuerpos caen, x disminuye con τ, la velocidad v es negativa. Tenemos que integrar la ecuación diferencial de primer orden

$\frac{d x}{d τ} = - 2 \sqrt{2} π \sqrt{\frac{1 - x}{x}}$

con las condiciones iniciales τ=0, x=1.

$\int_{1}^{x} \sqrt{\frac{x}{1 - x}} d x = - 2 \sqrt{2} π \int_{0}^{τ} d τ$

La integral del miembro izquierdo se resuelve haciendo la sustitución

$z^{2} = \frac{x}{1 - x} d x = \frac{2 z}{{(1 + z^{2})}^{2}} d z$

A continuación, se integra por partes quedando

$\frac{- z}{1 + z^{2}} + \arctan z$

Deshaciendo el cambio, evaluando el integrando para el límite superior e inferior, despejamos el tiempo adimensional τ.

$τ = \frac{1}{2 \sqrt{2} π} (\sqrt{x - x^{2}} - \arctan \sqrt{\frac{x}{1 - x}} + \frac{π}{2}) = \frac{1}{2 π \sqrt{2}} (\sqrt{x - x^{2}} + \arcsin \sqrt{1 - x})$ (1)

Tenemos una ecuación implícita τ=τ(x), dado el valor de x podemos calcular el tiempo τ.

Ejemplo 1:

Cuerpo	Masa (kg)	Radio (m)
Sol	1.98·10 ²⁰	6.96·10⁸
Tierra	5.98·10²⁴	6.37·10⁶
Luna	7.34·10²²	1.74·10⁶

Sea el sistema formado por la Tierra y el Sol. Supongamos que la Tierra se detiene cuando está a una distancia de una unidad astronómica r₀=1.49·10¹¹ m del centro del Sol.

La posición inicial del Sol y de la Tierra respecto del origen situado en el c.m. es

$r_{1} = \frac{5.98 \cdot 10^{24}}{5.98 \cdot 10^{24} + 1.98 \cdot 10^{30}} 1.49 \cdot 10^{11} = 4.5 \cdot 10^{5} m$

a la izquierda del c.m.

r₂=1.49·10¹¹-4.5·10⁵=1.49·10¹¹ m

a la derecha del c.m.

El centro de masas del sistema formado por la Tierra y el Sol está muy cerca del centro del Sol que permanecerá prácticamente inmóvil dada su gran diferencia de masa con respecto de la Tierra.

Supongamos que la Tierra cae hacia el Sol, entra en contacto con el Sol, cuando la separación entre sus centros es r=6.96·10⁸+6.37·10⁶ m.

La Tierra está en reposo cuando su distancia del centro del Sol es x=1, y entra en contacto con el Sol cuando su separación es x=r/r₀=0.0047.

Calculamos el valor del tiempo adimensional τ=0.177 mediante la fórmula (1).

Calculamos el periodo P de la órbita circular de la Tierra alrededor del Sol.

$P = 2 π \sqrt{\frac{{(1.49 \cdot 10^{11})}^{3}}{6.67 \cdot 10^{- 11} (1.98 \cdot 10^{30} + 5.98 \cdot 10^{24})}} = 31445832 s = 364 días$

El instante en el que entran en contacto el Sol y la Tierra es t= τ·P=5558126 s=64 días.

Los centros de ambos cuerpos celestes coinciden r=0, ó x=0 en el instante

$t = P \frac{1}{4 \sqrt{2}} = 5558890 s$

Ejemplo 2:

La distancia entre los centros de la Tierra y de la Luna es 3.84·10⁸ m

La posición de la Tierra y la Luna respecto del origen situado en el c.m. cuando su separación es r=x·3.84·10⁸ m es

$r_{1} = \frac{7.34 \cdot 10^{22}}{5.98 \cdot 10^{24} + 7.34 \cdot 10^{22}} 3.84 \cdot 10^{8} \cdot x$

a la izquierda del c.m.

r₂=3.84·10⁸-r₁m

a la derecha del c.m.

El periodo P de la órbita circular de la Luna y de la Tierra alrededor de su c.m. común es

$P = 2 π \sqrt{\frac{{(3.84 \cdot 10^{8})}^{3}}{6.67 \cdot 10^{- 11} (7.34 \cdot 10^{22} + 5.98 \cdot 10^{24})}} = 2352958 s = 27 días$

Si se detiene la Tierra y la Luna cuando su distancia es r₀=3.84·10⁸ m o x=1. Sus centros coinciden r=0, ó x=0, en el instante t

$t = P \frac{1}{4 \sqrt{2}} = 415948 s = 5 días$

Actividades

Se introduce

La masa m₁ del primer cuerpo, en el control de edición titulado Masa 1
La masa m₂ del primer cuerpo, en el control de edición titulado Masa 2
La distancia inicial r₀ entre ambos cuerpos, en el control de edición titulado Distancia
En vez de introducir directamente los datos, se puede seleccionar el par de cuerpos celestes, en el control de selección titulado Ejemplos.

Se pulsa el botón titulado Empieza

Nota: para introducir en un control de edición un número en notación exponencial, por ejemplo 1.49·10¹¹, se escribe 1.49e11.

Se observa el movimiento de los dos cuerpos, en su movimiento de caída, hasta que los centros de ambos coinciden r=0 ó x=0.

En la parte superior del applet se proporciona.

El tiempo adimensional τ, y la distancia adimensional x entre los cuerpos.
El tiempo t en segundos, y la posición r₁ y r₂ en metros de cada unos de los cuerpos respecto del origen situado en el centro de masa.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Stewart M. Falling and orbiting. The Physics Teacher, Vol 36, February 1998, pp. 122-125.