Efectos mecánicos de la ley de Faraday

Un ejemplo ilustrativo de la ley de Faraday es el de una espira cuadrada que atraviesa una región donde existe un campo magnético uniforme:

Cuando la espira se introduce en el campo magnético, se produce una fem que se opone al incremento del flujo del campo magnético a través de dicha espira.
Cuando la espira está introducida en dicha región, el flujo es constante y no se produce fem alguna
Cuando la espira sale de dicha región, el flujo a través de la espira disminuye y se produce una fem que se opone a la disminución de flujo.

También estudiamos las fuerzas sobre la espira, concluyendo que cuando la espira entra o cuando sale de dicha región, la fuerza que ejerce el campo magnético sobre la corriente inducida en la espira se opone al movimiento de la espira.

Hemos supuesto que sobre la espira se aplica una fuerza que hace que la espira atraviese dicha región con velocidad constante.

Por tanto, si una espira se introduce en un campo magnético con velocidad inicial v₀ y no se aplican fuerzas exteriores, la espira experimentará una fuerza de frenado, que disminuirá su velocidad hasta que toda la espira esté dentro de la región en la que existe campo magnético y de nuevo, se volverá a frenar cuando salga de dicha región.

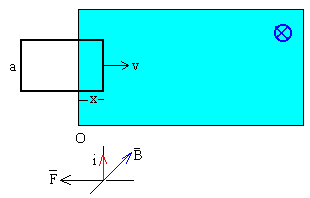
Vamos a estudiar el comportamiento de un espira rectangular de anchura a que se mueve con velocidad inicial v₀ para x<0 y que se introduce en un campo magnético uniforme que existe en la región x≥ 0. La espira será lo suficientemente larga para que solamente consideremos la situación en la que su lado derecho está introducido en la región en la que existe el campo magnético.

En esta página, se pretende subrayar el comportamiento completamente diferente de un elemento resistivo en comparación con otro inductivo. En primer lugar, consideramos que la espira tiene resistencia pero no autoinducción. En el segundo caso, se considera que la espira tiene autoinducción pero no resistencia. En una página adicional, se estudia el comportamiento de la espira cuando tiene a la vez resistencia y autoinducción, pero no se simula en un applet debido a su complejidad y a que no añade nada nuevo conceptualmente.

Autoinducción nula (R≠ 0, L=0)

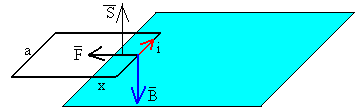Si la espira de anchura a, se ha introducido x en la región en la que existe campo magnético que apunta perpendicularmente al plano del dibujo y hacia dentro, el flujo a través de la espira será

Φ =B·S=-B·(ax)

Aplicando la ley de Faraday se obtiene la fem

$V_{ε} = \frac{d Φ}{d t} = B a v$

De acuerdo a la ley de Lenz el sentido de la corriente inducida i es antihorario, ya que el flujo aumenta.

Para una espira de resistencia R, la ecuación del circuito es Vε =iR

$i = \frac{B a v}{R}$

La fuerza sobre el lado derecho de la espira es

$F = i u_{t} \times B \cdot l F = - i B a = - \frac{B^{2} a^{2}}{R} v$

de sentido contrario a la velocidad v de la espira.

La ecuación del movimiento de la espira será

$m \frac{d v}{d t} = - \frac{B^{2} a^{2}}{R} v$

y la solución de la ecuación diferencial, con las condiciones iniciales t=0, v=v₀, es

$v = v_{0} \exp (- \frac{t}{τ}) τ = \frac{R m}{B^{2} a^{2}}$

La velocidad v de la espira disminuye exponencialmente con el tiempo.

A partir de la expresión de la velocidad en función del tiempo obtenemos la posición x del móvil que parte del origen en el instante inicial t=0, x=0

$x = \int_{0}^{t} v d t = \frac{v_{0}}{k} (1 - \exp (- t / τ))$

A partir de la ecuación del circuito obtenemos la intensidad en función del tiempo

$i = \frac{B a}{R} v_{0} \exp (- \frac{t}{τ})$

La intensidad i que circula por la espira disminuye exponencialmente con el tiempo.

Estas ecuaciones se aplican mientras que el lado derecho de la espira esté en el seno del campo magnético. Cuando ambos lados estén dentro de la región x≥ 0, la intensidad de la corriente inducida será cero y la fuerza que ejerce el campo magnético sobre la espira será nula y por tanto, la velocidad de la espira será constante.

Estudio energético

Podemos comprobar que la energía cinética inicial de la espira E_k, se disipa en la resistencia de la espira. La ley de Joule afirma que la energía por unidad de tiempo (potencia) disipada en la resistencia es i²R.

Comprobamos que en cualquier instante, la suma de la energía cinética E_k de la espira y de la energía disipada en la resistencia E_R es igual a la energía cinética inicial de la espira.

$\begin{array}{l} E_{k} = \frac{1}{2} m v^{2} = \frac{1}{2} m v_{0}^{2} \exp (- 2 t / τ) \\ E_{R} = \int_{0}^{t} i^{2} R \cdot d t = \frac{1}{2} m v_{0}^{2} (1 - \exp (- 2 t / τ)) \\ E_{k} + E_{R} = \frac{1}{2} m v_{0}^{2} \end{array}$

Resistencia nula (L≠ 0, R=0)

Consideremos que la espira está hecha de un material superconductor de modo que R≈0. En este caso, no podemos ignorar la autoinducción L, que produce una fem

$V_{L} = - L \frac{d i}{d t}$

La ecuación del circuito (suma de fems igual a intensidad por resistencia) se escribe ahora V_L+V_ε =0.

$- L \frac{d i}{d t} + B a \frac{d x}{d t} = 0 i = \frac{B a}{L} x$

que satisface la condición inicial x=0, i=0.

La fuerza que ejerce el campo magnético sobre el lado derecho de la espira será de nuevo F=-iaB, por lo que la ecuación del movimiento se escribirá

$m \frac{d^{2} x}{d t^{2}} + \frac{B^{2} a^{2}}{L} x = 0$

Esta es la ecuación diferencial de un oscilador libre, que describe el Movimiento Armónico Simple x=A·sin(ω₀ t+φ ).

A partir de las condiciones iniciales para t=0, x=0, dx/dt=v₀ calculamos la amplitud A y la fase inicial φ .

$\begin{array}{l} x = \frac{v_{0}}{ω_{0}} \sin ω_{0} t ω_{0} = \frac{B a}{\sqrt{m L}} \\ v = v_{0} \cos ω_{0} t \end{array}$

Siempre que la amplitud de la oscilación v₀/ω₀ no sea mayor que la longitud de la espira, de modo que la espira no esté completamente introducida en la región x≥ 0, la espira describirá un MAS con frecuencia angular ω₀ y periodo P=2π/ω₀.

La intensidad de la corriente vale

$i = \frac{B a}{L} x = v_{0} \sqrt{\frac{m}{L}} \sin (ω_{0} t)$

La máxima intensidad no depende de la anchura a de la espira, ni del campo magnético B.

Estudio energético

La energía cinética de la espira más la energía acumulada en la autoinducción en forma de campo magnético debe de ser constante e igual a la energía cinética inicial.

$\begin{array}{l} E_{k} = \frac{1}{2} m v^{2} = \frac{1}{2} m v_{0}^{2} \cos^{2} (ω_{0} t) \\ E_{L} = \frac{1}{2} L i^{2} = \frac{1}{2} \frac{B^{2} a^{2}}{L^{2}} x^{2} = \frac{1}{2} m v_{0}^{2} \sin^{2} (ω_{0} t) \\ E_{k} + E_{L} = \frac{1}{2} m v_{0}^{2} \end{array}$

Actividades

En el applet que viene a continuación, se estudia el comportamiento de una espira que viaja hacia una región (x≥ 0) en la que existe un campo magnético uniforme perpendicular al plano del applet: hacia adentro, negativo, en color azul claro o hacia fuera, positivo, en color rosa.

Se introduce

la intensidad B del campo magnético (T) un número positivo o negativo
la velocidad inicial v₀ (m/s)
La masa de la espira se ha fijado en m=0.1 kg
La anchura de la espira se ha fijado en a=0.25 m

Tenemos dos opciones

Resistencia R (en unidades 10^-3 Ω) no nula, autoinducción nula
Autoinducción L (en unidades 10^-5 H) no nula, resistencia nula.

Se pulsa el botón titulado Inicio para situar la espira en la posición de partida, y el botón Empieza para poner en movimiento la espira.

En la parte superior del applet, podemos observar el movimiento de la espira, su posición y velocidad en función del tiempo.

El sentido de la corriente inducida en la espira representada por el movimiento de puntos de color rojo.

La representación gráfica de la intensidad de la corriente inducida en función del tiempo, en la parte inferior derecha del applet. Se puede modificar la escala vertical de dicha representación actuando sobre la barra de desplazamiento titulada Escalas.

En un gráfico en forma de tarta, en la parte inferior del applet se efectúa el balance energético de este dispositivo electromecánico. Se representa la energía cinética de la espira (en color azul), la energía almacenada en forma de campo magnético en la autoinducción (en color rojo) y la energía disipada en la resistencia por efecto Joule (en color negro).

En el caso de que la espira tenga autoinducción no nula, el lado izquierdo de la espira estará siempre en la región x<0, en la que no hay campo magnético. Si se introduce una velocidad v₀ excesiva de la espira el programa no prosigue y nos invita a modificar el valor de la velocidad inicial de la espira. Para ello, la longitud de la espira ha de ser mayor que la amplitud v₀/ω₀ de las oscilaciones de la espira.

Ejemplo 1.

m=0.1 kg
a=0.25 m
B=0.1 T (hacia dentro)
v₀=2.0 m/s
R=0.5·10^-3 Ω
L=0

La constante de tiempo τ vale

$τ = \frac{R m}{B^{2} a^{2}} = \frac{0.5 \cdot 10^{- 3} \cdot 0.1}{{0.1}^{2} \cdot {0.25}^{2}} = 0.08$

La espira se introduce en la región en la que existe campo magnético.

En el instante t=0.2 s la velocidad de la espira es

$v = 2.0 \cdot \exp (- 0.2 / 0.08) = 0.16 m/s$

La posición del lado de la espira es

$x = 2 \cdot 0.08 (1 - \exp (- 0.2 / 0.08)) = 0.15 m$

La intensidad de la corriente en este instante vale

$i = \frac{B a v}{R} = \frac{0.1 \cdot 0.25 \cdot 0.16}{0.5 \cdot 10^{- 3}} = 8.21 A$

Como el flujo aumenta, la intensidad (en sentido antihorario) se opone al aumento de flujo

Ejemplo 2.

m=0.1 kg
a=0.25 m
B=0.1 T (hacia dentro)
v₀=2.0 m/s
R=0
L=8·10^-5 H

La frecuencia angular ω₀ del MAS vale

$ω_{0} = \frac{B a}{\sqrt{m L}} = \frac{0.1 \cdot 0.25}{\sqrt{0.1 \cdot 8 \cdot 10^{- 5}}} = 8.84 rad/s$

El semiperiodo, tiempo que tarda en entrar y salir la espira es P/2=π/ ω₀=0.36 s

La espira penetra hasta una distancia

$x_{m} = \frac{v_{0}}{ω_{0}} = \frac{2.0}{8.84} = 0.23 m$

La intensidad máxima en este instante es

$i_{m} = \frac{B a}{L} x_{m} = \frac{0.1 \cdot 0.25}{8 \cdot 10^{- 5}} 0.23 = 70.7 A$

SolenoideApplet aparecerá en un explorador compatible JDK 1.1

Referencias

Saslow W. M., Electromechanical implications of Faraday’s law: A problem collection. Am. J. Phys. 55 (11) November 1987, pp. 986-993.