• Inicio
• Electromagnetismo
• Campos dependientes del tiempo
• Inducción mutua y autoinducción

Sistema electro-mecánico oscilante

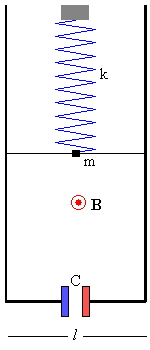Una varilla de masa m cuelga del techo sujeta por un muelle elástico de constante k. La varilla desliza sin fricción a lo largo de dos vías  paralelas colocadas en posición vertical separadas una distancia l. Las dos vías están unidas por la parte inferior mediante dos cables conectados un condensador de capacidad C. El conjunto está situado en una región donde hay un campo magnético B perpendicular al plano de las vías.

Movimiento en ausencia del campo magnético

Se cuelga un bloque de masa m de un muelle de constante k, que se deforma hasta que el peso del bloque mg se equilibra con la fuerza kx_e que ejerce el muelle, tal como se aprecia en la figura. Tomando como origen O la posición del extremo libre del muelle sin deformar, entonces x_e=-mg/k

 

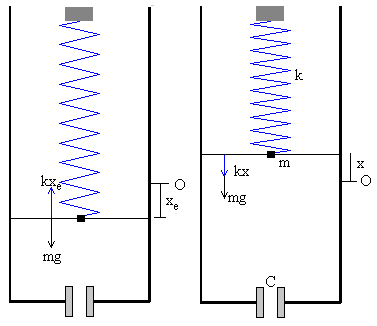
Si el bloque se suelta desde la posición x₀, el conjunto formado por el muelle y el bloque describe un Movimiento Armónico Simple (MAS). Las fuerzas que actúan sobre el bloque cuando se encuentra en la posición x son:

• El peso, mg

• La fuerza que ejerce el muelle, kx

La ecuación del movimiento es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-mg-kx}$

Haciendo el cambio de variable y=x+mg/k, obtenemos la ecuación diferencial

${\displaystyle \frac{d^{2}y}{d{t}^2}+{\omega }^{2}y=0\omega =\sqrt{\frac{k}{m}}}$

La solución de esta ecuación diferencial es el MAS

y=Asin(ωt+φ)
x=-mg/k+Asin(ωt+φ)
v=dx/dt=Aωcos(ωt+φ)

Las constantes A y φ se determinan a partir de las condiciones iniciales: en el instante t=0, la posición inicial es x₀, y la velocidad inicial es nula.

x=-mg/k+(x₀+mg/k)cos(ωt)
v=dx/dt=-(x₀+mg/k)·ωsin(ωt)

Balance energético

Tomando como nivel cero de energía potencial el origen O, cuando el muelle está sin deformar.

La energía inicial del sistema, teniendo en cuenta que el bloque parte en el instante t=0, de la posición x₀ con velocidad v=0, es la suma de

• La energía potencial gravitatoria

• La energía potencia elástica

${\displaystyle E=\frac{1}{2}k{x}_0^2+mg{x}_0}$

La energía del sistema en el instante t, cuando el bloque se encuentra en la posición x, y su velocidad es v, es la suma de tres términos:

• La energía potencial gravitatoria

• La energía potencia elástica

• La energía cinética del bloque

${\displaystyle E=\frac{1}{2}k{x}^2+mgx+\frac{1}{2}m{v}^2}$

Introduciendo las expresiones de la posición x, y de la velocidad v en función del tiempo, y después de hacer algunas operaciones algebraicas, comprobamos que la energía del sistema en el instante t es igual a la energía del sistema en el instante inicial.

Movimiento en presencia del campo magnético

Supongamos que el campo magnético B es perpendicular al plano de la página y apuntando hacia el lector,  y que la varilla se encuentra en el instante t, en la posición x, tal como se muestra en la figura.

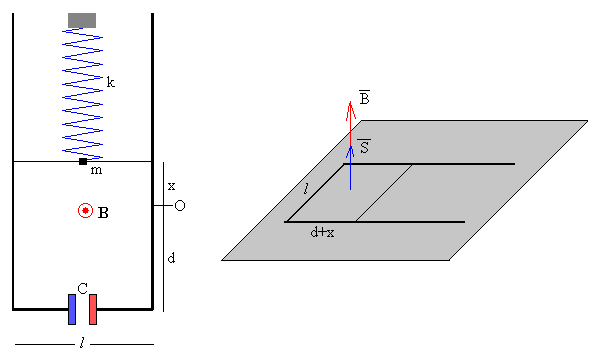
El flujo del campo magnético a través de la espira formada por la varilla y las vías es

Ф=B·S=B·l·(d+x)·cos0º

La fem inducida es

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}=-B·l\frac{dx}{dt}=-B·l·v}$

La carga del condensador es

q=C·V_є=-CBlv

La intensidad de la corriente en el circuito es

${\displaystyle i=\frac{dq}{dt}=-CBl\frac{dv}{dt}}$

El campo magnético B ejerce una fuerza sobre la corriente i dada por el producto vectorial

${\displaystyle F_m=i(u_t\times B)l}$

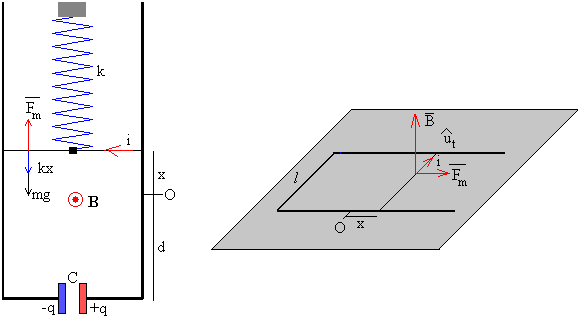
El módulo de la fuerza es F_m=iBl y su sentido está indicado en la figura.

Sobre la varilla actúan tres fuerzas

• El peso, mg

• La fuerza que ejerce el muelle deformado una longitud x,  kx

• La fuerza que ejerce el campo magnético sobre la corriente i que circula por la varilla F_m=iBl

La ecuación del movimiento de la varilla es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-mg-kx+iBl=-mg-kx-C{B}^2{l}^2\frac{dv}{dt}}$

o bien,

${\displaystyle \left(m+C{B}^2{l}^2\right)\frac{d^{2}x}{d{t}^2}+mg+kx=0}$

Haciendo el cambio de variable y=x+mg/k,

${\displaystyle \frac{d^{2}y}{d{t}^2}+{\omega }^{2}y=0\omega =\sqrt{\frac{k}{m+C{B}^2{l}^2}}}$

La solución de esta ecuación diferencial es la misma que la de una bloque unido a un muelle elástico, estudiado en el apartado anterior, salvo que la frecuencia angular es distinta.

y=Asen(ωt+φ)
x=-mg/k+Asin(ωt+φ)
v=dx/dt=Aωcos(ωt+φ)

Las constantes A y φ se determinan a partir de las condiciones iniciales: en el instante t=0, la posición inicial es x₀, y la velocidad inicial es nula.

x=-mg/k+(x₀+mg/k)cos(ωt)
v=dx/dt=-(x₀+mg/k)·ωsin(ωt) 

• La fem es

${\displaystyle V_{\epsilon }=-B·l·v=Bl\left(x_0+\frac{mg}{k}\right)\omega \sin (\omega t)}$

• La intensidad

${\displaystyle i=\frac{dq}{dt}=-CBl\frac{dv}{dt}=CBl\left(x_0+\frac{mg}{k}\right){\omega }^2\text{cos}(\omega t)}$

La intensidad está adelantada 90º respecto de la fem

• La carga del condensador es

${\displaystyle q=-CBlv=CBl\left(x_0+\frac{mg}{k}\right)\omega \sin (\omega t)}$

Balance energético

Teniendo en cuenta que la varilla parte en el instante t=0 de la posición x₀ con velocidad v=0, y que el condensador se encuentra descargado, la energía inicial del sistema es la suma de

• La energía potencial gravitatoria

• La energía potencia elástica

${\displaystyle E=\frac{1}{2}k{x}_0^2+mg{x}_0}$

La energía del sistema en el instante t, cuando la posición del bloque es x, y su velocidad es v es la suma de cuatro términos

• La energía potencial gravitatoria

• La energía potencial elástica

• La energía cinética de la varilla

• La energía del condensador cargado

${\displaystyle E=\frac{1}{2}k{x}^2+mgx+\frac{1}{2}m{v}^2+\frac{1}{2}\frac{q^2}{C}}$

Introduciendo las expresiones de la posición x, y de la velocidad v y de la carga q del condensador en función del tiempo, y después de hacer algunas operaciones algebraicas, comprobamos que la energía del sistema en el instante t es igual a la energía del sistema en el instante inicial t=0.

Actividades

Se pulsa el botón titulado Inicio.

• Con el puntero del ratón se mueve la flecha horizontal de color rojo, para establecer la posición inicial entre 5 y -20 cm

Se introduce

• El campo magnético B, actuando en la barra de desplazamiento titulada Campo magnético

• La capacidad C del condensador, en unidades de 10^-3 F, actuando en la barra de desplazamiento titulada Capacidad

• La masa de la varilla se ha fijado en m=0.001 kg

• La constante elástica del muelle se ha fijado en k=0.1 N/m

• La longitud de la varilla se ha fijado en l=25 cm=0.25 m

Se pulsa el botón titulado Empieza

Se observa el movimiento de la varilla deslizando a lo largo de las vías paralelas

El sentido de la corriente se pone de manifiesto, mediante el movimiento de puntos de color rojo, que representan a los portadores de carga positiva.

La intensidad de los colores azul y rojo, representa la cantidad de carga en la placa negativa y positiva del condensador, respectivamente.

En la parte central del applet, un diagrama de barras representa la energía del sistema y su distribución:

• En color azul la energía potencial elástica del muele deformado, kx²/2

• En color rojo, la energía almacenada en el condensador en forma de campo eléctrico, q²/(2C)

• En color gris claro, la energía cinética de la varilla, mv²/2

• En color gris oscuro, la energía potencial gravitatoria de la varilla, mgx. Esta energía puede se positiva o negativa dependiendo de la posición de la varilla, x>0 por encima del origen,  x<0, por debajo del origen.

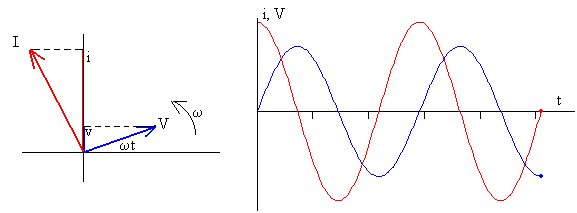
Finalmente, se representa la fem V_є, y la intensidad de la corriente i. La segunda como vemos, está adelantada 90º respecto de la primera.

En la simulación se introducen valores inusualmente altos de la capacidad del orden de 10^-3 F, y del campo magnético del orden de 1 T.

Ejemplo:

C=2·10^-3 F
B=3 T, (apuntando hacia el lector)
k=0.1 N/m
m=0.001 kg
l=0.25 m
Con el puntero del ratón establecemos la posición inicial de la varilla, x₀=0.05 m

En ausencia de campo magnético, el sistema formado por el muelle y la varilla oscilaría con una frecuencia angular de

${\displaystyle \omega =\sqrt{\frac{k}{m}}\omega =\sqrt{\frac{\text{0}\text{.1}}{\text{0}\text{.001}}}=10\text{rad/s}}$

El periodo P=2π/ω=0.63 s

Si situamos el dispositivo en una región donde hay un campo magnético uniforme, la frecuencia angular del MAS es

${\displaystyle \omega =\sqrt{\frac{k}{m+C{B}^2{l}^2}}\omega =\sqrt{\frac{\text{0}\text{.1}}{\text{0}\text{.001}+{\text{2·10}}^{\text{-3}}·3^2·{0.25}^2}}=6.86\text{rad/s}}$

El periodo es P=0.92 s

En el instante t=P/4=0.23 s

• La posición de la varilla es

x=-mg/k+(x₀+mg/k)cos(ωt)

${\displaystyle x=-\frac{0.001·9.8}{0.1}+\left(0.05+\frac{0.001·9.8}{0.1}\right)\cos (6.86·0.23)=-0.098\text{m}}$

•  La velocidad de la varilla es

v=dx/dt=-(x₀+mg/k)·ωsin(ωt)

${\displaystyle v=-\left(0.05+\frac{0.001·9.8}{0.1}\right)·6.86·\sin (6.86·0.23)=-1.015\text{m/s}}$

• La fem producida en el circuito es

${\displaystyle \begin{array}{l}{V}_{\epsilon }=Bl\left(x_0+\frac{mg}{k}\right)\omega \sin (\omega t)\\ V_{\epsilon }=3·0.25·\left(0.05+\frac{0.001·9.8}{0.1}\right)·6.86·\sin (6.86·0.23)=0.76\text{V}\end{array}}$

La amplitud de la fem es 0.76 V

• La intensidad de la corriente es

${\displaystyle \begin{array}{l}i=CBl\left(x_0+\frac{mg}{k}\right){\omega }^2\text{cos}(\omega t)\\ i=2·{10}^{-3}·3·0.25·\left(0.05+\frac{0.001·9.8}{0.1}\right)·{6.86}^2·\text{cos}(6.86·0.23)=0\text{A}\end{array}}$

La amplitud de la intensidad es 0.01 A

• La carga del condensador es

${\displaystyle \begin{array}{l}q=CBl\left(x_0+\frac{mg}{k}\right)\omega \sin (\omega t)\\ q=2·{10}^{-3}·3·0.25·\left(0.05+\frac{0.001·9.8}{0.1}\right)·6.86·\sin (6.86·0.23)=1.52·{10}^{-3}\text{C}\end{array}}$

Balance energético

Como la varilla parte en el instante t=0, de la posición x=0.05 m con velocidad v=0. La energía inicial del sistema es la suma de

• La energía potencial elástica

E_e=kx²/2=0.1·0.05²/2=1.25·10^-4 J

• La energía potencial gravitatoria

E_g=mgx=0.001·9.8·0.05=4.9·10^-4 J

La energía total inicial es

E=E_e+E_g=6.15·10^-4 J

La energía del sistema en el instante t=0.23 s, es la suma de

• La energía potencial elástica debida a la deformación del muelle

E_e=kx²/2=0.1·(-0.098)²/2=4.8·10^-4 J

• La energía potencial gravitatoria

E_g=mgx=0.001·9.8·(-0.098)=-9.6·10^-4 J

• La energía cinética de la varilla

E_k=mv²/2=0.001·(-1.015)²=5.15·10^-4 J

• La energía acumulada en el condensador en forma de campo eléctrico

E_c=q²/(2C)=(1.52·10^-3)²/(2·2·10^-3)=5.80·10^-4 J

La energía total es

E=E_e+E_g+E_k+E_c=6.15·10^-4 J

SolenoideApplet aparecerá en un explorador compatible JDK 1.1

Se mueve con el puntero del ratón la flecha de color rojo

Referencias

Awesome oscillations. Physics challenges for teachers and students. The Physics Teacher, Vol. 42, May 2004, pp 2

Curso Interactivo de Física en Internet © Ángel Franco García