• Inicio
• Electromagnetismo
• Campos dependientes del tiempo
• Inducción mutua y autoinducción

Circuito LCR conectado a una batería

En esta página, se estudia el comportamiento de un circuito LCR conectado a una batería. Se estudia el estado transitorio y su evolución hacia el estado estacionario después de un cierto tiempo teóricamente infinito, pero que en la práctica viene determinado por el valor de la constante γ.

Uno de los aspectos más interesantes de este circuito es que la diferencia de potencial en el condensador puede ser mayor que el de la batería.

Ecuación del circuito

Consideremos el siguiente circuito formado por un condensador de capacidad C, una resistencia R, una autoinducción L y una batería de fem V₀ sin resistencia interna.

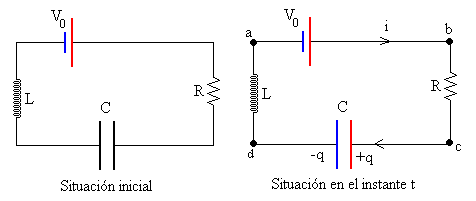
El condensador está inicialmente descargado. En el instante t=0, se cierra el circuito. En un instante dado t, tendremos que

• El condensador C tiene una carga q
• Por la resistencia R circula una corriente de intensidad i.
• Por la autoinducción L circula una corriente de intensidad i.

Medimos las diferencias de potencial entre los puntos a y b, b y c, c y d, d y a. 

La ecuación del circuito será

V_ab+V_bc+V_cd+ V_da =0

• En la batería el potencial del polo negativo a es menor que el polo positivo b, de modo que V_ab=-V₀
• En la resistencia R la corriente de intensidad i circula de b a c, luego V_bc=iR
• En el condensador C el potencial de c (placa positiva) es mayor que el a (placa negativa), de modo que V_cd=q/C
• En la autoinducción es equivalente a una batería que se está cargando, ya que se opone a que aumente la intensidad. La diferencia de potencial entre d y a es igual a la fem autoinducida V_L cambiada de signo.

${\displaystyle V_L=-L\frac{di}{dt}}$

La ecuación del circuito es

${\displaystyle -V_0+iR+\frac{q}{C}+L\frac{di}{dt}=0}$

Con i=dq/dt.

${\displaystyle \begin{array}{l}\frac{d^{2}q}{d{t}^2}+\frac{R}{L}\frac{dq}{dt}+\frac{1}{LC}q=\frac{V_0}{L}\\ \frac{d^{2}q}{d{t}^2}+2\gamma \frac{dq}{dt}+{\omega }_0^{2}q=\frac{V_0}{L}\end{array}}$

La solución de esta ecuación diferencial es de la forma

${\displaystyle q=y_1+\exp (-\gamma t)(A·\sin \omega t+B·\cos \omega t){\omega }^2={\omega }_0^2-{\gamma }^2}$

La primera y₁ una constante, es la solución particular y la segunda la solución general que ya encontramos en el estudio de las oscilaciones amortiguadas γ<ω₀.

Introduciendo la solución particular y₁ en la ecuación diferencial tenemos que

y₁=CV₀

Inicialmente el condensador C está descargado q=0, y la intensidad i=dq/dt es cero.

Las condiciones iniciales q=0, y dq/dt=0 determinan las constantes A y B. Después de hacer algunas operaciones tenemos que

${\displaystyle \begin{array}{l}q=C{V}_0\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\sin \omega t+\cos \omega t\right)\right)\\ i=\frac{dq}{dt}=\frac{V_0}{L\omega }\exp (-\gamma t)\sin \omega t\end{array}}$

Comprobamos que en el instante t=0, q=0 e i=0, y que para t→∞,

${\displaystyle q\to C{V}_0}$

Diferencia de potencial en los extremos de cada uno de los elementos del circuito

• En la batería el potencial del polo negativo a es menor que el polo positivo b, de modo que

V_ab=-V₀

• En la resistencia R la corriente de intensidad i circula de b a c, luego

${\displaystyle V_{bc}=iR=V_0\frac{2\gamma }{\omega }\exp (-\gamma t)\sin (\omega t)}$

• En el condensador C el potencial de c (placa positiva) es mayor que el a (placa negativa), de modo que

${\displaystyle V_{cd}=\frac{q}{C}=V_0\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\text{sin(}\omega t)+\cos (\omega t)\right)\right)}$

• En la autoinducción es equivalente a una batería que se está cargando, ya que se opone a que aumente la intensidad. La diferencia de potencial entre d y a es.

${\displaystyle V_{da}=L\frac{di}{dt}=V_0\exp (-\gamma t)\left(\text{cos(}\omega t)\text{-}\frac{\gamma }{\omega }\text{sin(}\omega t)\right)}$

Estudio energético

• La energía almacenada en el condensador en forma de campo eléctrico es

${\displaystyle U_C=\frac{1}{2}\frac{q^2}{C}=\frac{1}{2}C{V}_0^2{\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\sin (\omega t)+\cos (\omega t)\right)\right)}^2}$

• La energía almacenada en la autoinducción en forma de campo magnético es

${\displaystyle U_L=\frac{1}{2}L{i}^2=\frac{1}{2}\frac{V_0^2}{L{\omega }^2}\exp (-2\gamma t){\sin }^{\text{2}}(\omega t)}$

• La energía disipada en la resistencia es

${\displaystyle \begin{array}{l}{U}_R={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R·dt=\frac{R{V}_0^2}{L^2{\omega }^2}{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-2\gamma t){\text{sin}}^{\text{2}}(\omega t)dt}}=\frac{R{V}_0^2}{2L^2{\omega }^2}{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-2\gamma t)(1-\cos (2\omega t))dt}=\\ \frac{R{V}_0^2}{4L^2{\omega }^2}\left\{\frac{1}{\gamma }\left(1-\exp (-2\gamma t)\right)-\frac{1}{{\omega }_0^2}\left(\exp (-2\gamma t)(\omega ·\sin (2\omega t)-\gamma \cos (2\omega t))+\gamma \right)\right\}\end{array}}$

Se integra por partes, para llegar a la expresión final se tiene en cuenta que ${\omega }^2={\omega }_0^2-{\gamma }^2$

• La energía suministrada por la batería es

${\displaystyle \begin{array}{l}{U}_V={\displaystyle \underset{0}{\overset{t}{\int }}{V}_{0}i·dt}=\frac{V_0^2}{L\omega }{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-\gamma t)\sin (\omega t)·dt}=\\ V_0^{2}C\left(1-\exp (-\gamma t)(\cos (\omega t)+\frac{\gamma }{\omega }\sin (\omega t)\right)\end{array}}$

Se puede comprobar la conservación de la energía

U_V=U_C+U_L+U_R

Una parte de la energía suministrada por la batería se almacena en el condensador, otra parte en la autoinducción y el resto se disipa en la resistencia.

Después de un tiempo t→∞

• La carga en el condensador tiende a CV_0, la energía almacenada en el condensador es

${\displaystyle U_C=\frac{1}{2}C{V}_0^2}$

• La intensidad tiende a cero, no hay energía almacenada en la autoinducción

U_L=0

• La energía disipada en la resistencia tiende a

${\displaystyle U_R=\frac{R{V}_0^2}{4L^2{\omega }^2}\left\{\frac{1}{\gamma }-\frac{\gamma }{{\omega }_0^2}\right\}=\frac{R{V}_0^2}{4L^2{\omega }^2}\frac{{\omega }^2}{\gamma {\omega }_0^2}=\frac{1}{2}C{V}_0^2}$

• La energía suministrada por la batería tiende a

U_V=CV₀

La mitad de la energía suministrada por la batería se almacena como energía del campo eléctrico en el condensador y la otra mitad se disipa en la resistencia. El mismo resultado obtenido en la carga del condensador sin autoinducción

Actividades

Se introduce

• El coeficiente de autoinducción L en H, en el control del edición titulado Autoinducción

• La capacidad del condensador C en nF (10^-9), en el control de edición titulado Capacidad.

• La resistencia R en kΩ (10³), en el control de edición titulado Resistencia.

• La fem de la batería se ha fijado en V₀=4 V

Se pulsa el botón titulado Empieza

Se representa, la diferencia de potencial en los extremos de

• La batería (se toma como valor positivo)

• En el condensador

• En la autoinducción

• En la resistencia

Observamos el estado transitorio y su evolución hacia el estado estacionario, cuando t→∞

Si aumentamos la resistencia, se tarda menos tiempo en alcanzar aproximadamente el estado estacionario.

El circuito estudiado en el artículo citado en las referencias consta de

• Una resistencia, R=1.044·10³ Ω

• Un condensador, C=9.66·10^-9 F

• Autoinducción, L=9.44 H

• Batería V₀=4.04 V

La frecuencia del circuito vale

${\displaystyle {\omega }^2={\omega }_0^2-{\gamma }^2=\frac{1}{LC}-\frac{R^2}{4L^2}}$

ω₀=3311.5 rad/s
γ=55.3 s^-1

Estamos en la situación descrita en esta página (amortiguada) γ< ω₀

LineasApplet aparecerá en un explorador compatible JDK 1.1

Referencias

Faleski M. C. Transient behaviour of the driven RLC circuit. Am . J. Phys. 74 (5) May 2006, pp. 429-437

Curso Interactivo de Física en Internet © Ángel Franco García