El prisma de vidrio

Índice de refracción de un prisma. Laboratorio de Física. E.U. Ingeniería Técnica de Minas y Obras Públicas (Barakaldo)

El prisma es un instrumento de gran importancia en la historia de la Óptica. Newton demostró con el prisma que la luz blanca es una mezcla de varios colores y que la refracción depende del color tal como se aprecia en la figura.

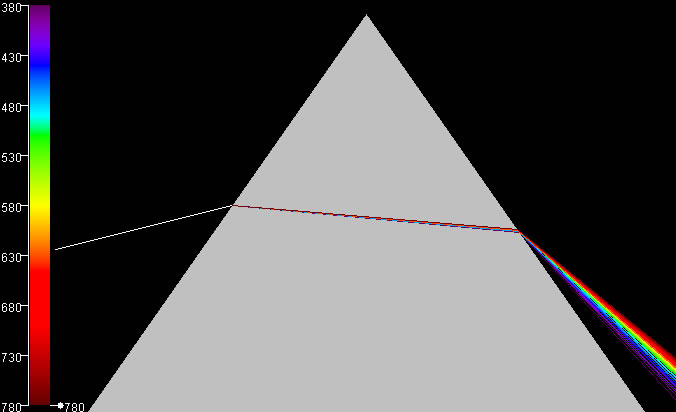
En el programa interactivo al final de la página, se elige un color (una frecuencia o longitud de onda) y se traza el camino seguido por el rayo de luz que atraviesa el prisma. Se mide el ángulo de desviación y se determina el índice de refracción del vidrio para el color elegido.

Geometría del prisma

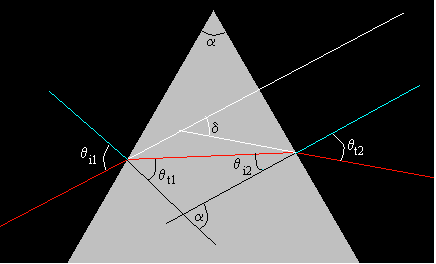
En al figura, se muestra un prisma de ángulo α hecho de un vidrio que tiene un índice de refracción n. Un rayo de luz de color rojo incide sobre la cara izquierda del prisma. El ángulo que forma el rayo incidente con la normal es θ_i1. Aplicamos la ley de Snell para trazar el rayo refractado

sinθ_i1=n·sin θ_t1.

θ_t1 es el ángulo que forma el rayo refractado con la normal a la cara izquierda del prisma. El rayo se ha desviado (θ_i1- θ_t1)

El rayo refractado llega a la cara derecha del prisma formado un ángulo θ_i2con la normal. Aplicamos la ley de Snell para obtener la dirección del rayo refractado

n·sinθ_i2=sin θ_t2.

El rayo se ha desviado (θ_t2- θ_i2)

El ángulo que forma la prolongación del rayo incidente con el rayo que sale del prisma se denomina ángulo de desviación.

δ=(θ_i1- θ_t1)+ (θ_t2- θ_i2)= θ_i1+ θ_t2-α

ya que α= θ_t1+ θ_i2

Escribimos el ángulo de desviación δ en términos del ángulo de incidencia θ_i1, del índice de refracción n, y del ángulo del prisma α. Después de hacer algunas operaciones llegamos a la expresión

$δ = θ_{i 1} + \arcsin (\sin α \sqrt{n^{2} - \sin^{2} θ_{i 1}} - \sin θ_{i 1} \cos α) - α$

En la figura, se representa el ángulo de desviación δ en función del ángulo de incidencia θ_i1.

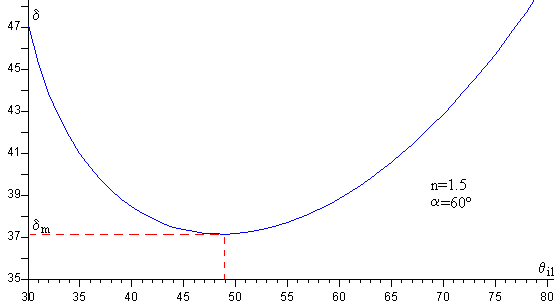
Mínima desviación

El ángulo de desviación presenta un mínimo δ_m para un cierto valor del ángulo de incidencia θ_i1. El mínimo se calcula igualando la derivada de δ respecto de θ_i1, a cero

$\frac{d δ}{d θ_{i 1}} = 0$

Derivando la expresión anterior obtenemos una expresión muy larga, difícil de simplificar. Vamos a calcular la desviación mínima de otra forma, tal como se describe en el libro citado en las referencias. Como

$\begin{array}{l} δ = θ_{i 1} + θ_{t 2} - α \\ \frac{d δ}{d θ_{i 1}} = 1 + \frac{d θ_{t 2}}{d θ_{i 1}} = 0 \end{array}$

De la aplicación de la ley de Snell a ambas caras del prisma tenemos las siguientes relaciones:

sinθ_i1=n·sin θ_t1.
cosθ_i1·dθ_i1=n·cos θ_t1·dθ_t1

n·sinθ_i2=sin θ_t2.
n·cosθ_i2·dθ_i2=cos θ_t2·dθ_t2

Como α= θ_t1+ θ_i2
dθ_t1=- dθ_i2

Combinando estas expresiones, obtenemos

$\frac{d θ_{t 2}}{d θ_{i 1}} = - \frac{\cos θ_{i 1} \cdot \cos θ_{i 2}}{\cos θ_{t 1} \cdot \cos θ_{t 2}}$

Finalmente, de la condición de mínimo

$\begin{array}{l} 1 - \frac{\cos θ_{i 1} \cdot \cos θ_{i 2}}{\cos θ_{t 1} \cdot \cos θ_{t 2}} = 0 \frac{\cos θ_{i 1}}{\cos θ_{t 2}} = \frac{\cos θ_{t 1}}{\cos θ_{i 2}} \\ \frac{1 - \sin^{2} θ_{i 1}}{1 - \sin^{2} θ_{t 2}} = \frac{1 - \sin^{2} θ_{t 1}}{1 - \sin^{2} θ_{i 2}} \end{array}$

Aplicando la ley de Snell

$\frac{1 - \sin^{2} θ_{i 1}}{1 - \sin^{2} θ_{t 2}} = \frac{1 - \frac{1}{n^{2}} \sin^{2} θ_{i 1}}{1 - \frac{1}{n^{2}} \sin^{2} θ_{t 2}}$

Como n≠1, la relación anterior es cierta para θ_i1=θ_t2 por lo que θ_i2=θ_t1

Cuando la desviación δ es mínima, el rayo atraviesa el prisma horizontalmente, tal como se muestra en la figura.

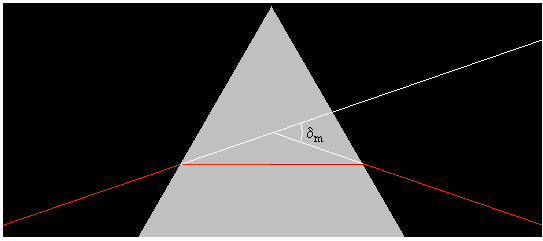
Como α= θ_t1+ θ_i2y δ=θ_i1+ θ_t2-α

$\begin{array}{l} δ_{m} = 2 θ_{i 1} - α \\ α = 2 θ_{t 1} \end{array}$

Aplicando la ley de Snell

$\begin{array}{l} \sin θ_{i 1} = n \cdot \sin θ_{t 1} \\ \sin (\frac{δ_{m} + α}{2}) = n \sin (\frac{α}{2}) \\ δ_{m} = 2 \arcsin (n \cdot \sin (\frac{α}{2})) - α \end{array}$

El ángulo de incidencia θ_i1 para el cual se produce la desviación mínima es

$θ_{i 1} = \frac{δ_{m} + α}{2}$

Midiendo el ángulo de desviación mínima δ_m obtenemos el índice de refracción de la sustancia transparente. Para medir el índice de refracción de líquidos o gases se construye un prisma hueco cuyos lados son vidrios planos-paralelos, el hueco se llena con el líquido o con el gas a presión.

Ejemplo:

Medimos el ángulo de desviación δ para calcular el índice de refracción del prisma n.

$\begin{array}{l} δ = θ_{i 1} + \arcsin (\sin α \sqrt{n^{2} - \sin^{2} θ_{i 1}} - \sin θ_{i 1} \cos α) - α \\ n^{2} = \sin^{2} θ_{i 1} + {(\frac{\sin (δ - θ_{i 1} + α) + \sin θ_{i 1} \cos α}{\sin α})}^{2} \end{array}$

Angulo del prisma, α=60º
Angulo de incidencia, θ_i1=40º
Ángulo de desviación para la luz roja λ=640 nm, δ=39.44º

$\begin{array}{l} n^{2} = \sin^{2} 40 + {(\frac{\sin (39.44 - 40 + 60) + \sin 40 \cos 60}{\sin 60})}^{2} \\ n = 1.50917 \end{array}$

Medimos el ángulo de desviación mínima δ_m para calcular el índice de refracción del prisma n.

Cambiamos el ángulo de incidencia grado a grado hasta encontrar la desviación mínima.

Angulo de incidencia, θ_i1=49º.
Ángulo de desviación mínima, δ_m=37.98º

Comprobamos que el programa interactivo proporciona un valor correcto de la desviación mínima

$θ_{i 1} = \frac{δ_{m} + α}{2} 49 = \frac{δ_{m} + 60}{2} δ_{m} \approx 38 º$

Calculamos el índice de refracción

$n = \frac{\sin (\frac{δ_{m} + α}{2})}{\sin (\frac{α}{2})} n = \frac{\sin (\frac{37.98 + 60}{2})}{\sin (\frac{60}{2})} = 1.5092$

Actividades

Se introduce

El ángulo del prisma α, actuando en la barra de desplazamiento titulada Angulo prisma.
El ángulo incidente θ_i1, actuando en la barra de desplazamiento titulada Angulo incidente.

Se pulsa el botón titulado Nuevo

Se selecciona la longitud de onda de la luz moviendo con el puntero del ratón el pequeño círculo de color negro situado al lado de la representación del espectro visible.

Fijamos la longitud de onda y cambiamos el ángulo de incidencia, hasta encontrar el valor de la desviación mínima. A partir de este dato, calculamos el índice de refracción.

Fijamos el ángulo de incidencia y medimos el ángulo de desviación δ₁ para la primera longitud de onda λ₁=380 nm y el ángulo de desviación δ₂ para la última λ₂=780 nm del espectro visible. De este modo, calculamos el ángulo δ₁-δ₂ que se aprecia en la segunda figura de esta página.

Nota: los índices de refracción del prisma para cada longitud de onda del espectro visible se calculan empleando un polinomio de grado tres que mejor ajusta a los datos que se dan en la tabla más abajo.

Mueva con el puntero del ratón el pequeño círculo de color negro a la izquierda del applet

Indice de refracción

El índice de refracción n no es constante, sino que depende de la longitud de onda o de la frecuencia de la luz con la que se ilumina el prisma.

Por ejemplo, el índice de refracción del vidrio denominado Borosilicate Crown para las longitudes de onda del espectro visible, se proporcionan en la siguiente tabla.

Color	Longitud de onda nm	Indice de refracción
Rojo	640	1.50917
Amarillo	589	1.51124
Verde	509	1.51534
Azul	486	1.51690
Violeta	434	1.52136

Fuente: hypertextbook.com/facts/2005/JustinChe.shtml (junio 2008)

Para calcular el índice de refracción para cualquier otra longitud de onda del espectro visible se ajusta los datos de la tabla mediante el procedimiento de los mínimos cuadrados a un polinomio de grado m.

En el siguiente programa interactivo, se representan los datos experimentales mediante puntos de color rojo.

Se introduce

El grado del polinomio en el control de selección titulado Grado polinomio.

Se pulsa el botón titulado Calcula

Se representa el polinomio que mejor ajusta, en color azul.

Moviendo con el puntero del ratón el pequeño círculo de color negro situado en el eje horizontal, podemos obtener los valores del índice de refracción de la longitud de onda seleccionada.

Mueva con el puntero del ratón el pequeño círculo de color negro situado en el eje horizontal

Referencias

Hetch-Zajac. Optica. Addison-Wesley Iberoamericana (1986), págs. 138-139