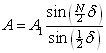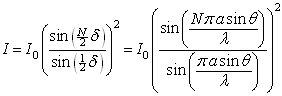Uhinak

Interferentzia 
eta difrakzioa

Quincke-ren hodia

Uhinen interferentzia
bi iturrirekin (I)

Uhinen interferentzia
bi iturrirekin (II)

Uhinen interferentzia
zenbait iturrirekin

Zirrikitu lineal batek
sortutako difrakzioa

Interferentzia
gehi difrakzioa

Difrakzioa, irekigune
laukizuzenarekin
eta zirkularrarekin

Fresnelen difrakzioa

Anplitudea eta intentsitatea

Diagrama polarra

Saiakuntza

Deskribapena

Azter dezagun orain uhinen interferentzia, baina zenbait iturri harmoniko eta sinkrono erabiliz (bi baino gehiago). Sinplifikatzeko, koka ditzagun iturriok lerro zuzen batean, denak "a" separazio berdinarekin, alboko irudiak erakusten duen bezala. Kalkula dezagun uhin multzo horren gainezarketa, iturrietatik nahikoa urrun dagoen P puntu batean (separazioarekin alderatuta). Iturri bakar batek uhina igortzen duenean, P puntuak HHS deskribatzen du w maiztasun angeluarraz eta A1 anplitudeaz. Iturri guztiek batera igortzen dutenean (N), P puntuak deskribatzen duen higidura N HHS gainezarrita, norabide berean eta maiztasun berdinekin.

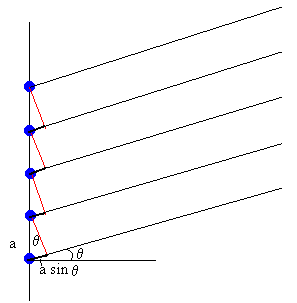
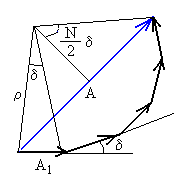
Anplitude erresultantea kalkulatzeko (A), batu ditzagun iturri guztien anplitudeak baina bektorialki, alegia, desfaseak kontutan hartuta. Iturri guztiek anplitude bera badute, bektore guztiek modulu bera dute (A₁) eta bi bektore kontsekutiboren arteko desfaseari dei diezaiogun d. Bi iturriren kasuan bezalaxe, desfase hori izango da k, uhin-zenbakia, bider distantzien arteko diferentzia, a sinq.

d =ka·sinq .

Ondoko irudiaren laguntzaz bektore horien batura kalkula daiteke (irudian bost), denak anplitude berekoak (A1) eta desfase konstantekoak (d): bektore bakoitza aurrekoaren erpinean kokatuta poligonal bat lortzen da, eta A anplitude erresultantea urdinez adierazten dena. Hona hemen geometrikoki lortzen diren erlazioak:

Hemen r deitu diogu poligono erregularraren erradioari. Bi ekuazio horietatik r eliminatzen badugu, A anplitude erresultantea berridatz daiteke A₁ anplitudearen menpe:

Eta intentsitatea anplitudearen karratuaren proportzionala da:

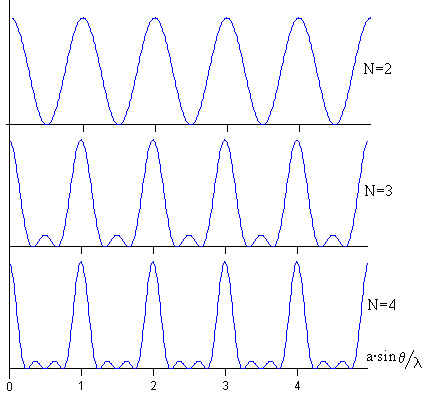
Interferentzia eraikitzailea izateko: a·sinθ=nλ . Eta n zenbaki osoa. Ondoz-ondoko iturriek igorritako uhinak fasean iristen dira gainezartze puntura. Kasu horretan, I intentsitatearen adierazpeneko izendatzailea eta zenbatzailea, biak, nuluak dira (0/0), baina zatidura horren  indeterminazioak, L´Hôpital-en erregela aplikatuz, "N ²" ematen du, alegia, intentsitateak honako balioa du: I=N ²I₀ eta maximoa da, maximo nagusia.

Aldiz, intentsitatea nulua izateko (I=0) zenbakitzailea nulua izan behar da baina izendatzailea ordea ez. Esate baterako, N=4 iturri badira, minimoak agertzen dira honako baldintzetan: (bat): 4πa·sinθ/λ=π , (bi): 4πa·sinθ/λ=2π, (eta hiru): 4πa·sinθ/λ=3π. Hau da, a·sinθ=λ/4, a·sinθ=λ/2, eta  a·sinθ=3λ/4, beheko irudiak erakusten duen bezala eta geroagoko appletak ere.

Oro har, I intentsitatea minimoa da honako baldintza betetzen duten posizioetan: a·sinθ=n'λ/N. Eta hemen n' ez da edozein zenbaki oso, baizik eta soilik 1-etik (N-1)-eraino. Ondoren (N+1)-etik (2N-1)-eraino, eta abar. Izan ere, n'=N, 2N, 3N ... ez dira minimoak, izendatzailea baliogabetzeaz gain, zenbakitzailea ere baliogabetzen dutelako eta hori maximoa da, maximo nagusia. Bi minimoren artean beti dago maximo bat (sekundarioa), hortaz N-2 maximo sekundario daude bi maximo nagusiren artean. Maximo sekundarioen intentsitatea txikia da, batez ere N handia denean.

Irudiak erakusten du I intentsitatearen adierazpena, a·sinθ/λ aldagaiaren menpe, eta iturri-kopuru ezberdinetarako: N =2, 3 eta 4. Iturri-kopurua handitu ahala, intentsitatearen gailurrak gero eta estuagoak dira, eta maximo sekundarioak gero eta txikiagoak. Halaber, N oso handia denean intentsitate erresultantea soilik maximo nagusietan kontzentratzen da (a·sinθ/λ=n), eta posizio horretatik kanpo ia nulua da.

Ezagutzen baditugu, uhinen λ uhin-luzera eta iturrien arteko a separazioa, erraz kalkulatzen da zein posizio angeluarretan (θ) sortzen diren interferentziazko maximo nagusiak edota minimoak.

Anplitudea eta intentsitatea interferentzian

Aukeran idatz daiteke:

• Iturri kopurua, N, zerrenda tolesgarrian aukeratuz.

Ondoren, Irudia botoia klikatu.

Leihatilaren eskumako aldean, grafikoki, intentsitate erresultantea adierazten da honako aldagaiaren menpe: x=a·sinθ/λ. Azpiko aldean, intentsitate erresultantea, baina gris-eskalan adierazita, argazkia balitz bezalaxe. Horrelakoxeak izaten dira interferentzia diagramak argiarekin egiten direnean.

Ardatz horizontalean dagoen laukitxo gorria saguarekin klikatuz desplaza daiteke, ezker-eskuin, eta laukitxoaren posizioaren arabera, leihatilaren ezkerraldean adierazten dira, bektorialki, iturri bakoitzaren uhinen anplitudeak eta faseak, eta anplitude eta fase erresultantea. Halaber, goiko eta ezkerreko erpinean idatziz ematen dira x posizioa eta intentsitate erresultantea, maximo nagusiarena unitatetzat hartuta.

Laukitxo gorria maximo nagusi batean kokatzen dugunean, bektore guztiek (N bektore) norabide eta noranzko bera dute, anplitude erresultantea N bider handiagoa da eta, beraz, intentsitatea N ² bider.

Minimo batean kokatzen dugunean, berriz, lehen bektorearen jatorria eta azken bektorearen erpina justu puntu berean daude, anplitude erresultantea nulua da eta intentsitatea ere bai.

Applet honetan egiazta daitezke, interferentziaren ondorioz lortzen diren intentsitate maximoko eta minimoko posizio guztiak, baina iturri-kopurua txikia denean: N=2, 3, 4, eta 5.

Diagrama polarra

Diagrama polarrak ere interferentziaren intentsitatea adierazten du θ angeluaren menpe, baina beste ikuspegi batetik.

Demagun lau iturri ditugula (N=4), eta haien arteko separazioa dela: a=λ/2, justu uhin-luzeraren erdia. Intentsitate maximoa lortzen duten norabideak honakoak dira: a·sinθ/λ=n , alegia sinθ=2n. Ekuazio horrek soluzio errealak ematen ditu soilik n=0 bada, hau da, θ=0 eta π. Aldiz, intentsitatearen minimoak lortzen dira a·sinθ/λ=n'/N, hau  da, sinθ=n'/2 eta n'=1, 2, 3, 5, 6... baina soilik dira posibleak n'=±1, eta  n'=±2  eta horiei dagozkien angeluak honakoak dira: θ=π/6 eta π/2.

Lau antena kokatzen baditugu, eta euren arteko separazioa uhin-luzeraren erdia bada, uhinak igorri eta jaso egiten dira, batez ere, antenak lotzen dituen zuzenaren norabide perpendikularrean.

Saiakuntza

Aukeran idatz daitezke:

• a/λ erlazioa, alegia, uhin-iturrien arteko separazioa zati uhin luzera, dagokion kontrolean idatziz.
• Iturri-kopurua zerrenda tolesgarrian aukeratuz (2-tik 10 arte).
• Irudia marrazteko Eskala desplazamendu-barrari saguaz eragiten (10-etik 100 arte).

Azkenik, Irudia botoia klikatu.

Leihatilaren goiko eta ezkerreko erpinean, programak maximo nagusien norabideak idatziz ematen ditu.

Maximo sekundarioak ikusteko, irudiaren eskala handitu behar da.

Saiakuntza

Aukeran idatz daitezke:

• Uhin luzera, λ, desplazamendu-barrari saguaz eragiten.
• Uhin-iturrien arteko separazioa, a, desplazamendu-barrari saguaz eragiten.
• Iturri-kopurua, zerrenda tolesgarrian zenbaki bat aukeratuta.

Irudia botoia klikatu.

Hasteko, iturri kopurua aukeratzerakoan, 1 bakarra aukeratzen badugu, uhin zirkularrak behatzen dira iturriaren inguruan simetrikoki sakabanatuta (gorriz). Bi eskualde zuri kontsekutiboren arteko distantzia uhin luzera da, edota bi eskualde beltz kontsekutiboren artekoa.

Oraindik iturri bakarrarekin, uhin-luzera aldatu ezazu, irudia botoia klikatu eta ikusten da uhin-luzera nola aldatzen den.

Bi iturri edo gehiago aukeratzen badira, leihatilan hiru irudi adierazten dira: ezkerraldean, interferentzia patroia ikusten da, ur-kubeta batean ikusten dena bezalakoa, alegia ur-olatutxoek osatzen dituzten interferentziak. Erdiko aldean, puntu bakoitzeko intentsitatea erakusten da (uhin erresultanteak duen energiaren batezbestekoa). Intentsitate maximoa zuriz adierazten da eta minimoa beltzez. Eta eskumako aldean, intentsitatearen grafikoa adierazten da plano bertikal batean moztuta. Plano bertikala aukeratu egin daiteke, alegia, ezkerretik eskumara desplazatu daiteke, erdiko irudiko laukitxo gorria saguaz desplazatzen. Planoa lerro hori batez markatuta dago. Konpara itzazu eskumako aldeko grafikoak iturrietatik hurbil edo urrun.