Oszilazioak

Osziladoreak (II)

Osziladore
ez lineala (I)

Osziladore
ez lineala (II)

Pendulua

Oszilazio ez
harmonikoak

Molekula diatomikoa

Morse osziladorea

Zilindro errodatzaile
baten oszilazioak

Pistoi baten higidura

Atwood-en makina

Partikularen higidura

Saiakuntza

Erreferentzia

Orri honetan deskribatuko da m masadun partikula baten higidura, jasandako F(x) indarrak Morse potentzialaren itxura duenean, alegia horrelako funtzio matematikoaz:

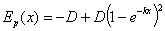
Horrelako potentzial batek minimo bat dauka x=0 posizioan eta bere balioa E_p(x₀)= -D.

• Baldin x→ ∞, orduan E_p(x) funtzioak zerora jotzen du.

• Baldin x→ -∞, orduan E_p(x) funtzioak infinitura jotzen du.

Ondorengo irudiak erakusten du E_p(x) funtzioa k eta D parametroen balio finko batzuekin: k=1, eta D=1

Partikularen higiduraren deskribapen kualitatiboa

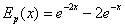
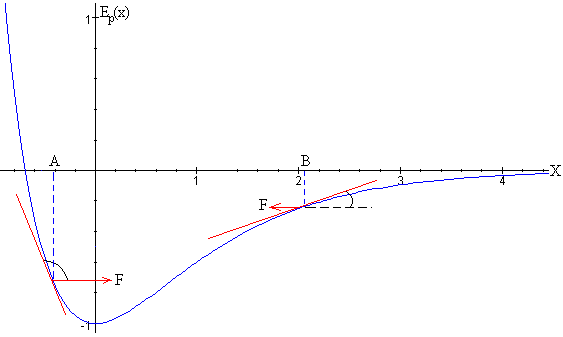
E_p(x) funtzioa ezagututa, x-ekiko deribatuak F(x) indarra ematen du, partikulak jasaten duena:

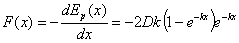
x=0 posizioan, F(x)=0, hau da, koordenatuen jatorria oreka-posizioa da, eta egonkorra, minimoa delako.

Oreka-posiziotik kanpo, partikulak jasandako indarra E_p(x) kurbaren malda da (zeinua aldatuta).

• Partikula irudiko A posizioan badago, malda negatiboa da, beraz indarra positiboa. Malda handia denez, indarra handia da.

• Partikula irudiko B posizioan baldin badago, malda positiboa da, beraz indarra negatiboa. Malda txikia denez, indarra ere bai.

Partikulak jasaten duen indarra kontserbakorra denez, E energia totalak konstante dirau:

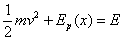
Energia potentzialaren funtzioa irudikatuz, E_p(x), eta E energía totala ezaguna bada (zuzen horizontal gorria) partikularen higidura kualitatiboki deskriba daiteke:

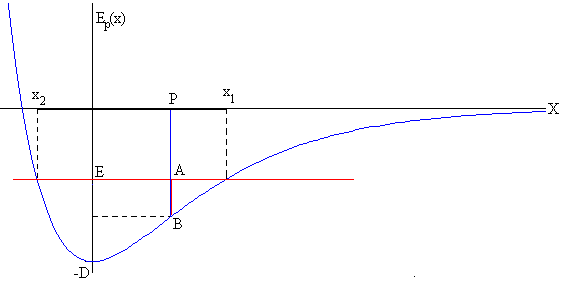
1. Partikularen E energia totala tarte honetan badago: -D<E<0, orduan partikularen higidura mugatuta dago eta oszilatu egingo du oreka egonkorreko posizioaren inguruan (x=0), x₁ eta x₂ posizioen artean, x₂ negatiboa izanik eta x₁ positiboa, irudiak erakusten duen bezala.

Posizio bi horiek kalkula daitezke E_p(x) =E ekuazioa ebatzita:

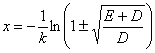
Partikula P posiziotik pasatzen den unean, bere energia totala PA zuzenkiaren luzera da (urdina) energia potentziala berriz, PB zuzenkiaren luzera, eta beraz energia zinetikoa AB zuzenkiarena (gorria).

Energia zinetikoa maximoa da partikula jatorritik pasatzen den unean, eta nulua da muturreko bi posizioetan, x₁ eta x₂.

2. Partikularen E energia totala positiboa bada, E>0, orduan partikularen higidurak muga bakar bat dauka: x_m. Oso urrutitik baldin badator, posizio horretan gelditu eta berriz ere infinituraino itzuliko da.

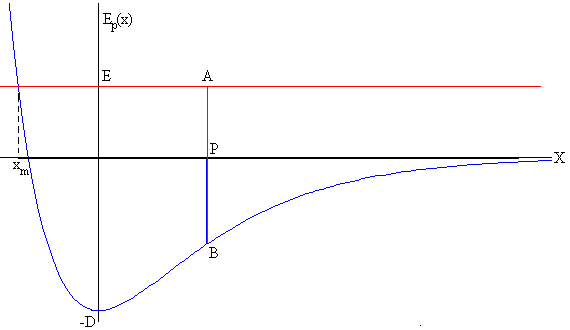
E>0 kasuan, E_p(x) =E ekuazioak soluzio bakar bat dauka:

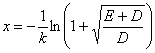
Partikula P posiziotik pasatzen den unean, bere energia totala PA zuzenkiaren luzera da, bere energia potentziala PB eta beraz energia zinetikoa AB.

Energia zinetikoa maximoa da partikula jatorritik pasatzen denean, aldiz, nulua da x_m posizioan dagoenean.

Partikularen higidura

Defini dezagun dimentsiorik gabeko parametro bat, ρ, honako baldintza hau betetzen duena: E+D=ρ·D

1. Definizio horren arabera, partikula bi aldeetatik mugatuta dago ρ<1 bada, eta honako eskualdean:

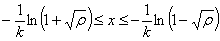
2. Partikula mutur batetik soilik mugatuta dago eta bestetik infinituraino mugi daiteke, ρ>1 bada. Hona hemen muga:

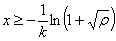
3. Baldin E=0 edo ρ=1 , orduan partikula mutur batetik soilik mugatuta dago eta bestetik infinituraino mugi daiteke, ρ>1 bezala baina:

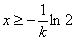
Kalkula dezagun partikularen x posizioa t denboraren menpe kasu guztietan, lehen ordenako ekuazio diferentzial bat integratuz. Lehenik idatz dezagun energiaren kontserbazio-teorema ekuazio diferentzial gisa:

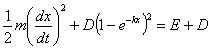
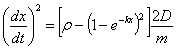
1. Lehenik ρ<1 kasua

Aldagai aldaketa egin dezagun:

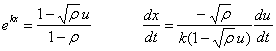
Lehen ordenako ekuazio diferentziala aldatu egiten da eta, zenbait buruketa egin ondoren, honela idatz daiteke, modu errazagoan integratzeko:

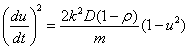
arccos u=γt-γt₀
u=cos(γt-γt₀)

γt₀ integrazio-konstante bat da, eta hasierako baldintzetatik determinatzen da: partikularen x₀  posizioa t=0 aldiunean.

Aldagai aldaketa deseginda:

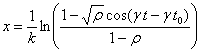
Ondoko programa interaktiboan partikularen hasierako posizioa (t=0) jatorria bera da x=0, orduan t₀  aldiuneak honakoa balio du:

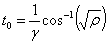
2. Ondoren ρ>1 kasua

Egin dezagun aldagai aldaketa:

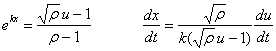
Lehen ordenako ekuazio diferentziala aldatu egiten da eta, zenbait buruketa egin ondoren, honela idatz daiteke, modu errazagoan integratzeko:

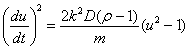
arccosh u=γt-γt₀
u=cosh(γt-γt₀)

γt₀  integrazio-konstante bat da, eta hasierako baldintzetatik determinatzen da: partikularen x₀  posizioa t=0 aldiunean.

Aldagai aldaketa deseginda:

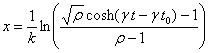
Ondoko programa interaktiboan partikularen hasierako posizioa (t=0) jatorria bera da x=0, orduan t₀  aldiuneak honakoa balio du:

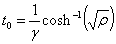
3. Azkenik, ρ=1 kasua

Egin dezagun aldagai aldaketa:

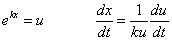
Lehen ordenako ekuazio diferentziala aldatu egiten da eta, zenbait buruketa egin ondoren, honela idatz daiteke, modu errazagoan integratzeko:

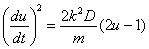
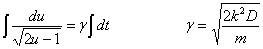
2u-1=(γt-γt₀)²

γt₀  integrazio-konstante bat da, eta hasierako baldintzetatik determinatzen da: partikularen x₀  posizioa t=0 aldiunean.

Aldagai aldaketa deseginda:

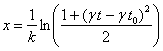
Ondoko programa interaktiboan partikularen hasierako posizioa (t=0) jatorria bera da x=0, orduan t₀  aldiuneak honakoa balio du:

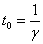
Adibidea:

• Demagun k=1

• Eta D=1

1. Partikularen energía totala, E= -0.5

Energia-parametroa: ρ=(E+D)/D=0.5<1

Orduan partikulak muturreko posizio biren artean oszilatuko du:

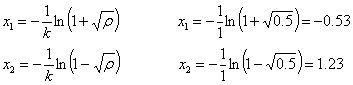
Hona hemen higiduraren ekuazioa:

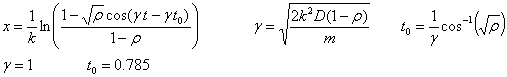
Esaterako, t=2.0 aldiunean, partikularen posizioa hau da: x=0.41.

Bere energia potentziala:

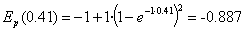
Energia zinetikoa: E_k= E-E_p= 0.387

Beraz, partikularen abiadura:

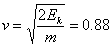
2. Partikularen energía totala, E=0.5

Energia-parametroa: ρ=(E+D)/D=1.5>1

Partikula jatorritik abiatzen da eta honako posizioraino iristen da:

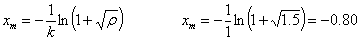
Higiduraren ekuazioa:

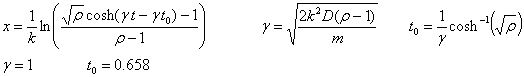
Esaterako,  t=2.0 aldiunean, partikularen posizioa hau da: x=1.10

Bere energia potentziala:

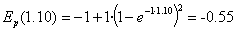
Energia zinetikoa: E_k=E-E_p=1.05

Beraz, partikularen abiadura: v=1.45

3. Partikularen energía totala, E=0

Energia-parametroa: ρ=(E+D)/D=1

Partikula jatorritik abiatzen da eta honako posizioraino iristen da:

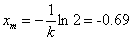
Higiduraren ekuazioa:

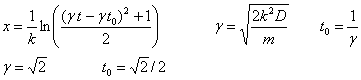
Esaterako,  t=2.0 aldiunean, partikularen posizioa hau da: x=0.77

Bere energia potentziala:

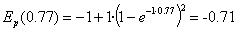
Energia zinetikoa:  E_k=E-E_p=0.71

Beraz, partikularen abiadura, v=1.19

Saiakuntza

Aukeran idatz daitezke:

• E_p(x) energia potentzialaren k konstantea, desplazamendu-barrari saguaz eragiten.

• Partikularen E energia totala, desplazamendu-barrari saguaz eragiten.

• D parametroa finkotzat hartu da, D=1

Hasi botoia sakatu.

Partikularen E energia totala negatiboa bada (-1<E<0 tartean), partikulak oszilatu egiten du bi muturren artean: x₁ eta x₂.

Aldiz, E energia totala positiboa edo nulua bada, partikula jatorritik ezkerrera mugitzen hasten da, muturreko x_m posizioraino iritsi eta berriro eskumarantz abiatzen da, infinituraino.

Energiaren grafikoan, zuzenki bertikalean zati urdinak energia potentziala adierazten du, zati gorriak energia zinetikoa eta bektoreak F(x) indarra, partikulari eragiten ari zaiona.

Leihatilaren goiko aldean, zenbakiz adierazten dira uneoro idatzita, t denbora, x posizioa, v abiadura, E_p energia potentziala, eta E_k energia zinetikoa.