Electromagnetismo |
Autoinducción e Inducción mutua Autoinducción. Circuito R-L Circuitos acoplados (I) Circuitos acoplados (II) Oscilaciones eléctricas Circuito LCR conectado a una batería
Elementos de un circuito de C.A. Sistema electro- mecánico oscilante Medida de la auto- inducción de un anillo Circuito LCR en serie Resonancia Medida de la velocidad de la luz en el vacío Efectos mecánicos de la ley de Faraday Caída de un imán El anillo de Thomson (I) El anillo de Thomson (II) |
Circuito formado por dos
condensadores, una resistencia y una autoinducción Soluciones de la ecuación diferencial Carga final de los condensadores |
|||
|
En la página “Agrupación de condensadores” hemos estudiado el problema de dos condensadores iguales de capacidad C que se conectan en paralelo. Cuando se carga un condensador con carga Q y se conecta a otro descargado, en el estado final, ambos condensadores se cargan con la misma carga Q/2. La energía eléctrica acumulada en los condensadores en el estado final es justamente la mitad que la energía inicial. Para explicar esta pérdida de energía se ha supuesto que los entre los dos condensadores hay una resistencia R. La diferencia de energía se disipa en la resistencia en forma de calor. Aunque este modelo parece satisfactorio ya que es natural incluir la resistencia R de los cables que conectan los condensadores, permanece un problema sin resolver. La corriente i cambia desde un valor i=0, para t<0 a un valor i0=Q/(RC) para t=0. La razón de esta discontinuidad es que no hemos incluido la autoinducción L que tiene cualquier circuito
Circuito formado por dos condensadores, una resistencia y una autoinducciónConsideremos el siguiente circuito formado por dos condensadores de capacidades C1 y C2, una resistencia R y una autoinducción L.
El condensador de capacidad C1 está cargado con una carga Q, y el condensador de capacidad C2 está inicialmente descargado. En el instante t=0, se cierra el circuito. El condensador de capacidad C1 se descarga y carga al condensador de capacidad C2. En un instante dado t, tendremos que
Medimos las diferencias de potencial entre los puntos a y b, b y c, c y d, d y a. En un circuito cerrado se cumple Vab+Vbc+Vcd+ Vda =0
La ecuación del circuito es
Con q1+q2=Q. Si inicialmente el condensador C2 está descargado q2=0, la carga q1 disminuye con el tiempo y la carga q2 aumenta con el tiempo, la intensidad i (carga por unidad de tiempo) valdrá
La ecuación del circuito se escribe en términos de q2
o bien,
La solución de esta ecuación diferencial es de la forma
La constante y1 es la solución particular y la segunda, la solución general que ya encontramos en el estudio de las oscilaciones amortiguadas. Introduciendo la solución particular y1 en la ecuación diferencial tenemos que y1=QC2/(C1+C2) Las condiciones iniciales q2=0, y dq2/dt=0 determinan los valores de A y B.
Comprobamos que en el instante t=0, q2=0 e i=0. Después de un tiempo muy grande, t→∞, i→0 y
Deducción alternativaDerivamos la ecuación del circuito respecto del tiempo
Quedando la ecuación diferencial de las oscilaciones amortiguadas
Para integrar la ecuación diferencial necesitamos conocer la intensidad i en el instante t=0, y el valor de la derivada primera di/dt de la intensidad en dicho instante. Las condiciones iniciales son por tanto, en el instante t=0, la intensidad i=0. El condensador de capacidad C2 se encuentra descargado q2=0, el condensador de capacidad C1 tiene una carga inicial q1=Q. La ecuación del circuito se escribe para t=0
Soluciones de la ecuación diferencialLa solución de la ecuación diferencial es la siguiente: Oscilaciones amortiguadas (g<w0) |
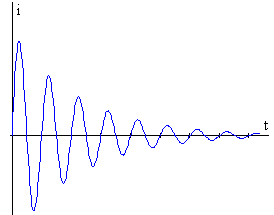 |
Para obtener esta imagen, en el applet de las oscilaciones amortiguadas, se introduce en los controles de edición:
|
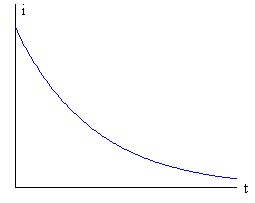 |
Esta solución, se puede comparar con la que obtuvimos sin tener en cuenta la autoinducción del circuito
que afirma que la intensidad i disminuye exponencialmente con el tiempo. |
Se introduce
La capacidad C1 del primer condensador en μF, inicialmente cargado, en el control de edición titulado Capacidad 1.
La capacidad C2 del segundo condensador en μF, inicialmente descargado, en el control de edición titulado Capacidad 2.
La resistencia R, en mΩ, en el control de edición titulado Resistencia
La autoinducción L de la bobina, en μH, en el control de edición titulado Autoinducción
Se puede modificar la escala de los tiempos del eje horizontal de la representación gráfica, eligiendo un número o una fracción en el control de selección titulado Escala.
Se pulsa el botón titulado Empieza
Se observa como la carga fluye de un condensador al otro, de forma análoga a como la carga fluye entre los vasos comunicantes. El flujo de cargas (la intensidad de la corriente) está representado por el movimiento de puntos de color rojo.
Si la resistencia R no es nula, la carga en cada uno de los condensadores tiende hacia un valor límite.
En la gráfica se representa, en el eje vertical la carga q1/Q y q2/Q y en el eje horizontal el tiempo t, medido en μs.
Ejemplo:
Se introduce
Capacidades: C1=3·10-6 F, C2=2·10-6 F
Resistencia R=50·10-3 Ω
Autoinducción L=2·10-6 H
Calculamos
La constante de amortiguamiento γ=12500 s-1
La frecuencia angular natural ω0=645497 rad/s
La frecuencia de la oscilación amortiguada ω=645377 rad/s
Ambas frecuencias son prácticamente iguales
En el instante t=100·10-6 s calculamos la carga
![]()
en el condensador de capacidad C2, obtenemos q2/Q=0.41
en el condensador de capacidad C1, q1/Q=1-q2/Q=0.59
Siendo Q, la carga inicial en el instante t=0.
Después de un tiempo muy grande las cargas en cada uno de los condensadores tiende hacia
q2/Q=0.4
q1/Q=0.6
Powell R. A. Two-capacitor problem: A more realistic view. Am. J. Phys. 47 (5) May 1979, pp. 460-462