| En esta página se describe un experimento para medir el índice adiabático
del aire por el procedimiento de Clément y Désormes. En esta experiencia
simulada se aplicará la:
- Ecuación de estado de un gas ideal: PV=nRT
- Transformación
adiabática: PVg =cte.
- Ecuación
fundamental de la estática de fluidos: p=p0+r
gh
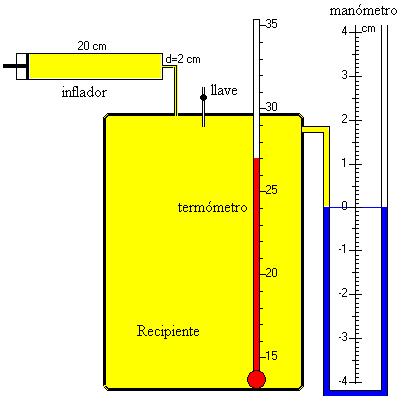
El dispositivo experimental consta de un recipiente cuyo volumen es V1
que contiene aire, está conectado a un manómetro necesario para medir pequeñas
diferencias de presión y está cerrado por una llave que comunica con la atmósfera.
- Accionando un inflador (bomba de una bicicleta) añadimos aire al recipiente y
aumentamos su presión al no cambiar el volumen. De modo que, el estado inicial del aire
contenido en el recipiente es el siguiente:
- Temperatura ambiente T1
- Presión p1 algo superior a la presión atmosférica p0.
- n1
moles de aire contenidos en el volumen V1 del
recipiente.
- Se abre la llave que comunica el recipiente con la atmósfera, el aire experimenta una
transformación adiabática, disminuyendo rápidamente su presión,
hasta alcanzar la presión atmosférica p0.
- Temperatura T2
- Presión p0
- n2 moles de aire en el volumen fijo V1 del recipiente.
O bien, n1 moles en el volumen mayor (expansión) V2=V1·n1/n2.
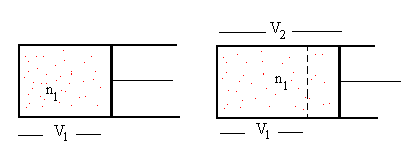
Como vemos en la figura, n1 moles de un gas se expanden
desde un volumen V1 hasta ocupar un volumen V2, el
número de moles n2 que permanece en el volumen V1
después de la expansión será n2=n1·V1/V2
- Se cierra la llave y se espera cierto tiempo a que el aire del recipiente vuelva a
adquirir la temperatura ambiente (calentamiento a volumen constante). El estado final
será
- Temperatura T1
- Presión p2
- n2 moles de aire en el volumen V1 del recipiente, o n1
moles en el volumen V2.
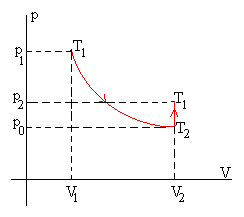 |
El proceso 1-2 es adiabático, por tanto,
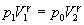
Como el estado inicial 1 y el estado final 3 tienen la misma temperatura, se cumple
p1V1=p2V2 |
Eliminando la cantidades desconocidas V1 y V2 de
este sistema de dos ecuaciones, tenemos.
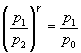
Despejando el índice adiabático g
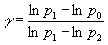
Las presiones p1 y p2 las podemos poner como suma
de la presión atmosférica más lo que nos marca el manómetro. Si r es la densidad del líquido manométrico, de la ecuación
fundamental de la estática de fluidos tenemos.
p1=p0+r gh1
p2=p0+r gh2
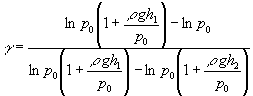
como presiones manométricas r gh son
muy pequeñas comparadas con la presión atmosférica p0 podemos hacer
la siguiente aproximación ln(1+x)» x
Llegamos finalmente, una expresión muy simplificada.
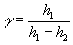
Ejemplo
Los datos necesarios para realizar los cálculos son los siguientes
- Dimensiones del inflador: cilindro de longitud 20 cm y 1 cm de radio
- Volumen del recipiente: 10 litros ó 0.01 m3
- Temperatura ambiente 27ºC ó 300 K
- Presión atmosférica: 101300 Pa
- Líquido manométrico: mercurio de densidad 13550 kg/m3.
- Constante R de los gases 0.082 atm·l/(K mol) ó 8.314 J/(K mol)
- Índice adiabático del aire 1.4
- Número de moles n1 iniciales en el recipiente a la
temperatura ambiente.
1·10=n0·0.082·300 por tanto, n0=0.41 moles
Se acciona N veces el inflador, por lo que se incrementa en Dn,
el número de moles del recipiente.
1·N·2·p ·(0.1)2=Dn·0.082·300
Por ejemplo si N es 8 veces tenemos que Dn=0.02
moles
El número de moles de aire en el recipiente será n1=n0+Dn
n1=0.43 moles
La presión del recipiente será
p1V1=n1RT
p1·10=0.43·0.082·300 por tanto, p1=1.05 atm
La presión se ha incrementado en 0.05 atm, lo que equivale a una altura de la columna
de mercurio
0.05·101300=13550·9.8·h1 por tanto, h1=0.038 m
ó 2·1.9 cm
el desnivel entre las dos ramas es de 3.8 cm
- Expansión adiabática
Se abre la llave y el recipiente pierde n1-n2 moles de
aire, donde n1 el número de moles iniciales y n2 los
moles de aire finales cuando alcanza la presión atmosférica.
El aire se expande adiabáticamente desde una presión p1 y un
volumen V1=10 litros hasta que alcanza la presión atmosférica.
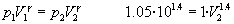
El volumen V2 es 10.35 litros
Si en el volumen V2 hay n1 moles en el volumen V1
del recipiente habrán quedado n2 moles, tal que n2=n1·V1/V2.
n2=0.412 moles, se han escapado n1-n2=0.01
moles de aire al abrir la llave
La temperatura final del recipiente cuando se ha alcanzado la presión atmosférica
1·10=n2·0.082·T2
T2=296 ºK ó 23 ºC, más baja que la temperatura ambiente que es
de 27º C ó 300 ºK
- El aire del recipiente se calienta hasta alcanzar la temperatura ambiente,
aumentando la presión
p3·10=n2·0.082·300
p3=1.01 atm, es decir, la presión se ha incrementado en 0.01 atm, lo
que equivale a una altura de la columna de mercurio de
0.01·101300=13550·9.8·h2 por tanto, h2=0.011 m
ó 2·0.55 cm
es decir el desnivel entre las dos ramas del manómetro es de 1.1 cm
Pulsamos el botón titulado Nuevo. A continuación, se pulsa varias veces el
botón titulado Llenar de aire. Cada vez que se pulsa este botón el émbolo del
inflador se desplaza y llena el recipiente de aire. Observamos en el manómetro como se va
elevando la presión del recipiente.
Después de haber accionado de 5 a 10 veces el inflador, se abre la llave pulsando en
el botón titulado Abrir llave, apuntamos el desnivel h1 entre
las dos ramas del manómetro. El aire sale por la parte superior del recipiente, y la
presión disminuye rápidamente, la temperatura baja unos grados.
Cuando la presión toma el valor inicial, es decir, el manómetro marca cero, se cierra
la llave pulsando el mismo botón que ahora se titula Cierra llave. La temperatura
asciende al calentarse el aire del recipiente. La presión asciende como observamos en el
manómetro hasta marcar un desnivel entre sus ramas de h2.
Ejemplo
Se ha accionado 8 veces el inflador. El desnivel entre las dos ramas del manómetro es
de h1=2·1.9 cm
Se abre la llave hasta que la presión en el recipiente vuelve a ser la atmosférica,
el manómetro marca cero. Después se cierra la llave, esperamos un poco de tiempo hasta
que se caliente el aire del recipiente y medimos el desnivel entre las dos ramas del
manómetro h2=2·0.5.
Aplicamos la fórmula
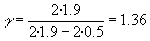
El valor del índice adiabático del aire es 1.4 |