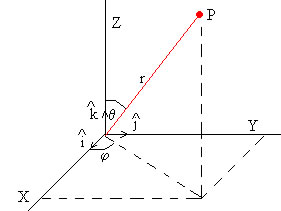
Un Sistema de Referencia está formado por un punto O denominado origen y una base formada por tres vectores unitarios $\widehat{i},\widehat{j},\widehat{k}$ mutuamente perpendiculares. Las direcciones de dichos vectores son los ejes X, Y y Z, respectivamente.

El vector posición del punto P, se expresa $\overrightarrow{r}=x\widehat{i}+y\widehat{j}+z\widehat{k}$ , o bien, en términos de los ángulos θ y φ

x=r·sinθ·cosφ
y=r·sinθ·sinφ
z=r·cosθ

${\displaystyle \overrightarrow{r}=r\sin \theta \cos \phi \widehat{i}+r\sin \theta \sin \phi \widehat{j}+r\cos \theta \widehat{k}}$

Sistema de Referencia en el centro de la Tierra

Situamos el observador en el centro de la Tierra que observa como el Sol se mueve en una órbita inclinada ε=23.45° respecto del plano ecuatorial.

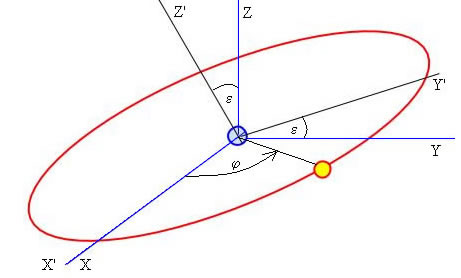
En el Sistema de Referencia de la eclíptica la posición del Sol se define con respecto a los ejes X', Y' Z'. La posición angular del Sol está determinada por el ángulo φ que varía de 0° en el equinocio de primavera (en Marzo) hasta completar 360° un año después. El eje X=X' tiene la dirección de la línea de los equinocios

El vector unitario $\widehat{S}$ que apunta desde el centro de la Tierra hacia el Sol se expresa en este SR (Sistema de Referencia)

${\displaystyle \widehat{S}=\cos \phi ·\widehat{i}\text{'}+\sin \phi ·\widehat{j}\text{'}}$

Donde $\widehat{i}\text{'},\widehat{j}\text{'}$ son vectores unitarios en las direcciones X' y Y' respectivamente.

Sistema de Referencia girado un ángulo ε

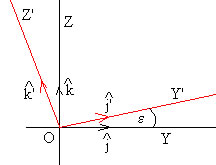
Vamos a expresar el vector $\widehat{S}$ en el SR X,Y,Z, donde el plano XY coincide con el plano del Ecuador. El SR Ecuatorial está relacionado con el SR de la Eclíptica por una rotación de ángulo ε alrededor del eje X=X'. Debido a que el eje de la Tierra forma un ángulo de ε=23.45° con la perpendicular al plano de la eclíptica, la relación entre los vectores unitarios puede verse en la figura.

${\displaystyle \begin{array}{l}\widehat{i}\text{'}=\widehat{i}\\ \widehat{j}\text{'}=\cos \epsilon ·\widehat{j}+\sin \epsilon ·\widehat{k}\\ \widehat{k}\text{'}=-\sin \epsilon ·\widehat{j}+\cos \epsilon ·\widehat{k}\end{array}}$

El vector $\widehat{S}$ se expresa en el SR Ecuatorial X,Y,Z del siguiente modo

${\displaystyle \widehat{S}=\cos \phi ·\widehat{i}+\sin \phi \cos \epsilon ·\widehat{j}+\sin \phi \sin \epsilon ·\widehat{k}}$

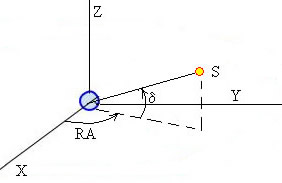
En el SR Ecuatorial X,Y,Z la posición del Sol se puede escribir utilizando dos ángulos: el ángulo de declinación δ y el ángulo RA, tal como vemos en la figura.

${\displaystyle \widehat{S}=\cos \delta \cos RA·\widehat{i}+\cos \delta \sin RA·\widehat{j}+\sin \delta ·\widehat{k}}$

Es también útil considerar un nuevo Sistema de Referencia X" Y" Z" en el cual X" e Y" están en el plano ecuatorial X Y y el eje Z" coincide con Z, el eje de la Tierra. En este SR, el vector $\widehat{S}$ que apunta al Sol siempre está en el plano X" Z"

Sistema de Referencia Local

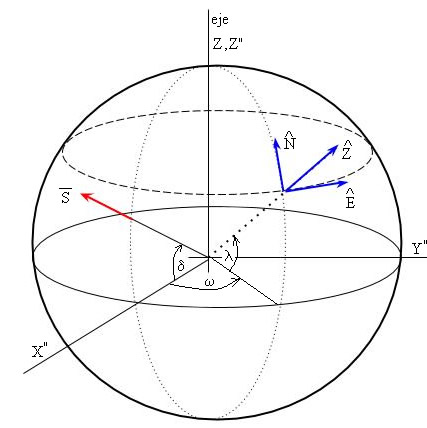
Consideramos ahora un punto situado sobre la superficie de la Tierra cuya latitud λ y cuyo ángulo horario ω. El Sistema de Referencia Local está formado por un origen situado en el punto y una base definida por tes vectores unitarios $\widehat{E},\widehat{N},\widehat{Z}$ mutuamente perpendiculares. Las direcciones de dichos vectores son, la dirección Oeste-Este (tangente al paralelo en el punto), la dirección Sur-Norte (tangente al meridiano en el punto), y la dirección radial.

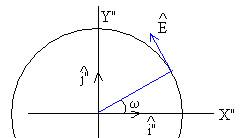
Expresamos los vectores unitarios $\widehat{E},\widehat{N},\widehat{Z}$ , en términos de los vectores unitarios $\widehat{i}",\widehat{j}",\widehat{k}"$

Como vemos en la figura, $\widehat{E}=-\sin \omega ·\widehat{i}"+\cos \omega ·\widehat{j}"$

Al principio de esta página ya vimos cómo se expresaba el vector $\overrightarrow{r}$ en coordenadas esféricas

${\displaystyle \widehat{Z}=\cos \lambda \cos \omega ·\widehat{i}"+\cos \lambda \sin \omega ·\widehat{j}"+\sin \lambda ·\widehat{k}"}$

Calculamos el vector $\widehat{N}$ a partir de $\widehat{Z}$ y $\widehat{E}$, fijándonos que el producto vectorial $\widehat{N}=\widehat{Z}\times \widehat{E}$ , del mismo modo que se cumple que $\widehat{k}=\widehat{i}\times \widehat{j}$

${\displaystyle \begin{array}{l}\widehat{N}=\widehat{Z}\times \widehat{E}=\left|\begin{array}{ccc}\widehat{i}"& \widehat{j}"& \widehat{k}"\\ \cos \lambda \cos \omega & \cos \lambda \sin \omega & \sin \lambda \\ -\sin \omega & \cos \omega & 0\end{array}\right|=\hfill \\ -\cos \omega \sin \lambda ·\widehat{i}"-\sin \omega \cos \lambda ·\widehat{j}"+\cos \lambda ·\widehat{k}"\hfill \end{array}}$

El vector $\widehat{S}$ está en el plano X" Z", y forma un ángulo δ (declinación) con el eje X"

${\displaystyle \widehat{S}=\cos \delta ·\widehat{i}"+\sin \delta ·\widehat{k}"}$

Altitud y Acimut

Expresamos el vector $\widehat{S}$ en el SR Local, para ello, calculamos las componentes del vector $\widehat{S}$ a lo largo de las direcciones de los vectores unitarios $\widehat{E},\widehat{N},\widehat{Z}$ mediante el producto escalar (Recordar que la componente X" del vector $\widehat{S}$ es el producto escalar $S_x=\widehat{S}·\widehat{i}"$ )

${\displaystyle \begin{array}{l}\widehat{N}=-\cos \omega \sin \lambda ·\widehat{i}"-\sin \omega \cos \lambda ·\widehat{j}"+\cos \lambda ·\widehat{k}"\hfill \\ \widehat{E}=-\sin \omega ·\widehat{i}"+\cos \omega ·\widehat{j}"\hfill \\ \widehat{Z}=\cos \omega \cos \lambda ·\widehat{i}"+\sin \omega \cos \lambda ·\widehat{j}"+\sin \lambda ·\widehat{k}"\hfill \\ \overrightarrow{S}=\cos \delta ·\widehat{i}"+\sin \delta ·\widehat{k}"\hfill \\ S_N=\overrightarrow{S}·\widehat{N}=-\cos \omega \sin \lambda \cos \delta +\cos \lambda \sin \delta \hfill \\ S_E=\overrightarrow{S}·\widehat{E}=-\sin \omega \cos \delta \hfill \\ S_Z=\overrightarrow{S}·\widehat{Z}=\cos \omega \cos \lambda \cos \delta +\sin \lambda \sin \delta \hfill \\ \overrightarrow{S}=-\sin \omega \cos \delta ·\widehat{E}+(\cos \lambda \sin \delta -\cos \omega \sin \lambda \cos \delta )·\widehat{N}+\hfill \\ (\cos \omega \cos \lambda \cos \delta +\sin \lambda \sin \delta )·\widehat{Z}\hfill \end{array}}$

El vector $\widehat{S}$ se puede expresar como vemos en la figura en términos de dos ángulos α_s (altitud del Sol) y γ_s (acimut del Sol)

${\displaystyle \widehat{S}=\cos {\alpha }_s\sin {\gamma }_s·\widehat{E}+\cos {\alpha }_s\cos {\gamma }_s·\widehat{N}+\sin {\alpha }_s·\widehat{Z}}$

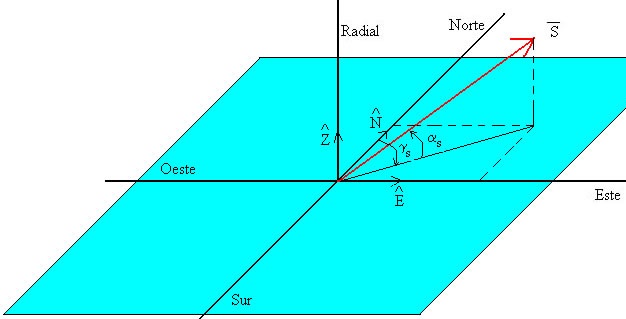
Igualando las componentes, obtenemos tres relaciones:

cosα_s·sinγ_s=-sinω·cosδ
cosα_s·cosγ_s=cosλ·sinδ-sinλ·cosω·cosδ
sinα_s=cosλ·cosω·cosδ+sinλ·sinδ

De las cuales, solamente precisamos dos:

1. Obtenemos α_s la altitud del Sol

sinα_s=cosλ·cosω·cosδ+sinλ·sinδ

2. Obtenemos γ_s el acimut del Sol medido desde el Norte (positivo en el sentido de las agujas del reloj, hacia el Este)

${\displaystyle \cos {\gamma }_s=\frac{\cos \lambda \sin \delta -\cos \omega \sin \lambda \cos \delta }{\cos {\alpha }_s}}$

Para calcular γ_sse precisa calcular el arco coseno que devuelve un ángulo entre 0-180°. Pero el acimut del Sol puede tomar un valor en el intervalo 0-360°. Mediante la siguiente regla obtenemos el ángulo adecuado:

Calculamos γ_c que está en el intervalo 0≤γ_c≤180° mediante

${\displaystyle {\gamma }_c=\arccos \left(\frac{\cos \lambda \sin \delta -\cos \omega \sin \lambda \cos \delta }{\cos {\alpha }_s}\right)}$

• Si el ángulo horario ω<0 entonces γ_s= γ_c
• Si el ángulo horario ω>0 entonces γ_s= 360-γ_c

Como vemos en la figura:

• si 0≤γ_s≤180° entonces el Sol está al Este del observador y esto se corresponde con las horas entre medianoche y mediodía en las que ω<0
• si 180≤γ_s≤360° entonces el Sol está al Oeste del observador y esto se corresponde con las horas entre mediodía y medianoche en las que ω>0

Altura máxima

A mediodía, el ángulo horario ω=0, el Sol está exactamente en el meridiano local, apuntando hacia el Sur, por lo que el acimut γ_s=180° y el Sol tiene la máxima altitud α_sm.

sinα_sm=cosλ·cosδ+sinλ·sinδ

por lo que α_sm=90-(λ-δ)=90-λ+δ

• La mayor altitud α_sm ocurre en el solsticio de verano cuando δ=23.45°. En Bilbao λ=43.3°. La máxima altidud al mediodía el día 21 de junio es α_sm=90-43.3+23.45=70.15°
• La menor altitud α_sm ocurre en el solsticio de invierno cuando δ=-23.45°. En Bilbao λ=43.3°. La mínima altitud al mediodía el día 21 de diciembre es α_sm=90-43.3-23.45=23.25°

Amanecer y Anochecer (Orto y Ocaso)

Cuando la altitud α_s=0 se dice que amanece o se pone el Sol.

${\displaystyle \begin{array}{l}\cos \omega =-\frac{\sin \lambda \sin \delta }{\cos \lambda \cos \delta }=-\tan \lambda ·\tan \delta \\ \Delta h=\frac{1}{15}\arccos \left(-\tan \lambda ·\tan \delta \right)\end{array}}$

El arco coseno devuelve el ángulo en grados y 15 grados equivale a una hora. El ángulo horario ω=0 al mediodía. El ángulo horario al amanecer es negativo ω<0 y al anochecer es positivo ω>0. Luego la hora del Orto h_sr=-Δh y la hora del Ocaso es h_ss=Δh. La duración del día es 2·Δh

Vamos a determinar la hora local del Orto y Ocaso en Bilbao el día 21 de junio de 2013 (N=172 es el número de día). Bilbao tiene una latitud de λ=43.3° y en el día del solsticio de verano δ=23.45°, por lo que Δh=7.61h

La hora del Orto es -7.61h antes y la del Ocaso +7.61h después medidas desde el mediodía. La duración del día es de 15h 13min

En verano la hora de Bilbao es UTC+2, por lo que el mediodía se produce a las 14h hora local, a la que hemos de añadir la corrección debida a la ecuación del tiempo Δt y a la longitud de -2.94° hacia el Oeste (cuatro minutos por grado ó una hora cada 15 grados). Fijarse que amanece y anochece antes en Gerona (extremo Este) que en La Coruña (extremo Oeste), por tanto hemos de sumar los minutos correspondientes a la longitud.

La ecuación del tiempo para N=172 y h=12, es Δt=-1.39 minutos

La corrección es eqTime-4·longitude=-1.39-4·(-2.94)=10.37 minutos

El resultado es que

• amanece a las (14-7.61)·60+10.37=6h 34min
• anochece a las (14+7.61)·60+10.37=21h 47min

Las tablas de la la web del Ministerio de Fomento, nos proporcionan los siguientes datos para el día 21 de junio: 6h 32min y 21h 55min, respectivamente.

En invierno la hora de Bilbao es UTC+1 por lo que el mediodía se produce a las 13h local, a la que hemos de añadir la corrección debida a la ecuación del tiempo Δt y a la longitud de -2.94° hacia el Oeste. El 21 de diciembre el ángulo de declinación δ=-23.45° y se denomina solsticio de invierno por lo que Δh=4.39h.

La hora del Orto es -4.39h antes y la del Ocaso +4.39h después medidas desde el mediodía. La duración del día es de 8h 47min

La ecuación del tiempo para N=355 y h=12, es Δt=2.79 minutos

La corrección es eqTime-4·longitude=2.79-4·(-2.94)=14.55 minutos

El resultado es que

• amanece a las (13-4.39)·60+14.55=8h 51min
• anochece a las (13+4.39)·60+14.55=17h 38min

Las tablas de la la web del Ministerio de Fomento, nos proporcionan los siguientes datos para el día 21 de diciembre: 8h 41min y 17h 39min, respectivamente.

Creamos un script para dibujar el acimut y la altitud del Sol a cada hora, entre el orto y el ocaso. En el script se realizan las siguientes tareas:

1. Introduce mediante el comando input

• La latitud λ del lugar en grados
• La fecha (día y mes), en forma de número de día N a lo largo del año

2. Calcula la declinación δ mediante las fórmula (tómese h=12)

δ=0.006918-0.399912·cos(x)+0.070257·sin(x)-0.006758·cos(2x)+0.000907·sin(2x)-0.002697·cos(3x)
+0.001480·sin(3x).

${\displaystyle x=\frac{2\pi }{365}\left(N-1+\frac{h-12}{24}\right)}$

3. Define la función anónima que calcula la altitud del Sol α_s mediante la fórmula

α_s=arcsin(cosλ·cosω·cosδ+sinλ·sinδ)

4. Define la función anónima que calcula el azimut del Sol 0≤γ_c≤180° mediante la fórmula

${\displaystyle {\gamma }_c=\arccos \left(\frac{\cos \lambda \sin \delta -\cos \omega \sin \lambda \cos \delta }{\cos {\alpha }_s}\right)}$

5. Calcula el ángulo horario del Orto o del Ocaso tomando el medidodía como cero.

Δh=arccos(-tanλ·tan δ)

Para convertir el ángulo en horas se tiene en cuenta que 15° equivalen a 1 hora. Se multiplica el ángulo en radianes por el factor de conversión 12/π.

6. Se crea un vector w de ángulos correspondientes a las horas que van desde el valor entero de -12·Δh/π (Orto) al valor entero de 12·Δh/π (Ocaso)

Para Bilbao que tiene una latitud de λ=43.3°, el día 21 de junio, N=172, la salida del Sol se produce a las -7.61.

Creamos un vector horas con el operador : cuyos elementos son [-7 -6 -5....0 ...5 6 7]. y convertimos el vector horas en un vector w de ángulos horarios dividiendo por el factor 12/π.

Se calcula la altitud del Sol α_s para cada uno de los valores de dicho vector

Se calcula el acimut γ_s teniendo en cuenta que:

• Si el ángulo horario ω<0 entonces γ_s= γ_c
• Si el ángulo horario ω>0 entonces γ_s= 360-γ_c

En la gráfica hemos representado el ángulo suplementario de γ_s, 180-γ_s, de modo que -180≤γ_s≤180°

7. Proporciona los datos de

• La duración del día: 2·12·Δh/π
• La máxima altitud del Sol α_sm=90-λ+δ
• El ángulo de declinación, δ

lambda=input('Latitud: ');
lambda=lambda*pi/180;
N=input('Número de día: ');
h=12;
%declinación
x=2*pi*(N-1-(h-12)/24)/365;
delta=0.006918-0.399912*cos(x)+0.070257*sin(x)-0.006758*cos(2*x)
+0.000907*sin(2*x)-0.002697*cos(3*x)+0.001480*sin(3*x);

%ángulo en radianes del orto u ocaso
hr=acos(-tan(lambda)*tan(delta)); 
%altidud
alfa_s=@(w) asin(cos(lambda)*cos(w)*cos(delta)+sin(lambda)*sin(delta));
%acimut
gamma_c=@(w) acos((cos(lambda)*sin(delta)-cos(w)*sin(lambda)*cos(delta))
./cos(alfa_s(w)) );
hold on
hMax=floor(hr*12/pi); %hora del orto u ocaso, sin decimales

%desde el orto al mediodía
h=-hMax:0;
w=h*pi/12; %convierte hora en radianes
a_s=alfa_s(w)*180/pi;
g_c=180-gamma_c(w)*180/pi;
plot(g_c,a_s,'-ro','markersize',4, 'markerfacecolor','y');

%desde el mediodía al ocaso
h=0:hMax;
w=h*pi/12;
a_s=alfa_s(w)*180/pi;
g_c=180-(2*pi-gamma_c(w))*180/pi;
plot(g_c,a_s,'-ro','markersize',4, 'markerfacecolor','y');
axis([-150 150 0 90]);

%muestra datos 
str=sprintf('duración día: %1.3fh',2*hr*12/pi);
text(-150,87,str)
str=sprintf('altitud máxima: %1.3f°',90-(lambda-delta)*180/pi);
text(-150,82,str)
str=sprintf('declinación: %1.3f°',delta*180/pi);
text(-150,78,str)
grid on
hold off

Corremos el script en la ventana de comandos

>> orto_ocaso
Latitud: 43.3
Número de día: 172

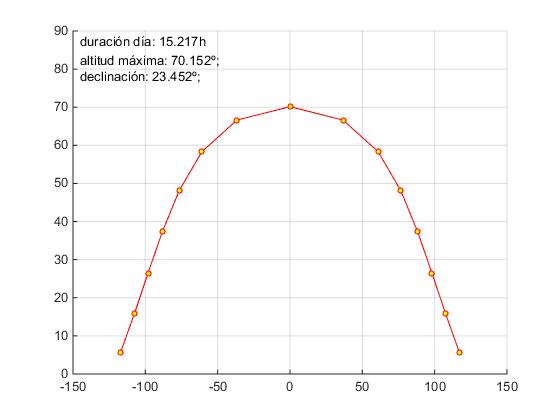
A partir del script orto-ocaso_1 creamos el script orto-ocaso que es una representación tridimensional de la trayectoria del Sol empleando la función plot3. Conocidos la altitud del Sol α_s y el acimut γ_s para cada una de las horas. Calculamos el vector unitario de componentes (x,y,z) que señala la orientación del Sol en la esfera celeste.

${\displaystyle \widehat{S}=\cos {\alpha }_s\sin {\gamma }_s·\widehat{E}+\cos {\alpha }_s\cos {\gamma }_s·\widehat{N}+\sin {\alpha }_s·\widehat{Z}}$

x=cosα_s·sinγ_s
y=cosα_s·cosγ_s
z=sinα_s

Para ver un dibujo tridimensional desde distintos puntos de vista, se actúa sobre el botón en la barra del menú titulado Rotate 3D. Se va cambiando el valor de los parámetros del comando view tal como puede apreciarse en la parte inferior izquierda de la ventana.

lambda=input('Latitud: ');
lambda=lambda*pi/180;
N=input('Número de día: ');
h=12;

%declinación
x=2*pi*(N-1-(h-12)/24)/365;
delta=0.006918-0.399912*cos(x)+0.070257*sin(x)-0.006758*cos(2*x)

+0.000907*sin(2*x)-0.002697*cos(3*x)+0.001480*sin(3*x);
hr=acos(-tan(lambda)*tan(delta)); %angulo horario del orto u ocaso
alfa_s=@(w) asin(cos(lambda)*cos(w)*cos(delta)+sin(lambda)*sin(delta));
gamma_c=@(w) acos((cos(lambda)*sin(delta)-cos(w)*sin(lambda)*cos(delta))
./cos(alfa_s(w)));
hold on
hMax=floor(hr*12/pi); %hora del orto u ocaso, sin decimales

%desde el orto al mediodía
h=-hMax:0;
w=h*pi/12; %convierte hora en radianes
a_s=alfa_s(w);
g_c=gamma_c(w);
x=cos(a_s).*sin(g_c);
y=cos(a_s).*cos(g_c);
z=sin(a_s);
plot3(x,y,z,'-ro','markersize',6, 'markerfacecolor','y');

%desde el mediodía al ocaso
h=0:hMax;
w=h*pi/12;
a_s=alfa_s(w);
g_c=2*pi-gamma_c(w);
x=cos(a_s).*sin(g_c);
y=cos(a_s).*cos(g_c);
z=sin(a_s);
plot3(x,y,z,'-ro','markersize',6, 'markerfacecolor','y');

plot3([0 0],[-0.4 0.6],[0 0],'k')
xlabel('x')
ylabel('y')
zlabel('z')
title('Posición del Sol')
hold off
view(-126,32)

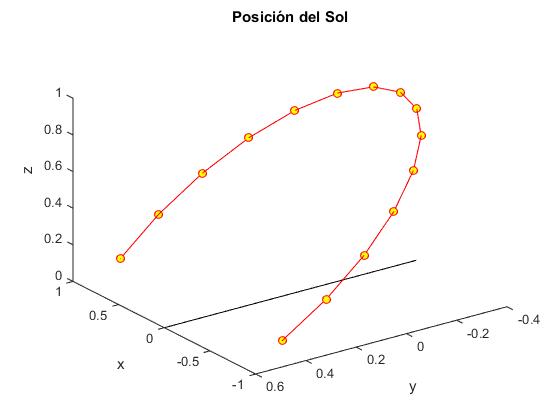
Analema

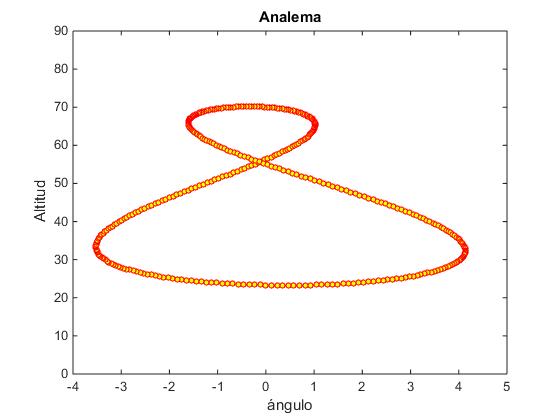
Si dibujamos la altitud del Sol en función del acimut en un determinado momento y en una localidad dada, obtendremos una figura similar a un ocho.

Como hemos visto, la ecuación del tiempo nos da la diferencia entre el movimiento del Sol (medio) y el actual, en el cual se tiene en cuenta que la órbita de la Tierra es elíptica y el eje de la Tierra está inclinado respecto a la perpendicular a la eclíptica.

A las 12 del mediodía el Sol alcanza su altura máxima α_sm=90-λ+δ, cuando su acimut γ_s es 180º. A lo largo de los 365 días del año, la hora local del mediodía no es constante debido a la corrección que introduce la ecuación del tiempo. (No tenemos en cuenta los adelantos horarios para ahorrar energía, que cambian la hora local en una hora durante medio año).

Si situamos nuestra cámara fotográfica en la misma posición y tomamos una fotografía del Sol a la misma hora local, superponemos las fotografías, veremos la figura de un ocho. Convertimos el tiempo Δt en minutos que nos suministra la ecuación del tiempo en desviación angular en grados teniendo en cuenta que 60 minutos, o una hora son 15 grados.

Δt=229.18·(0.00075+0.001868·cos(x)-0.032077·sin(x)-0.014615·cos(2x)-0.040849·sin(2x))

Donde x se define en función del número de día N y la hora h

${\displaystyle x=\frac{2\pi }{365}\left(N-1+\frac{h-12}{24}\right)}$

El script realiza las siguientes tareas:

1. Introduce mediante el comando input la latitud λ del lugar
2. Define una función anónima que calcula el tiempo Δt en minutos, cuando se le pasa el parámetro x relacionado con el número de día N a lo largo del año.
3. Define una función anónima que calcula la declinación δ, cuando se le pasa el parámetro x relacionado con el número de día N a lo largo del año.
4. Determina la desviación angular en grados a los que equivale el tiempo Δt
5. Determima la máxima altitud del Sol al mediodía α_sm=90-λ+δ,
6. Representa mediante el comando plot, la desviación angular en el eje horizontal y la altitud máxima en el vertical

En la figura, se muestra la analema para la latitud λ=43.3° de Bilbao

lambda=input('Latitud: ');
lambda=lambda*pi/180;
h=12;

%ecuación del tiempo en minutos
eq_time=@(x) 229.18*(0.000075+0.001868*cos(x)-0.032077*sin(x)
-0.014615*cos(2*x)-0.040849*sin(2*x));
%declinación
delta=@(x) 0.006918-0.399912*cos(x)+0.070257*sin(x)-0.006758*cos(2*x)
+0.000907*sin(2*x)-0.002697*cos(3*x)+0.001480*sin(3*x);

%convierte minutos a grados
N=1:365;
x=2*pi*(N-1-(h-12)/24)/365;
alfa=90-(lambda-delta(x))*180/pi;
gamma=eq_time(x)*15/60; %60 minutos, 1 hora son 15 grados
plot(gamma,alfa,'-ro','markersize',4, 'markerfacecolor','y');

ylim([0 90])
xlabel('ángulo')
ylabel('Altitud')
title('Analema')

Referencia

Sproul A. B. Derivation of solar geometric relationship using vector analysis. Renewable Energy. 32 (2007) 1187-1205.