La ecuación del tiempo
Inclinación del eje de la Tierra
En la página titulada El giróscopo estudiamos el movimiento de precesión de una peonza
Esta descripción es aproximada, siempre que la velocidad angular ω, sea grande en comparación con la velocidad angular de precesión Ω.
Un análisis más detallado del problema indica que el sólido tiene tres movimientos:
- De rotación alrededor de su eje principal de inercia con velocidad angular ω
- De precesión alrededor del eje vertical Z, con velocidad angular Ω
- De nutación o de oscilación del eje vertical entre dos círculos.
No solamente el movimiento de rotación contribuye al momento angular , como hemos supuesto, sino también y en menor medida, los movimientos de precesión y de nutación, esto es lo que hace difícil el análisis detallado de este sistema mecánico.
Los fenómenos giroscópicos tienen muchas aplicaciones: la tendencia de un giróscopo a mantener el eje de rotación fijo en el espacio en ausencia de momento es utilizado en la estabilización de los barcos y en los pilotos automáticos de los aviones.
Otro ejemplo interesante es la precesión de los equinocios. El plano del ecuador hace un ángulo de 23.45° con el plano de la órbita terrestre o eclíptica. La intersección de los dos planos es la línea de los equinoccios. La Tierra es un giróscopo gigante cuyo eje de rotación precesa alrededor del eje perpendicular al plano de la eclíptica con un periodo de 27 725 años. La precesión de los equinocios se debe al momento de las fuerzas ejercido por el Sol y la Luna sobre la Tierra. El eje de la Tierra experimenta también una nutación con una amplitud de 9.2" y un periodo de oscilación de 19 años.
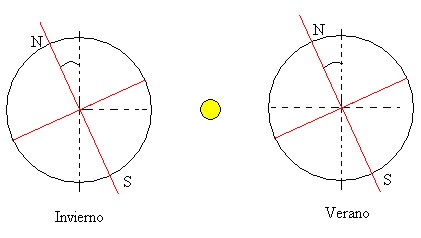
A lo largo de un intervalo de tiempo de varios años (pequeño comparado con el periodo de precesión de 27725 años) podemos considerar que el eje de la Tierra permanece fijo apuntando al mismo lugar en el cielo, la estrella Polar. Pero a medida que la Tierra gira alrededor del Sol siguiendo la órbita elíptica, el ángulo de declinación formando por el plano de la eclíptica y el plano del ecuador va cambiando. En la figura, se representa el mínimo y el máximo que corresponden a las fechas 21 de diciembre y 21 de junio denominadas respectivamente, solsticio de invierno y solsticio de verano en el hemisferio norte. Ambos planos (declinación nula) coinciden en las fechas de 20 de marzo y 22 de septiembre.
El ángulo de declinación es el ángulo formado por los rayos de sol con el plano ecuatorial de la Tierra, es también la latitud a la cual los rayos de sol inciden perpendicularmente a la superficie terrestre a mediodía. El ángulo es positivo cuando el Sol está por encima del ecuador (figura de la derecha) y negativo (figura de la izquerda) cuando el Sol está por debajo del ecuador. En la siguiente dirección se puede encontrar una tabla de ángulos de declinación para cada día de año. Table of the Declination of the Sun.
La declinación solar δ se calcula mediante la siguiente fórmula
δ=0.006918-0.399912·cos(x)+0.070257·sin(x)-0.006758·cos(2x)+0.000907·sin(2x)-0.002697·cos(3x)
+0.001480·sin(3x).
N es el número de día y h la hora. Véase, General Solar Position calculations (NOAA)
La tabla siguiente proporciona la conversión de día del mes d a número de día N en el año
| Mes | Número de día, N |
|---|---|
| Enero | d |
| Febrero | d+31 |
| Marzo | d+59 |
| Abril | d+90 |
| Mayo | d+120 |
| Junio | d+151 |
| Julio | d+181 |
| Agosto | d+212 |
| Septiembre | d+243 |
| Octubre | d+273 |
| Noviembre | d+304 |
| Diciembre | d+334 |
En caso de año bisiesto se añadirá uno más a partir del mes de Marzo. Por ejemplo en la casilla Marzo se pondría d+60, en la casilla Abril d+91, etc.
Mediante el siguiente script representamos la declinacion δ en grados en función de N (1-365) el día del año. Tómese h=12.
h=12;
N=1:365;
x=2*pi*(N-1-(h-12)/24)/365;
delta=(0.006918-0.399912*cos(x)+0.070257*sin(x)-0.006758*cos(2*x)
+0.000907*sin(2*x)-0.002697*cos(3*x)+0.001480*sin(3*x))*180/pi;
plot(N,delta,'r')
line([0 365],[23.45 23.45])
line([0 365],[-23.45 -23.45])
xlim([0 365])
set(gca,'XTick',[15 46 74 105 135 166 196 227 258 288 319 349])
mes = ['Ene';'Feb';'Mar';'Abr';'May';'Jun';'Jul';'Ago';'Sep';'Oct';
'Nov';'Dec'];
set(gca,'XTickLabel',mes)
grid on
ylabel('\delta grados')
title('Declinación a lo largo del año')
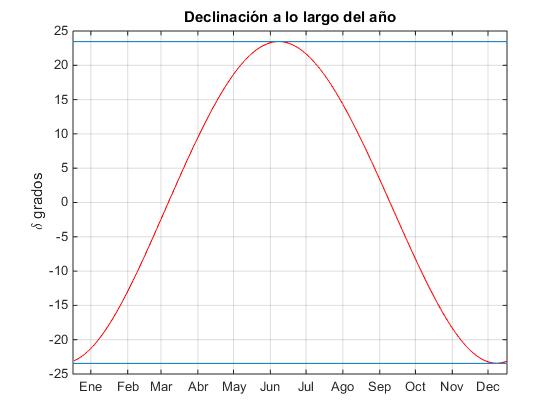
En el script se ha cambiado las divisiones del eje X por defecto, sustituyéndolas por los días 15 de cada mes.
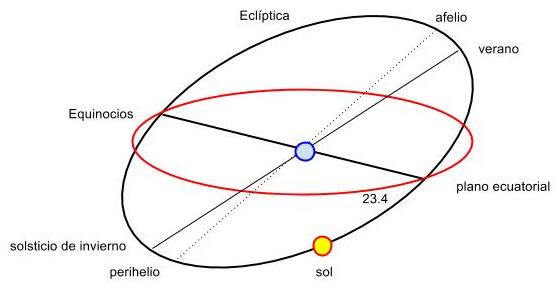
Así pues, la inclinación del eje de la Tierra respecto de la perpendicular al plano de la eclíptica de 23.45° es la responsable de la sucesión de las estaciones. La rotación de la Tierra alrededor de su eje es la responsable de la sucesión de los días y las noches.
La Tierra se mueve alrededor del Sol en una órbita elíptica cuyo periodo es 365.25 días. La distancia media entre el Sol y la Tiera es 1.496·1011 m (una unidad astonómica UA). El plano de la órbita se denomina eclíptica.
- La distancia más alejada del Sol se denomina afelio de 152 097 525 km y ocurre el 5 de julio
- La distancia más cercana al Sol, se denomina perihelio y ocurre alrededor del 2 de enero cuando la Tierra está a una distancia del Sol de 147 097 984 km
- El ángulo de declinación δ=23.45° se denomina solsticio de verano y ocurre el 21 de junio a las 07h 04m (inicio del verano)
- El ángulo de declinación δ=-23.45° se denomina solsticio de invierno y ocurre el 21 de diciembre a las 18h 11m (inicio del invierno)
- El ángulo de declinación δ=0° se denomina equinocios y ocurren el 20 de marzo a las 12h 02m (inicio de la primavera) y 22 de septiembre a las 22h 44m (inicio del otoño)
Véase la web del Ministerio de Fomento: "Efemérides y fenomenos astronómicos relevantes en el año 2013"
Hora local y hora solar
El paso del tiempo se mide a partir de la rotación de la Tierra alrededor de su eje, una vuelta cada día. Todos las localidades que están en un meridiano tienen la misma hora. Se toma como referencia el meridiano que pasa por Greenwich (Inglaterra). El Tiempo Universal está definido dividiendo el día en 24 horas y tomando como hora cero a medianoche.
Latitud y longitud de un lugar
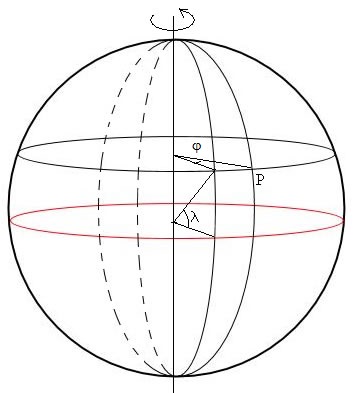
La posición de un punto sobre la superficie de la Tierra se mide mediante una latitud λ y una longitud φ. La latitud va de 0 en el Ecuador a ±90°, hacia el norte las latitudes son positivas y hacia el sur negativas. La longitud de 0 a ±180° se mide tomando como referencia el meridiano que pasa por Greenwich, hacia el Este las longitudes son positivas y hacia el Oeste las longitudes son negativas.
Google Maps proporciona la latitud y longitud de cualquier localidad. Por ejemplo situamos el cursor sobre Eibar (País Vasco) y pulsamos el botón derecho del ratón. En el menú que aparece seleccionamos ¿Qué hay aquí?. En el control de edición situado en la parte superior izquierda aparece la latitud y longitud, tal como apreciamos en la figura.
Dado que Eibar está en el hemisferio norte, la latitud 43.19° es positiva y como está está al Oeste del meridiano 0 o de Greenwich la longitud es -2.49, negativa.
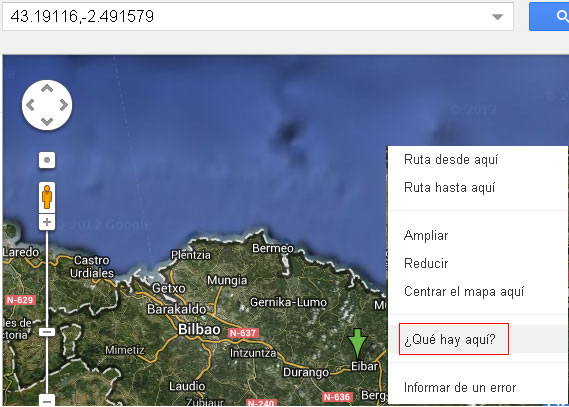
Introducimos las coordenadas (latitud, longitud) del lugar en dicho control de edición y Google maps nos lo muestra. Se suguiere poner Google maps en baja resolución (el cursor de la barra de resolución hacia -).
Hora local
La duración variable del día se debe a las siguientes causas, solamente las dos primeras son importantes:
- La Tierra describe una órbita alrededor del Sol que no es circular, de modo que la Tierra tiene una velocidad mayor cuando está cerca del Sol y una velocidad menor cuando está lejos, de acuerdo con la ley de las áreas de Kepler.
- El eje de la Tierra está inclinado respecto de la perpendicular al plano de la eclíptica 23.45°.
- La velocidad angular de rotación de la Tierra alrededor de su eje va disminuyendo con el tiempo, debido al efecto de las fuerzas de marea ejercidas por la Luna.
- El eje de la Tierra también describe un movimiento de nutación
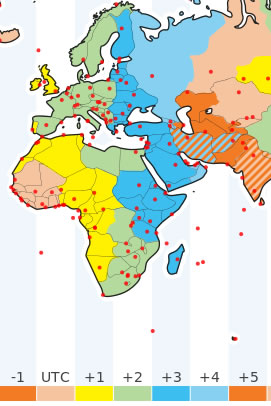
La Tierra se divide en zonas de anchura 15 grados tomadas desde el meridiano cero. Cada zona tiene la misma hora y se diferencia en una hora de la siguiente. Sin embargo, esta no es una regla general y como podemos ver en la figura tomada de la web Time and Date, España peninsular tiene la misma hora que Europa central, a pesar de que el oeste de Galicia está a -9° de longitud y el este de Polonia a 23.5° de longitud por lo que la anchura de esta zona horaria es de 31.5° el doble de una standard. Inglaterra, Portugal y Canarias tienen una hora menos.
Situando el cursor sobre el punto rojo que representa Madrid obtenemos la hora, por ejemplo 23:00:28. Pinchando en el punto obtenemos información suplementaria. Que Madrid está en la zona UTC/GMT+1, además aplica un adelanto horario para ahorrar energía (Daylight saving time) por lo que la hora local de Europa central CEST (Central European Summer Time) es UTC/GMT+2.
El adelanto horario, empieza el último domingo de Marzo y acaba el último domingo de Octubre. Ello viene regulado por la Directiva 2000/84/CE del Consejo de la Comunidad Europea. El horario adelantado para el año 2013 se inicia a las 2h de la madrugada (hora peninsular) del domingo 31 de marzo, momento en que los relojes se adelantarán una hora y durará hasta las 3 h de la madrugada (hora peninsular) del domingo 27 de octubre, momento en que los relojes se retrasarán una hora.
La ecuación del tiempo
En la página titulada El problema de Kepler vimos la dificultad para calcular la posición angular θ de un satélite artificial o de un planeta en el instante t. Véase Equation of Time. Problem in Astronomy. M. Muller.
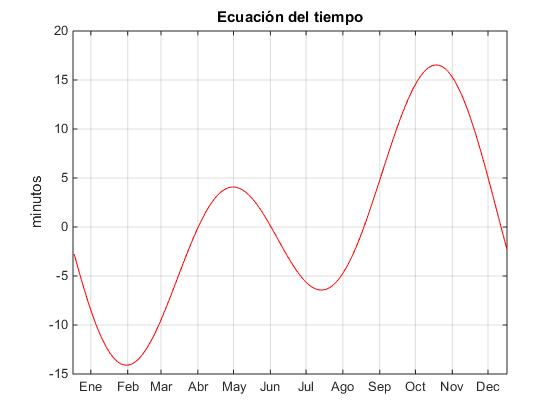
El movimiento aparente del Sol no es uniforme y la duración del día solar no es constante a lo largo del año. La diferencia entre el movimiento aparente del Sol y el movimiento medio se denomina ecuación del tiempo. La expresión tomada de General Solar Position calculations (NOAA) nos da la ecuación del tiempo en minutos
Δt=229.18·(0.000075+0.001868·cos(x)-0.032077·sin(x)-0.014615·cos(2x)-0.040849·sin(2x))
Donde x se define en función del número de día N y la hora h
Mediante el siguiente script representamos la ecuación del tiempo en minutos en función de N (1-365) el día del año. Tómese h=12. Cambiar las divisiones del eje X por defecto, sustituyéndolas por los días 15 de cada mes.
h=12;
N=1:365;
x=2*pi*(N-1-(h-12)/24)/365;
y=229.18*(0.000075+0.001868*cos(x)-0.032077*sin(x)-0.014615*cos(2*x)
-0.040849*sin(2*x));
plot(N,y,'r')
xlim([0 365])
set(gca,'XTick',[15 46 74 105 135 166 196 227 258 288 319 349])
mes = ['Ene';'Feb';'Mar';'Abr';'May';'Jun';'Jul';'Ago';'Sep';'Oct';
'Nov';'Dec'];
set(gca,'XTickLabel',mes)
grid on
ylabel('minutos')
title('Ecuación del tiempo')
Hora local y hora solar
La hora solar se fundamenta en que la Tierra da una vuelta completa en 24 horas y que a las 12:00 h el Sol apunta exactamente hacia el sur. La hora solar verdadera se calcula mediante las dos ecuaciones siguientes:
time_offset=eqTime-4·longitude+60·timezone
- eqTime es Δt, la ecuación del tiempo en minutos
- longitude, es la longitud del lugar en grados (un grado de longitud equivale a 4 minutos, ó 15 grados a una hora),
- timezone es el tiempo en horas desde UTC.
La hora solar verdadera tst, en minutos, se obtiene mediante la siguiente ecuación
tst=hr·60+min+seg/60+time_offset
donde hr es la hora (0-23), min es el minuto (0-60) y seg es el segundo (0-60)
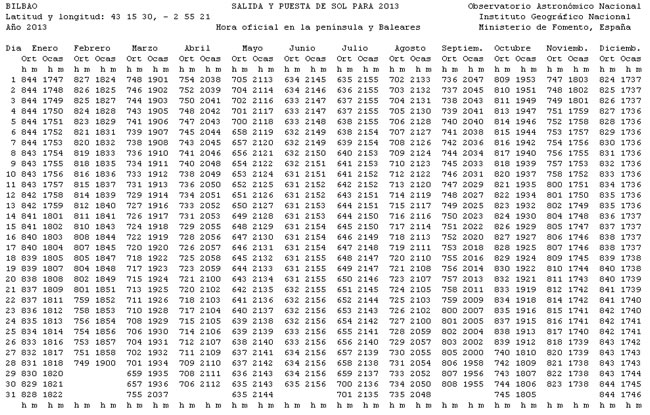
La utilización más importante en las aplicaciones solares es la determinación de la hora local de la salida del Sol, de la puesta del Sol o del mediodía, que por otra parte, disponemos en tablas en la web del Ministerio de Fomento.
Se denomina Orto o salida del Sol al instante que corresponde a la aparición del borde superior del Sol en un horizonte hipotético en que no se considera el relieve del horizonte real, ni obstáculos cercanos (casas, árboles), ni la presencia de nubes o niebla.
El orto real en un lugar dado se puede retrasar en varios minutos si hay elevaciones del terreno en la dirección de salida del Sol, lo cual puede dar lugar a que sobre el terreno se aprecie que el Sol no ha salido pero que ya haya tenido lugar la salida de Sol en el sentido astronómico que generalmente se aplica y que hemos considerado en nuestras tablas.
Del mismo modo, se denomina Ocaso o puesta del Sol al instante que corresponde a la desaparición del borde superior del Sol en un horizonte hipotético en que no se considera el relieve del horizonte real, ni obstáculos cercanos (casas, árboles), ni la presencia de nubes o niebla.
Angulo horario
Para describir la rotación de la Tierra alrededor de su eje se utiliza el concepto de ángulo horario ω.
Como se muestra en la figura, el ángulo horario es la distancia ente el meridiano del observador P y el meridiano cuyo plano contiene al Sol. El ángulo horario es cero al mediodía (cuando el Sol alcanza la máxima altura en el cielo). El Sol apunta hacia el sur pues el plano meridiano del observador contiene al Sol. El ángulo horario se incrementa 15 grados por cada hora.
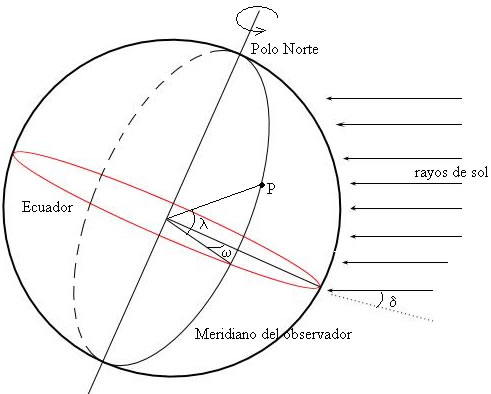
El ángulo horario es -180° a las 0h, 0° a mediodía (12h) y 180° al final del día (24h)
Por ejemplo, tres horas después del mediodía, la hora solar es 15:00 horas y el ángulo horario es de 45°. Dos horas y 20 minutos antes del mediodía el hora solar es 9:40 y ángulo solar es -35°.

