Datos de la Tierra, Júpiter y el Sol

Para resolver este problema se precisan los siguientes datos:

• la constante de la Gravitación Universal, G=6.673·10^-11 N²m²/kg²
• masa del Sol, M_S=1.98·10³⁰ kg,
• la masa de la Tierra, M_T=5.98·10²⁴ kg
• la distancia media entre la Tierra y el Sol, r_T=1.496·10¹¹ m
• el radio de la Tierra, R_T=6.37·10⁶ m
• la masa de la Júpiter, M_J=1.90·10²⁷ kg
• la distancia media entre Júpiter y el Sol, r_J=7.78·10¹¹ m
• el radio de Júpiter, R_J=6.98·10⁷ m
• una Unidad Astronómica, UA=1.496·10¹¹ m

La esfera de influencia de los planetas

Cuando se lanza una sonda espacial desde la Tierra hacia Júpiter, excluyendo la acción de los otros planetas, la sonda pasa por tres etapas distintas:

• La salida bajo la acción de la Tierra y del Sol, siendo predominante la atracción terrestre.
• La fase heliocéntrica, en casi todo el trayecto entre la Tierra y Júpiter
• La llegada a Júpiter, la atracción de Júpiter predomina sobre la atracción del Sol

Siendo d=7.78·10¹¹ m la distancia entre el centro del Sol y el centro de Júpiter.

El radio de la esfera de influencia de un planeta es la distancia al planeta a la que podemos considerar despreciable la atracción del planeta en comparación con la fuerza que ejerce el Sol. Se calcula mediante la fórmula debida a Laplace

${\displaystyle R_e=d{\left(\frac{M}{M_s}\right)}^{2/5}}$

siendo d la distancia entre el Sol y el planeta considerado, M la masa del planeta y M_s la masa del Sol.

Esfera de influencia de la Tierra

Con los datos, Sabiendo que la masa de la Tierra es M=5.98·10²⁴ kg, su radio R_T=6.37·10⁶ m, la distancia entre la Tierra y el Sol es r_T=1.496·10¹¹ m y la masa del Sol M_S=1.98·10³⁰ kg. El radio de influencia de la Tierra es R_e=926.7·10⁶ m o bien 145.5 radios terrestres. El tamaño de las esfera de influencia de la Tierra es muy pequeño comparado con la distancia entre la Tierra y el Sol d=1.49·10¹¹ m=23485 radios terrestres. De modo que, la nave espacial seguirá una trayectoria heliocéntrica determinada casi exclusivamente por las condiciones iniciales en el momento del lanzamiento y la fuerza de atracción del Sol.

En la figura, se representa la fuerza que ejerce el sol F_S y la fuerza que ejerce la Tierra F_T sobre un objeto situado en el interior de la esfera de influencia de la Tierra, en el intervalo -150·R_T a 150·R_T alrededor del centro de la Tierra. La fuerza que ejerce el Sol es prácticamente constante e igual a la que ejerce sobre el centro de la Tierra. La fuerza que ejerce la Tierra es muy pequeña cuando el objeto se encuentra en el borde de la esfera de influencia, en comparación con la que ejerce el Sol, tal como muestran los cálculos más abajo.

RT=6.37e6; %radio de la Tierra
hold on
x=-150:5:-25;
Ft=6.673e-11*5.98e24./(x*RT).^2; %fuerza de atracción de la Tierra
plot(x,Ft, 'b');

x=25:5:150;
Ft=6.673e-11*5.98e24./(x*RT).^2;
plot(x,-Ft, 'b');
x=-150:5:150;
Fs=6.673e-11*1.98e30./(1.496e11+x*RT).^2; %fuerza de atracción del Sol
plot(x,-Fs, 'r');
hold off
grid on
legend('','Tierra','Sol')
xlabel('r/R_T')
ylabel('F_T,F_S')
title('Esfera de influencia de la Tierra')

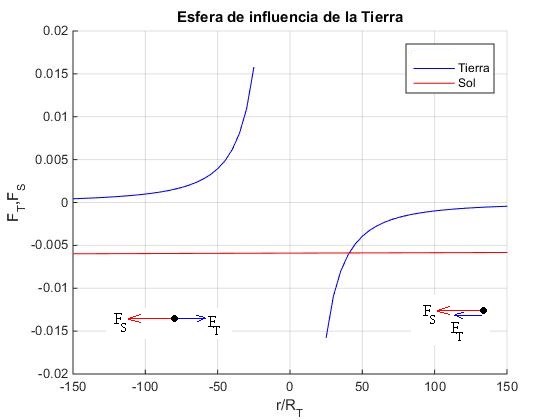
Por ejemplo, si el objeto se encuentra a una distancia para R_e=145.5·R_T =926.7·10⁶ m del centro de la Tierra, a su izquierda o a su derecha. La fuerza que ejerce la Tierra F_T y la que ejerce el Sol F_S es

${\displaystyle \begin{array}{l}{F}_T=6.67·{10}^{-11}\frac{5.98·{10}^{24}·m}{{(926.7·{10}^6)}^2}=4.64·{10}^{-4}m\text{N}\\ F_S=6.67·{10}^{-11}\frac{1.98·{10}^{30}·m}{{(1.496·{10}^{11}-926.7·{10}^6)}^2}=5.97·{10}^{-3}m\text{N}\\ F_S=6.67·{10}^{-11}\frac{1.98·{10}^{30}·m}{{(1.496·{10}^{11}+926.7·{10}^6)}^2}=5.83·{10}^{-3}m\text{N}\end{array}}$

Esfera de influencia de Júpiter

Sabiendo que la masa de Júpiter es M=1.90·10²⁷ kg, su radio R_J=6.98·10⁷ m, la distancia entre Júpiter y el Sol es d=7.78·10¹¹ m y la masa del Sol M_S=1.98·10³⁰ kg. El radio de influencia de Júpiter es R_e=4.83·10¹⁰ m=691.8 radios de Júpiter. El tamaño de las esfera de influencia de la Júpiter es pequeño comparado con la distancia entre la Júpiter y el Sol r_J=7.78·10¹¹ m=11146 radios de Júpiter. De modo que, la nave espacial seguirá una trayectoria heliocéntrica determinada casi exclusivamente por las condiciones iniciales en el momento del lanzamiento y la fuerza de atracción del Sol.

En la figura, se representa la fuerza que ejerce el sol F_S y la fuerza que ejerce Júpiter F_J sobre un objeto situado en el interior de la esfera de influencia de Júpiter, en el intervalo -700R_J a 700·R_J alrededor del centro de Júpiter. La gran extensión de la esfera de influencia de Júpiter y la gran masa de este planeta hacen fuerza que ejerce el Sol no sea constante e igual a la que ejerce sobre el centro de Júpiter, si lo comparamos con el caso de la Tierra. La fuerza que ejerce Júpiter es todavía notable cuando el objeto se encuentra en el borde de la esfera de influencia, en comparación con la que ejerce el Sol, tal como muestran los cálculos más abajo.

RJ=6.98e7; %radio de Júpiter
hold on
x=-600:20:-200;
Fj=6.673e-11*1.90e27./(x*RJ).^2; %fuerza de atracción de Júpiter
plot(x,Fj, 'b');

x=200:20:600;
Fj=6.673e-11*1.90e27./(x*RJ).^2;
plot(x,-Fj, 'b');
x=-600:20:600;
Fs=6.673e-11*1.98e30./(7.78e11+x*RJ).^2; %fuerza de atracción del Sol
plot(x,-Fs, 'r');
hold off
grid on
legend('','Júpiter','Sol')
xlabel('r/R_J')
ylabel('F_J,F_S')
title('Esfera de influencia de Júpiter')

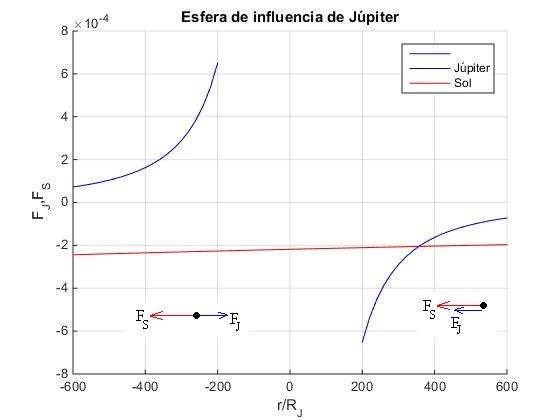
Por ejemplo, si el objeto se encuentra a una distancia para R_e=4.83·10¹⁰ m=691.8·R_J del centro de Júpiter, a su izquierda o a su derecha. La fuerza que ejerce Júpiter F_J y la que ejerce el Sol F_S es

${\displaystyle \begin{array}{l}{F}_J=6.67·{10}^{-11}\frac{1.90·{10}^{27}·m}{{(4.83·{10}^{10})}^2}=5.44·{10}^{-5}m\text{N}\\ F_S=6.67·{10}^{-11}\frac{1.98·{10}^{30}·m}{{(7.78·{10}^{11}-4.83·{10}^{10})}^2}=2.48·{10}^{-4}m\text{N}\\ F_S=6.67·{10}^{-11}\frac{1.98·{10}^{30}·m}{{(7.78·{10}^{11}+4.83·{10}^{10})}^2}=1.93·{10}^{-4}m\text{N}\end{array}}$

Los tamaños de las esferas de influencia son muy pequeños comparados con la distancia entre la Tierra y Júpiter. De modo que la sonda espacial seguirá una trayectoria heliocéntrica determinada casi exclusivamente por las condiciones iniciales en el momento del lanzamiento y la fuerza de atracción del Sol.

Movimiento de la Tierra y de Júpiter alrededor del Sol

Júpiter describe una órbita elíptica cuyo semieje mayor es a=5.203 UA y tiene una excentricidad ε=0.048.

El semieje menor b vale

${\displaystyle b=\sqrt{a^2-c^2}=\sqrt{a^2-a^2{\epsilon }^2}=a\sqrt{1-{\epsilon }^2}=5.197\text{UA}}$

Tomamos como radio medio r de la órbita de Júpiter, la media aritmética R=(a+b)/2=5.20 UA=5.20·1.496·10¹¹ m=7.78·10¹¹ m

Supondremos que Júpiter describe una órbita circular alrededor del Sol cuyo radio r_J

Aplicamos la ecuación de la dinámica del movimiento circular, para calcular la velocidad V_J del planeta alrededor del Sol.

${\displaystyle G\frac{m{M}_S}{r_J^2}=m\frac{V_J^2}{r_J}}$

Despejando la velocidad V_J del planeta

${\displaystyle V_J=\sqrt{\frac{G{M}_S}{r_J}}=\sqrt{\frac{6.67·{10}^{-11}·1.98·{10}^{30}}{7.78·{10}^{11}}}=13028.8\text{m/s}}$

Supondremos igualmente, que la Tierra describe un movimiento circular de radio r_T=1UA=1.496·10¹¹ m. Aplicando la dinámica de movimiento circular uniforme para obtener la velocidad de la Tierra V_T en su movimiento de traslación alrededor del Sol.

${\displaystyle V_T=\sqrt{\frac{G{M}_S}{r_T}}=\sqrt{\frac{6.67·{10}^{-11}·1.98·{10}^{30}}{1.496·{10}^{11}}}=29711.9\text{m/s}}$

Trayectoria de un cuerpo celeste

Cuando una nave espacial se mueve bajo la acción de fuerza de atracción del Sol o de un planeta, describe una trayectoria que es una cónica.

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }\epsilon =\sqrt{1+\frac{2L^{2}E}{G^2{M}^2{m}^3}}d=\frac{L^2}{GM{m}^2}}$

La energía E y momento angular L son constantes por ser la fuerza de atracción central y conservativa

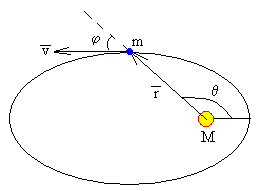
En cualquier punto de la trayectoria, la energía del cuerpo celeste vale

${\displaystyle E=\frac{1}{2}m{v}^2+\left(-G\frac{M_{S}m}{r}\right)}$

y el momento angular

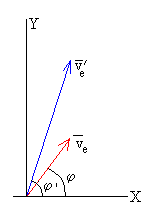
L=m·v·r·sinφ

Siendo φ, el ángulo entre la dirección de la velocidad (tangente a la trayectoria) y la dirección radial, tal como se indica en la figura.

El tipo de trayectoria depende del valor y del signo de la energía total E

• Si E<0 la trayectoria es elíptica
• Si E=0, la trayectoria es parabólica
• Si E>0 la trayectoria es hiperbólica

Movimiento de la sonda espacial desde la Tierra hacia Júpiter

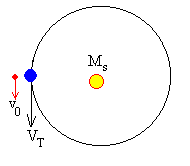
La sonda tiene la velocidad V_T de traslación de la Tierra más una velocidad adicional v₀ en la misma dirección que le proporcionan sus impulsores. La velocidad total de la nave espacial respecto a un Sistema de Referencia ligado al Sol es v_T =V_T+v₀.

Supondremos que esta velocidad adicional se la proporcionamos cuando la sonda está cerca de la Tierra pero fuera de su esfera de influencia.

Conocida la posición y la velocidad de partida, determinaremos la ecuación de la trayectoria heliocéntrica, bajo la única influencia de la fuerza de atracción del Sol. La energía total y el momento angular en el punto de partida valen

${\displaystyle \begin{array}{l}E=\frac{1}{2}m{v}_T^2-G\frac{M_{S}m}{r_T}\\ L=m{r}_T{v}_T\end{array}}$

Si E<0 la sonda espacial describe una trayectoria elíptica, cuyo afelio (máximo alejamiento del Sol) es r_m y cuyo perihelio (máximo acercamiento al Sol) es r_T (el radio de la órbita de la Tierra).

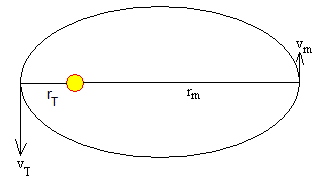
Calculamos la velocidad v_m del satélite en el afelio sabiendo que la energía y del momento angular son constantes en todos los puntos de la trayectoria.

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}_T^2-G\frac{M_{S}m}{r_T}=\frac{1}{2}m{v}_m^2-G\frac{M_{S}m}{r_m}\\ m{r}_T{v}_T=m{r}_m{v}_m\end{array}}$

Si r_m es menor que el radio de la órbita de Júpiter r_J, la nave espacial no alcanza la órbita de Júpiter. Calculamos la velocidad mínima v_T de la nave espacial cuando es lanzada desde la Tierra para que justamente llegue a Júpiter r_m=r_J. Después de hacer algunas operaciones llegamos a la expresión

${\displaystyle v_T=\sqrt{\frac{2G{M}_S{r}_J}{r_T(r_T+r_J)}}}$

Con los datos

• Masa del Sol, M_S=1.98·10³⁰ kg
• Radio de la órbita de Júpiter, r_J=7.78·10¹¹ m
• Radio de la órbita de la Tierra r_T=1.496·10¹¹ m

Se obtiene v_T=38481.7 m/s. Como la velocidad de traslación de la Tierra alrededor del Sol es V_T=29711.9 m/s, la velocidad adicional que deben de proporcionar los impulsores a la nave espacial en el punto de partida tendrá que ser mayor que v₀=v_T-V_T=8769.8 m/s.

Encuentro de la sonda espacial con Júpiter

Calculamos la intersección de la órbita elíptica de la sonda espacial con la órbita circular de Júpiter.

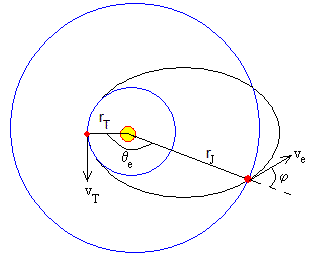
En la ecuación de la trayectoria en coordenadas polares ponemos r=r_J y despejamos el ángulo θ.

${\displaystyle {\theta }_e=\arccos \left(\frac{1}{\epsilon }\left(\frac{d}{r_J}-1\right)\right)}$

Como la energía E es constante en todos los puntos de la trayectoria, obtenemos la velocidad v_e de la sonda espacial en dicha posición de encuentro

${\displaystyle \frac{1}{2}m{v}_T^2-G\frac{M_{S}m}{r_T}=\frac{1}{2}m{v}_e^2-G\frac{M_{S}m}{r_J}}$

De la constancia del momento angular L obtenemos el ángulo φ entre le vector velocidad y la dirección radial (la que une el Sol con el planeta Júpiter)

mr_Tv_T=mv_er_J·sinφ

Tiempo del encuentro

Calculamos el tiempo que tarda la sonda espacial en encontrarse con el planeta Júpiter, empleando la ley de las áreas. El momento angular en coordenadas polares se escribe

${\displaystyle L=m{r}^2\frac{d\theta }{dt}}$

Integrando

${\displaystyle {\displaystyle \underset{0}{\overset{\theta }{\int }}\frac{1}{2}{r}^{2}d\theta }={\displaystyle \underset{0}{\overset{t}{\int }}\frac{L}{2m}dt}}$

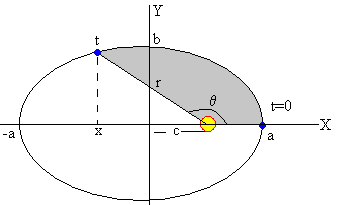
El primer miembro, es el área barrida por el radio vector cuando se mueve desde la posición angular θ=0, a la posición θ, en color gris en la figura. Despejando el tiempo t

${\displaystyle t=\frac{2m·\text{Area}}{L}}$

El área sombreada es el área de la porción de elipse comprendida entre x y a menos el área del triángulo de base r·cos(180-θ) y altura r·sin(180-θ).

Sabiendo que la ecuación de la elipse es

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$

donde a es el semieje mayor de la elipse, b el semieje menor y c la semidistancia focal.

El área de la porción de elipse comprendida entre x y a es

${\displaystyle {\displaystyle \underset{x}{\overset{a}{\int }}b\sqrt{1-\frac{x^2}{a^2}}dx}={\displaystyle \underset{z_1}{\overset{z_2}{\int }}ab{\cos }^{2}z·dz=\frac{ab}{2}{\left[z+\frac{1}{2}\text{sin}2z\right]}_{z_1}^{z_2}}=\frac{ab}{2}\left(\frac{\pi }{2}-z_1-\frac{1}{2}\text{sin}2z_1\right)}$

Para integrar, se ha hecho el cambio de variable x=a·sin z. Los nuevos límites de integración son:

• cuando x=a, z₂=π/2,
• cuando r·cosθ+c=a·sinz₁

El área total es

${\displaystyle \text{Area}=\frac{ab}{2}\left(\frac{\pi }{2}-z_1-\frac{1}{2}\text{sin}2z_1\right)+\frac{r^2\text{sin}2\theta }{4}}$

El instante t_e de encuentro es proporcional al área barrida por el radio vector.

Conocido r y θ,  se calcula el semieje mayor a, que es la media aritmética de los radios mínimo y máximo de la elipse.

${\displaystyle 2a=\frac{d}{1+\epsilon }+\frac{d}{1-\epsilon }}$

La semidistancia focal c=ε·a

El semieje menor b de la elipse $b=\sqrt{a^2-c^2}$

Supongamos que los impulsores proporcionan a la sonda espacial una velocidad adicional de 9200 m/s en el momento de su partida en las proximidades de la Tierra. La velocidad de la sonda medida desde el Sistema de Referencia ligado al Sol es v_T=9200+V_T=38911.9 m/s

Calculamos la energía y el momento angular en el punto de partida

E=-125.73·10⁶·m J, L=5.82·10¹⁵·m kgm²/s

A partir de estos datos, obtenemos el valor del parámetro d y la excentricidad ε de la elipse.

ε=0.715, d=2.57·10¹¹ m

Calculamos la posición del punto de intersección de la trayectoria elíptica de la sonda espacial con la órbita circular de Júpiter, θ_e=159.6º

La constancia de la energía E nos permite calcular la velocidad de la sonda en dicho punto de encuentro, v_e=9383.2 m/s

La constancia del momento angular L nos permite calcular el ángulo que forma dicha velocidad con la dirección Sol-Júpiter, φ=52.9º

El instante en el que se encuentra la sonda y Júpiter es aquél en el que r=r_J=7.78·10¹¹ m y θ=θ_e=159.6º.

Conocida la ecuación de la elipse en coordenadas polares, calculamos a, b, c y z₁ y la introducimos en la expresión del tiempo, resultando t_e=682.4 días

G=6.67e-11; %constante G
MS=1.98e30; %masa del Sol
rJ=7.78e11; %radio de la órbita de Júpiter
rT=1.496e11; %radio de la órbita de la Tierra
vT=sqrt(G*MS/rT);  %velocidad orbital de la Tierra
vJ=sqrt(G*MS/rJ);  %velocidad orbital de Júpiter

v1=9200+vT; % velocidad de la sonda cuando sale de la Tierra 

L=v1*rT; %momento angular
E=v1^2/2-G*MS/rT; %energía
ex=sqrt(1+2*L^2*E/(G*MS)^2) %excentricidad
d=L^2/(G*MS);
a=d/(1-ex^2);  %semieje mayor de la elipse
b=a*sqrt(1-ex^2); %semieje menor
angulo=acos((d-rJ)/(rJ*ex));
ve=sqrt(2*(v1^2/2-G*MS/rT+G*MS/rJ));
phi=asin(rT*v1/(ve*rJ));
z1=asin(rJ*cos(angulo)/a+ex);
area=a*b*(pi/2-z1-sin(2*z1)/2)/2+rJ^2*sin(2*angulo)/4;
t=2*area/L; %tiempo
fprintf('Encuentro con Júpiter: velocidad %4.1f,
 ángulo %2.1f\n', ve,phi*180/pi)
fprintf('Tiempo de viaje (días) %3.1f\n', t/(24*3600))

Encuentro con Júpiter: velocidad 9383.2, ángulo 52.9
Tiempo de viaje  (días) 682.4

Movimiento de la sonda espacial en la esfera de influencia del planeta Júpiter

La sonda espacial entra en la esfera de influencia del planeta Júpiter. Supondremos que la energía potencial debida a la fuerza de atracción del Sol es prácticamente constante en todos los puntos de dicha esfera, por lo que la trayectoria ulterior de la sonda viene determinada exclusivamente por la fuerza de atracción del planeta Júpiter, la velocidad inicial y su dirección en el momento en el que entra en dicha esfera de influencia.

Nos situaremos por tanto, en un Sistema de Referencia ligado al planeta Júpiter, calculamos la velocidad inicial y su dirección en este Sistema de Referencia.

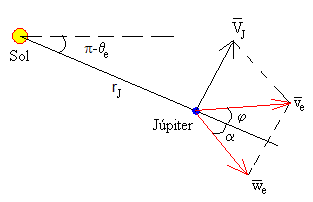
Sea $\overrightarrow{v_e}$ es la velocidad de la sonda espacial medida en el S.R. ligado al Sol, $\overrightarrow{V_J}$ es la velocidad del planeta Júpiter alrededor del Sol. La velocidad $\overrightarrow{w_e}$ de la sonda espacial respecto de un S.R. ligado a Júpiter es.

${\displaystyle \overrightarrow{w_e}=\overrightarrow{v_e}-\overrightarrow{V_J}}$

Descomponemos las velocidades, en la dirección radial (Sol-Júpiter) y en la dirección perpendicular a la radial.

w_e·sinα=v_e·sinφ-V_J
w_e·cosα=v_e·cosφ

Continuando con los datos del apartado anterior, calculamos la velocidad de la nave espacial w_e=7926.2 m/s  y su dirección α=-44.4º  respecto de la recta que une el Sol con Júpiter, medidos en el S.R. ligado a este planeta.

Para determinar la ecuación de la trayectoria calculamos la energía Σ y el momento angular Γ de la sonda espacial en este nuevo S.R.

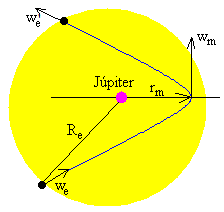
A una distancia de Júpiter igual a su radio de influencia R_e=4.83·10¹⁰ m la velocidad de la sonda espacial es w_e.

${\displaystyle E=\frac{1}{2}m{w}_e^2-G\frac{M_{J}m}{R_e}}$

Para calcular el momento angular, necesitamos un dato más, el parámetro de impacto o la distancia mínima de aproximación r_m de la sonda espacial al centro de Júpiter. Elegimos este segundo parámetro por ser más significativo que el primero.

L=mr_m·w_m·sin90º= mw_m·r_m

Como la energía total Σ es constante en todos los puntos de la trayectoria, la velocidad máxima de la nave espacial en el punto más cercano al planeta es

${\displaystyle E=\frac{1}{2}m{w}_m^2-G\frac{M_{J}m}{r_m}}$

La energía Σ y el momento angular Γ determinan la ecuación de la trayectoria.  La nave espacial describe una trayectoria hiperbólica acercándose al planeta a una distancia r_m, donde alcanza la máxima velocidad y luego, sale de la región de influencia del Júpiter con la misma velocidad inicial w_e pero girada cierto ángulo como veremos a continuación.

Con el dato de la masa de Júpiter M_J=1.90·10²⁷ kg, calculamos la energía total Σ =28.79·10⁶·m J.

Con el dato de la mínima distancia de acercamiento r_m=2.84·R_J radios planetarios o bien r_m=198.2·10⁶ m. calculamos la velocidad de la sonda en dicha posición w_m=36553.8 m/s, y el momento angular Γ= 7.25·10¹²·m kg·m²/s.

Conocida la energía E y el momento angular L la ecuación de la trayectoria es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }\epsilon =\sqrt{1+\frac{2E{L}^2}{G^2{M}_J^2{m}^3}}d=\frac{L^2}{G{M}_J{m}^2}}$

El ángulo que forma la dirección final de la velocidad se calcula poniendo r→∞, con lo que

${\displaystyle {\theta }_L=\arccos \frac{-1}{\epsilon }}$

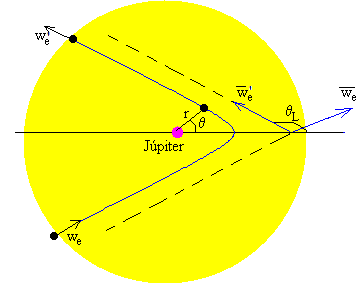
El ángulo que forma la dirección inicial y la dirección final de la velocidad es 2θ_L-π tal como se aprecia en la figura.

Con los datos anteriores de la energía E y del momento angular L tenemos que

ε=1.09, y θ_L=156.5º.

Trayectoria final de la sonda espacial

Una vez que la sonda espacial ha salido de la esfera de influencia del planeta Júpiter, nos situamos en el Sistema de Referencia ligado al Sol.

El eje de la hipérbola hay que girarlo un cierto ángulo para que la velocidad inicial $\overrightarrow{w_e}$ forme un ángulo α con la recta que une el Sol con el planeta Júpiter, tal como se muestra en la figura. La velocidad final $\overrightarrow{w_e^{\text{'}}}$ formará un ángulo α'=2θ_L-π+α con dicha dirección.

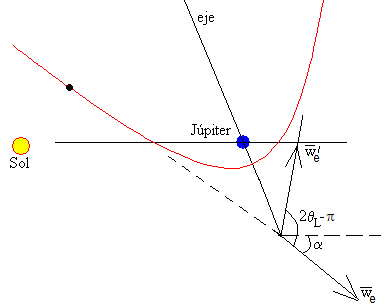
La velocidad final $\overrightarrow{v_e^{\text{'}}}$ de la sonda será la suma vectorial

${\displaystyle \overrightarrow{v_e^{\text{'}}}=\overrightarrow{w_e^{\text{'}}}+\overrightarrow{V_J}}$

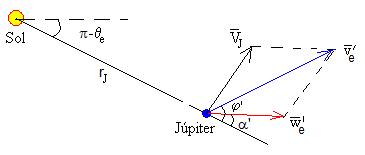
Descomponemos las velocidades, en la dirección radial (Sol-Júpiter) y en la dirección perpendicular a la radial.

${\displaystyle \{\begin{array}{l}{v}_e^{\text{'}}\sin \phi \text{'}=w_e^{\text{'}}\sin \alpha \text{'}+V_J\\ v_e^{\text{'}}\cos \phi \text{'}=w_e^{\text{'}}\cos \alpha \text{'}\end{array}}$

Con los datos α'=2·156.5-180-44.4=88.7º, w'_e=w_e=7926.2 m/s, y V_J=13028.8 m/s, obtenemos

v’_e=20953.8 m/s
φ’=89.5º

La sonda sale de la esfera de influencia de Júpiter con velocidad v’_e, su distancia al Sol es aproximadamente igual a r_J=7.78·10¹¹ m, radio de la órbita de Júpiter. La sonda espacial se mueve bajo acción de fuerza de atracción solar. La energía y el momento angular son

${\displaystyle E\text{'}=\frac{1}{2}mv{\text{'}}^2-G\frac{M_{S}m}{r_J}}$

L’=mv’_er_J·sinφ’

Con los datos anteriores, E’=49.8·10⁶·m J y L’=1.63·10¹⁶·m kgm²/s

La trayectoria es una hipérbola, por que la energía es positiva. La sonda espacial se aleja del Sol para no regresar nunca más.

Estudio energético

En la parte derecha del programa interactivo (más abajo), se ha situado una barra, que muestra los cambios energéticos que experimenta la sonda espacial a lo largo de su trayectoria.

Un cuerpo situado a una UA del centro del Sol tiene una energía potencial negativa igual a

${\displaystyle E_p=-G\frac{M_{S}m}{r_T}=-6.67·{10}^{-11}\frac{1.98·{10}^{30}m}{1.496·{10}^{11}}=-882.8·{10}^6·m\text{J}}$

Para que el cuerpo salga del Sistema Solar hemos de proporcionarle una energía cinética suficiente para que la energía total sea mayor o igual a cero. La velocidad de escape v_e es la velocidad que hay que proporcionar a un cuerpo para que llegue al infinito con velocidad nula.

${\displaystyle E=\frac{1}{2}m{v}_e^2-G\frac{M_{S}m}{r_T}=0v_e=42018.9\text{m/s}}$

No es necesario aportar esta enorme cantidad de energía a la sonda espacial para que visite los planetas exteriores y se aleje del Sistema Solar.

Como la sonda espacial se mueve con la Tierra, si lanzamos la sonda en la dirección tangente a la órbita circular y en el sentido del movimiento de la Tierra, V_T=29711.9 m/s. La velocidad de escape se reduce

${\displaystyle E=\frac{1}{2}m{(v_e+V_T)}^2-G\frac{M_{S}m}{r_T}=0v_e=12307.5\text{m/s}}$

Podemos reducir aún más la velocidad de lanzamiento y por tanto, la energía que aportan los impulsores de la sonda, si aprovechamos el encuentro favorable con un planeta masivo como Júpiter tal como hemos estudiado en esta página.

Ahora bien, como hemos calculado al principio de esta página, para que la sonda espacial llegue desde la Tierra a la órbita de Júpiter es necesario proporcionarle una velocidad superior a 8769.8 m/s

Entre el punto de partida de la sonda espacial, en las cercanías de la Tierra, y en el punto de llegada a las proximidades de Júpiter, la energía total se mantiene constante y su valor, con los datos, que hemos manejado, es

E=-125.73·10⁶·m J

Al salir de la esfera de influencia de Júpiter, la energía final es

E’=49.8·10⁶·m J≥0

que es más que suficiente para que la sonda abandone el Sistema Solar.

• Variación de energía

La diferencia de energía provendrá del planeta en movimiento, cuya velocidad disminuirá de forma inapreciable ya que su masa es muy grande comparada con la masa de la sonda espacial.

${\displaystyle E\text{'}-E=\frac{1}{2}{M}_J{V}_f^2-\frac{1}{2}{M}_J{V}_i^2\approx M_J{V}_J\Delta V_J}$

Si la velocidad orbital de Júpiter es 13028.8 m/s, su masa M_J=1.9·10²⁷ kg y la masa de la sonda espacial es m=260 kg, el cambio de velocidad que experimenta el planeta como consecuencia de su encuentro con la sonda espacial es ΔV_J≈1.84·10^-21 m/s.

• Variación de momento lineal

Considerando el sistema formado por Júpiter y la sonda espacial como aislado en el momento del encuentro, aplicando el principio de conservación del momento lineal, calculamos la variación de velocidad.

${\displaystyle m\overrightarrow{v}\text{'}=m\overrightarrow{v_e}+M_J{\overrightarrow{\Delta V}}_J}$



La velocidad inicial $\overrightarrow{v_e}$ de la sonda espacial al entrar en la esfera de influencia de Júpiter es de 9383.2 m/s y el ángulo que forma con la dirección Sol-Júpiter es φ=52.9º

La velocidad final $\overrightarrow{v_e^{\text{'}}}$ de la sonda al salir de dicha esfera es 20953.8 m/s y el ángulo que forma con la dirección Sol-Júpiter es de φ’=89.5º

Hallamos las componentes de la velocidad en la dirección radial (Sol-Júpiter) y en la dirección perpendicular a la radial.

m·(v’_e·cosφ’-v_e·cosφ)=M_J ·Δv_x
m·(v’_e·sinφ’-v_e·sinφ)=M_J ·Δv_y

${\displaystyle \Delta V_J=\sqrt{\Delta v_x^2+\Delta v_y^2}=2.0·{10}^{-21}\text{m/s}}$

Se obtiene aproximadamente el mismo valor

Actividades

Se introduce

• La velocidad km/s que proporcionan los impulsores a la sonda en el punto de partida situado cerca de la Tierra, en el control titulado Velocidad
• La distancia mínima de aproximación a Júpiter, medida en radios de Júpiter (69.8·10⁶ m), en el control titulado Mínima distancia a Júpiter.

Se pulsa el botón titulado Nuevo.

La velocidad que se introduce ha de ser menor que 12.0 km/s, para que la sonda siga una trayectoria elíptica.

Se observa la trayectoria seguida por la nave espacial en su camino hacia Júpiter desde su lanzamiento en las proximidades de la Tierra.  El planeta Júpiter aparece rodeado de un círculo de color amarillo que nos indica el tamaño relativo de su esfera de influencia.

Si la sonda llega a Júpiter, se cambia al Sistema de Referencia ligado a dicho planeta y se observa la trayectoria hiperbólica de la nave espacial en el interior de su esfera de influencia. No se observa toda la trayectoria, solamente la contenida en la esfera de radio 60 veces el radio de Júpiter. Observamos como el vector velocidad $\overrightarrow{w_e}$ cambia de dirección sin cambiar de módulo

Cuando la sonda espacial sale de la esfera de influencia de Júpiter, se cambia al Sistema de Referencia ligado al Sol y se observa la trayectoria heliocéntrica completa, la inicial desde la Tierra hacia Júpiter y la final desde Júpiter en adelante.

En la parte derecha, observamos los datos de la velocidad de la sonda y del ángulo que forma la velocidad con la dirección Sol-Júpiter. Se indica también los tiempos parciales en cada una de las etapas del movimiento.

La barra coloreada de la derecha, nos muestra los cambios energéticos. La energía potencial es negativa y la energía cinética es positiva. La energía total (la suma de ambas contribuciones) está señalada por un segmento de color claro y su valor viene indicado en millones de julios, ·10⁶·m J. Siendo m la masa de la sonda.

• Velocidad 8.8 km/s
• Mínima distancia de acercamiento a Júpiter 3.84 radios del planeta.

Referencias

Van Allen J. Gravitational assist in celestial mechanics- a tutorial. Am. J. Phys. 71 (5) May 2003, pp. 448-451.