Fuerza de atracción entre los cuerpos

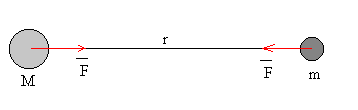
La interacción entre dos cuerpos de masa M y m se describe en término de una fuerza atractiva, cuya dirección es la recta que pasa por el centro de los dos cuerpos y cuyo módulo viene dado por la expresión

$F = G \frac{M m}{r^{2}}$

G es la constante de la gravitación universal G=6.67·10^-11 Nm²/kg² y r es la distancia entre los centros de los cuerpos

Fuerza conservativa

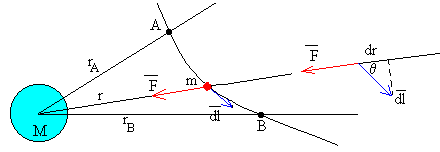
Supongamos que una partícula de masa m se mueve desde la posición A hasta la posición B en las proximidades de un cuerpo fijo de masa M. Vamos a calcular el trabajo realizado por la fuerza de atracción

$\vec{F} = - \frac{G M m}{r^{2}} \hat{r}$

El trabajo infinitesimal dW es el producto escalar del vector fuerza $\vec{F}$ por el vector desplazamiento $\vec{dl}$ , tangente a la trayectoria.

dW=F·dl·cos(180-θ)=-F·dl·cosθ=-F·dr.

donde dr es el desplazamiento infinitesimal de la partícula en la dirección radial.Para calcular el trabajo total, integramos entre la posición inicial A, distante r_A del centro de fuerzas y la posición final B, distante r_B del centro fijo de fuerzas.

$W = \int_{A}^{B} - G \frac{M m}{r^{2}} d r = G \frac{M m}{r_{B}} - G \frac{M m}{r_{A}} = (- G \frac{M m}{r_{A}}) - (- G \frac{M m}{r_{A}})$

El trabajo W no depende del camino seguido por la partícula para ir desde la posición A a la posición B.

La fuerza de atracción $\vec{F}$ , que ejerce el cuerpo fijo de masa M sobre la partícula de masa m es conservativa. La fórmula de la energía potencial es

$E_{p} = \frac{- G M m}{r}$

El nivel cero de energía potencial se ha establecido en el infinito, para r=∞, E_p=0

El hecho de que la fuerza de atracción sea conservativa, implica que la energía total (cinética más potencial) de la partícula es constante, en cualquier punto de la trayectoria.

$E = \frac{1}{2} m v^{2} + E_{p} = cte$

Ejemplo

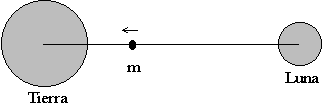
Un satélite artificial cae hacia la Tierra desde una altura de 150 000 km. Calcular:

la fuerza sobre el satélite de 100 kg.
la velocidad de impacto sobre la superficie de la Tierra,

Se supone que el satélite parte del reposo.

Datos: La distancia entre los centros de la Tierra y de la Luna es d=384 000 km. Radio de la Tierra R_T=6370 km. Masa de la Tierra M_T=5.98 10²⁴ kg. Masa de la Luna M_L=7.34 10²² kg. Constante G=6.67 10^-11 Nm²/kg².

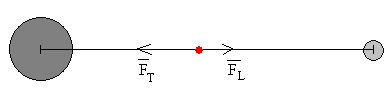
Todas las distancias han de estar referidas al centro de la Tierra y al centro de la Luna

$\begin{array}{l} F_{T} = 6.67 \cdot 10^{- 11} \frac{5.98 \cdot 10^{24} \cdot 100}{{(1.5 \cdot 10^{8} + 6.37 \cdot 10^{6})}^{2}} \\ F_{L} = 6.67 \cdot 10^{- 11} \frac{7.34 \cdot 10^{22} \cdot 100}{{(3.84 \cdot 10^{8} - 1.5 \cdot 10^{8} - 6.37 \cdot 10^{6})}^{2}} \\ F_{T} - F_{L} = 1.62 N \end{array}$

La fuerza resultante está dirigida hacia el centro de la Tierra

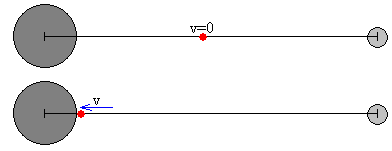
Para calcular la velocidad de impacto aplicamos el principio de conservación de la energía

$\begin{array}{l} (- 6.67 \cdot 10^{- 11} \frac{5.98 \cdot 10^{24} \cdot 100}{1.5 \cdot 10^{8} + 6.37 \cdot 10^{6}}) + (- 6.67 \cdot 10^{- 11} \frac{7.34 \cdot 10^{22} \cdot 100}{3.84 \cdot 10^{8} - 1.5 \cdot 10^{8} - 6.37 \cdot 10^{6}}) = \\ \frac{1}{2} 100 v^{2} + (- 6.67 \cdot 10^{- 11} \frac{5.98 \cdot 10^{24} \cdot 100}{6.37 \cdot 10^{6}}) + (- 6.67 \cdot 10^{- 11} \frac{7.34 \cdot 10^{22} \cdot 100}{3.84 \cdot 10^{8} - 6.37 \cdot 10^{6}}) \end{array}$

v=10959.65 m/s

Fuerza central

La fuerza de atracción entre un planeta y el Sol es central y conservativa.

Una fuerza es central, cuando el vector posición $\vec{r}$ es paralelo al vector fuerza $\vec{F}$ . El momento de la fuerza $\vec{M} = \vec{r} \times \vec{F} = 0$ . De la relación entre le momento de las fuerzas que actúa sobre la partícula y el momento angular, (Teorema del momento angular) se concluye que

$\vec{M} = \frac{d \vec{L}}{d t} \vec{M} = 0 \vec{L} = c t e$

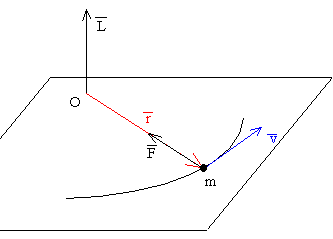
El momento angular permanece constante en módulo, dirección y sentido. El momento angular de una partícula es el vector resultado del producto vectorial $\vec{L} = \vec{r} \times m \vec{v}$ , cuya dirección es perpendicular al plano determinado por el vector posición $\vec{r}$ y el vector velocidad $\vec{v}$ . Como el vector $\vec{L}$ permanece constante en dirección, $\vec{r}$ y $\vec{v}$ estarán en un plano perpendicular a la dirección fija de $\vec{L}$ .

De aquí, se concluye que la trayectoria del móvil estará contenida en un plano perpendicular al vector momento angular $\vec{L}$ .

Cuando los vectores $\vec{r}$ y $\vec{v}$ son paralelos, es decir, la dirección del movimiento pasa por el origen, el momento angular $\vec{L} = 0$ . La partícula describe un movimiento rectilíneo, cuya aceleración no es constante.

Fuerza central y conservativa

En esta sección continuamos con la aplicación de las características de la fuerza de atracción: central y conservativa

Apogeo y perigeo

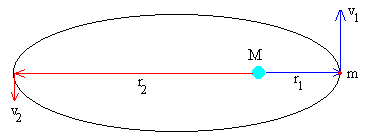
En la figura, se muestra un cuerpo que describe una trayectoria elíptica alrededor del centro de fuerzas situado en uno de sus focos. La distancia de máximo acercamiento es r₁ y la de máximo alejamiento r₂. Las velocidades que lleva el cuerpo en estas dos posiciones extremas son v₁ y v₂ respectivamente. La constancia del momento angular y de la energía nos permite relacionar estas cuatro magnitudes.

$\begin{array}{l} m r_{1} v_{1} = m r_{2} v_{2} \\ \frac{1}{2} m v_{1}^{2} - \frac{G m M}{r_{1}} = \frac{1}{2} m v_{2}^{2} - \frac{G m M}{r_{2}} \end{array}$

Se pueden plantear dos problemas :

Conocido r₁ y r₂ calcular v₁ y v₂.

Se despeja v₁ en la primera ecuación y se sustituye en la segunda. Obtenemos

$v_{2} = \sqrt{\frac{2 G M r_{1}}{r_{2} (r_{1} + r_{2})}} v_{1} = \sqrt{\frac{2 G M r_{2}}{r_{1} (r_{1} + r_{2})}}$

Conocido r₁ y v₁ calcular r₂ y v₂.

Conocida la posición r₁ y la velocidad v₁ en el momento del lanzamiento, aplicando la constancia de la energía y del momento angular, calculamos la velocidad v₂ y distancia r₂ al centro de fuerzas. Después de algunas operaciones, obtenemos la velocidad v₂ en función de r₁ y v₁

$v_{2} = \frac{2 G M}{r_{1} v_{1}} - v_{1}$

Ejemplo

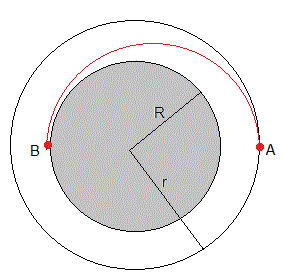
Una nave espacial de masa m=12000 kg, describe una órbita circular alrededor de la Luna a h=100 km de altura sobre su superficie. Para aterrizar en el punto B de la superficie de la Luna, activa su motor de frenado en A durante un intervalo pequeño de tiempo disminuyendo su velocidad. La nave espacial describe una órbita elíptica, cuyo foco se encuentra en el centro de la Luna, que conecta los puntos A y B. Calcular

La velocidad de la nave espacial en su órbita circular
La velocidad de la nave espacial en la posición A (después de activar el motor de frenado) y B de trayectoria elíptica

Datos: constante G=6.67·10^-11 Nm²/kg², masa de la Luna M=7.34·10²² kg, radio de la Luna R_L=1.74·10⁶ m, velocidad de los gases expulsados del cohete, respecto de la nave espacial, u=10000 m/s

Problema de la XI Olimpiada Internacional de Física. Moscú, 1979

La nave espacial describe un movimiento circular de radio r, bajo la acción de la fuerza de atracción de la Luna. Aplicamos la ecuación de la dinámica del movimiento circular uniforme.

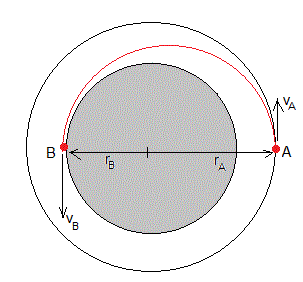
$G \frac{M m}{r^{2}} = m \frac{v_{0}^{2}}{r} v_{0} = \sqrt{G \frac{M}{R_{L} + h}}$

La fuerza de atracción de la Luna es central y conservativa. El momento angular es constante y la energía es constante

$\begin{array}{l} m v_{A} r_{A} = m v_{B} r_{B} \\ \frac{1}{2} m v_{A}^{2} + (- G \frac{M m}{r_{A}}) = \frac{1}{2} m v_{B}^{2} + (- G \frac{M m}{r_{B}}) \end{array}$

Con r_A=R_L+h y r_B=R_L, despejamos v_A y v_B del sistema de dos ecuaciones con dos incógnitas

$\begin{array}{l} v_{A} = \sqrt{2 G \frac{M r_{B}}{r_{A} (r_{A} + r_{B})}} = v_{0} \sqrt{\frac{2 r_{B}}{(r_{A} + r_{B})}} \\ v_{B} = \frac{r_{A} v_{A}}{r_{B}} = \sqrt{2 G \frac{M r_{A}}{r_{B} (r_{A} + r_{B})}} \end{array}$

Con los datos del problema, v₀=1631.2 m/s, v_A=1608.2 m/s, v_B=1700.7 m/s

Velocidad de escape

Se denomina velocidad de escape v_e de una partícula que está a una distancia r₁ del centro de fuerzas, a la velocidad que hemos de proporcionarle para que llegue al infinito con velocidad nula

$\frac{1}{2} m v_{e}^{2} - \frac{G m M}{r_{1}} = 0 v_{e}^{2} = \frac{2 G M}{r_{1}}$

Por ejemplo, la velocidad de escape de la superficie de la Tierra es r₁=6.37·10⁶ m, M=5.98·10²⁴ kg es v_e=11190.7 m/s

Expresamos la velocidad v₂ en términos de la velocidad de escape v_e

$v_{2} = \frac{v_{e}^{2}}{v_{1}} - v_{1}$

Obtenemos la distancia r₂ al centro de fuerzas a partir de la constancia del momento angular

$r_{2} = \frac{r_{1} v_{1}}{v_{2}} = r_{1} \frac{v_{1}^{2}}{v_{e}^{2} - v_{1}^{2}}$

Movimiento circular

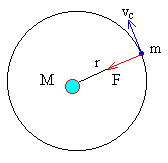
Si el satélite es lanzado con una velocidad v_c tal que

$m \frac{v_{c}^{2}}{r} = \frac{G M m}{r^{2}}, v_{c} = \sqrt{\frac{G M}{r}}$

describirá una órbita circular de radio r.

Se denomina satélite geoestacionario, a aquél cuyo periodo es el mismo que el de rotación de la Tierra. Inmóvil sobre el observador terreste

$P = \frac{2 π r}{v_{c}} r^{3} = \frac{G M P^{2}}{4 π^{2}}$

Sea P=24 h, r=4.225·10⁷ m, la altura del satélite h=r-6.37·10⁶=35880 km

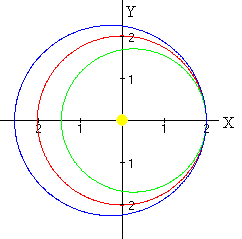
En el caso de los satélites artificiales que circundan la Tierra

Si la velocidad de lanzamiento v₁ es inferior a v_c el punto de lanzamiento es el apogeo.
Si la velocidad de lanzamiento v₁ es mayor que v_c el punto de lanzamiento es el perigeo.

En la figura, la trayectoria de color rojo es circular.