Órbita de transferencia de Hohmann

Transferencia mediante una órbita elíptica

Supongamos que queremos enviar una nave espacial desde la órbita de un planeta a la de otro o bien, elevar un satélite de comunicaciones desde una órbita circular ecuatorial de baja altura a otra órbita coplanar y circular de mayor altura.

Para economizar el combustible, es necesario que la nave espacial siga una trayectoria semielíptica denominada órbita de transferencia de Hohmann para lo que es necesario proporcionarle dos impulsos:

En el punto A cuando la nave espacial pasa de la órbita circular interior a la órbita de transferencia.
En la posición B, cuando la nave espacial pasa de la órbita de transferencia a la órbita circular exterior.

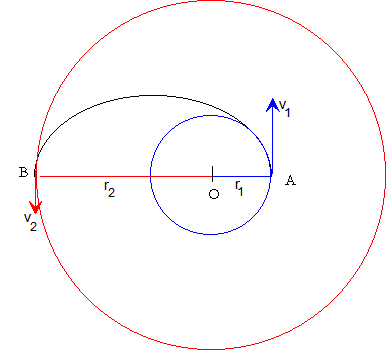
Para resolver el problema propuesto, solamente es necesario hacer uso de las propiedades central y conservativa de la fuerza de atracción que hemos estudiado en páginas anteriores y de la dinámica del movimiento circular uniforme.

Órbita circular interior

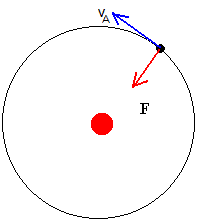
Cuando la nave espacial describe una órbita circular de radio r₁, el módulo de la velocidad v_A se puede calcular aplicando la dinámica del movimiento circular uniforme

$\frac{G M m}{r_{1}^{2}} = m \frac{v_{A}^{2}}{r_{1}} v_{A}^{2} = \frac{G M}{r_{1}}$

Donde M es la masa de la Tierra, G es la constante de la gravitación universal y m es la masa de la nave que se simplifica en las ecuaciones del movimiento.

La energía E₁ de la nave espacial en la órbita circular inicial es

$E_{1} = \frac{1}{2} m v_{A}^{2} - \frac{G M m}{r_{1}} = - \frac{G M m}{2 r_{1}}$

la mitad de la energía potencial

Órbita semielíptica de transferencia

Para calcular la velocidad que debe llevar la nave espacial en el punto A para que alcance la órbita exterior en B, basta aplicar las propiedades central y conservativa de la fuerza de atracción.

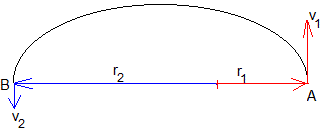
Por la propiedad de la fuerza central, el momento angular es constante y por tanto, tiene el mismo valor en A que en B

$m r_{1} v_{1} = m r_{2} v_{2}$

Por la propiedad de fuerza conservativa, la energía es constante en todos los puntos de la trayectoria y en particular, es la misma en A que en B.

$\frac{1}{2} m v_{1}^{2} - \frac{G M m}{r_{1}} = \frac{1}{2} m v_{2}^{2} - \frac{G M m}{r_{2}}$

Conocidos r₁ y r₂ calculamos en este par de ecuaciones las incógnitas v₁ y v₂

$v_{1}^{2} = \frac{2 G M r_{2}}{r_{1} (r_{1} + r_{2})} v_{2}^{2} = \frac{2 G M r_{1}}{r_{2} (r_{1} + r_{2})}$

La energía de la nave espacial es constante en todos los puntos de la trayectoria e igual a

$E_{2} = \frac{1}{2} m v_{1}^{2} - \frac{G M m}{r_{1}}$

La energía que hemos de suministrar al satélite en la posición A para que pase de la órbita circular a la trayectoria de transferencia es la diferencia E₂-E₁ o bien,

$Δ E_{A} = \frac{1}{2} m v_{1}^{2} - \frac{1}{2} m v_{A}^{2} = \frac{G M m}{2 r_{1}} (\frac{r_{2} - r_{1}}{r_{2} + r_{1}})$

Órbita circular exterior

Una vez que la nave espacial llega al punto B, ha de cambiar su velocidad para seguir la trayectoria circular de radio r₂. De nuevo, aplicando la dinámica del movimiento circular uniforme tenemos.

$\frac{G M m}{r_{2}^{2}} = m \frac{v_{B}^{2}}{r_{2}} v_{B}^{2} = \frac{G M}{r_{2}}$

La energía E₃ de la nave espacial en la órbita circular final es

$E_{3} = \frac{1}{2} m v_{B}^{2} - \frac{G M m}{r_{2}} = - \frac{G M m}{2 r_{2}}$

La energía que hemos de suministrar al satélite para que pase de la órbita de transferencia elíptica a la órbita circular de radio r₂ es la diferencia E₃-E₂o bien,

$Δ E_{B} = \frac{1}{2} m v_{B}^{2} - \frac{1}{2} m v_{2}^{2} = \frac{G M m}{2 r_{2}} (\frac{r_{2} - r_{1}}{r_{2} + r_{1}})$

El tiempo que tarda la nave espacial en pasar del punto A al punto B principio y fin de la trayectoria de transferencia, es la mitad del periodo P.

$P^{2} = \frac{4 π^{2} a^{3}}{G M} a = \frac{r_{2} + r_{1}}{2}$

Siendo a el semieje mayor de la elipse.

Combustible gastado por la nave espacial

Supondremos que la nave espacial cambia de velocidad en los puntos A y B mediante sendos impulsos, de duración muy corta, por lo que no tendremos en cuenta la acción del peso.

Al estudiar la dinámica de un cohete, calculamos la cantidad de combustible m₀-m que ha de gastar una nave espacial para incrementar su velocidad en v-v₀

$v - v_{0} = u \ln \frac{m_{0}}{m} \frac{m_{0}}{m} = \exp (\frac{v - v_{0}}{u})$

donde u es la velocidad de escape de los gases al quemarse el combustible, m₀ es la masa inicial y m es la masa final y Δv=v-v₀ es la variación de velocidad.

En la posición A, la variación de la velocidad es v₁-v_A
En la posición B, la variación de la velocidad es v_B-v₂

Ejemplo

Para situar un satélite de comunicaciones en órbita geosíncrona a 35770 km de altura sobre la superficie terrestre se emplea un remolcador espacial. Sabiendo que inicialmente el remolcador describe una órbita circular a 350 km de altura, determinar

La velocidad que debe tener el remolcador en el punto A para transferirlo a la órbita elíptica de transición
La velocidad que es necesario proporcionarle en el punto B para transferirlo finalmente a la órbita geoestacionaria
Calcular la energía que es necesario suministrar a un satélite de masa m para transferirlo desde la órbita circular a baja altura hasta la órbita geoestacionaria

Datos

Masa de la Tierra, M=5.98·10²⁴ kg.
Constante de la gravitación universal, G=6.67·10^-11 Nm²/kg²
Radio de la Tierra, R=6370 km

En primer lugar, transformamos las alturas de las órbitas en distancias al centro de la Tierra, r_A=(350+6370)·1000 m, r_B=(35770+6370)·1000 m.

Calculamos la velocidad del satélite en la órbita circular de 350 km de altura, v_A =7704.22 m/s. La energía inicial es E₁=-29.68·10⁶·m J (m es la masa de la nave espacial)
Calculamos la velocidad que debe alcanzar v₁ =10118.5 m/s, para transferirlo a la órbita de transición y la velocidad del satélite al finalizar dicha órbita elíptica, v₂ =1613.6 m/s. La energía de la nave espacial es E₂=-8.16·10⁶·m J. El tiempo que tarda la nave espacial en describir la órbita de transferencia es de 18994.2 s.
Calculamos la velocidad del satélite en la órbita geoestacionaria, v_B =3076.6 m/s. La energía de la nave espacial es esta órbita es E₃=-4.73·10⁶·m J

La variación de energía cinética ΔE_A, es la energía que debemos suministrar al satélite para que pase de la órbita circular de baja altura a la órbita elíptica de transición, ΔE_A=21.5 10⁶ m J.
La variación de energía cinética ΔE_B, es la energía que debemos suministrar al satélite para que pase de la órbita elíptica de transición a la órbita circular de mayor altura, ΔE_B=3.43 10⁶ m J.
La energía total que tenemos que suministrar al satélite será la suma de ambas cantidades ΔE=ΔE_A+ΔE_B =24.9 10⁶ m J.
La variación de velocidad del satélite para que pase de la órbita circular de radio r_A a la órbita de trasferencia es Δv_A=v₁-v_A=2414.3 m/s
La variación de velocidad del satélite para que pase de la órbita de trasnferencia a la órbita circular de radio r_B es Δv_B=v_B-v₂=1463 m/s
El tiempo de viaje, medio periodo, P/2 es de 5.3 h

M=5.98e24; %masa de la Tierr1
G=6.67e-11; %constante G
R=6.37e6; %radio de la Tierra
r2=35570*1000+R; %órbita exterior (35570 km de altura)
r1=350*1000+R;  %órbita interior  (350 km de altura)

vA=sqrt(G*M/r1); %velocidad en la órbita circular interior
vB=sqrt(G*M/r2); %velocidad en la órbita circular exterior

%velocidad de salida de la órbita interior
v1=sqrt(2*G*M*r2/(r1*(r1+r2)));
%energía que hay que proporcionar para pasar de vA a v1
inc_A=v1^2/2-vA^2/2; 
%velocidad de llegada a la órbita exterior
v2=r1*v1/r2; 
%energía que hay que proporcionar para pasar de v2 a vB
inc_B=vB^2/2-v2^2/2; 
fprintf('Velcidades en las órbitas circulares: vA: %5.1f, vB: %5.1f\n',vA,vB);
fprintf('órbita de transferencia v1: %5.1f, v2: %5.1f\n',v1,v2);
fprintf('Energía suministrada %7.1f \n',inc_A+inc_B);

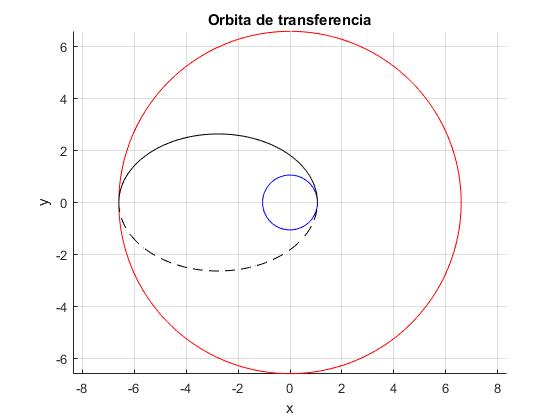
hold on
fplot(@(x) (r1/R)*cos(x), @(x) (r1/R)*sin(x),[0,2*pi],'color','b')
fplot(@(x) (r2/R)*cos(x), @(x) (r2/R)*sin(x),[0,2*pi],'color','r')
%órbita elíptica
a=(r1+r2)/2; %semieje mayor
ex=1-r1/a; %excentricidad
d=a*(1-ex^2);
r=@(x) (d/R)./(1+ex*cos(x));
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0,2*pi],'lineStyle','--','color','k') 
fplot(@(x) r(x).*cos(x), @(x) r(x).*sin(x),[0,pi],'color','k') 
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Orbita de tr1nsferencia')
%tiempo de viaje
P=pi*sqrt(a^3/(G*M));  %medio periodo
fprintf('Tiempo (h) %2.1f \n',P/3600);

Velcidades en las órbitas circulares: vA: 7704.2, vB: 3083.9
órbita de transferencia v1: 10115.1, v2: 1620.7
Energía suministrada 24922331.9 
Tiempo (h) 5.2

Transferencia mediante una trayectoria parabólica

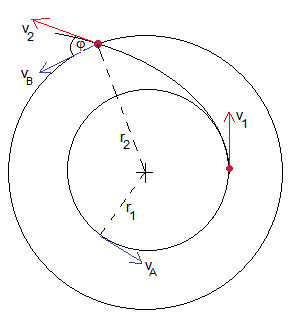
Consideremos una nave espacial en órbita circular de radio r₁ alrededor de un planeta de masa M. Los cohetes de la nave le proporcionan un impulso muy breve en la dirección de la velocidad de la nave, de modo que alcanza la velocidad de escape. La nave espacial seguirá una trayectoria parabólica tal como se muestra en la figura.

La ecuación de la dinámica del movimiento circular, nos proporciona la velocidad v_A de la nave espacial en su órbita circular de radio r₁.

$m \frac{v_{A}^{2}}{r_{1}} = \frac{G M m}{r_{1}^{2}} v_{A} = \sqrt{\frac{G M}{r_{1}}}$

La velocidad de escape v₁ es la mínima necesaria para que la nave llegue al infinito con velocidad nula. El principio de conservación de la energía se escribe

$\frac{1}{2} m v_{1}^{2} - \frac{G M m}{r_{1}} = 0 v_{1} = \sqrt{\frac{2 G M}{r_{1}}}$

El cambio de velocidad es

$Δ v_{A} = v_{1} - v_{A} = \sqrt{\frac{G M}{r_{1}}} (\sqrt{2} - 1)$

Se precisa otro impulso para que la nave espacial ingrese en una órbita circular de radio r₂. Cuando la nave espacial se encuentra a una distancia r₂ su velocidad ha disminuido

$\frac{1}{2} m v_{2}^{2} - \frac{G M m}{r_{2}} = 0 v_{2} = \sqrt{\frac{2 G M}{r_{2}}}$

El momento angular es constante a lo largo de la trayectoria parabólica r₁v₁=r₂v₂cosφ

Para que describa una órbita circular de radio r₂ su velocidad v_B es

$m \frac{v_{B}^{2}}{r_{2}} = \frac{G M m}{r_{2}^{2}} v_{B} = \sqrt{\frac{G M}{r_{2}}}$

La velocidad de la nave espacial para ingresar en la órbita circular de radio r₂ desde la trayectoria parabólica deberá cambiar tanto en módulo como en dirección (un ángulo φ)

$\vec{Δ v_{B}} = \vec{v_{B}} - \vec{v_{2}}$

Su módulo vale

$\begin{array}{l} Δ v_{B}^{2} = v_{B}^{2} + v_{2}^{2} - 2 v_{B} v_{2} \cos φ \\ Δ v_{B}^{2} = v_{B}^{2} + v_{2}^{2} - 2 v_{B} v_{2} \frac{r_{1} v_{1}}{r_{2} v_{2}} \\ Δ v_{B}^{2} = \frac{G M}{r_{2}} + \frac{2 G M}{r_{2}} - 2 \sqrt{\frac{r_{1}}{r_{2}}} \sqrt{\frac{G M}{r_{2}}} \sqrt{\frac{2 G M}{r_{2}}} \\ Δ v_{B} = \sqrt{\frac{G M}{r_{2}} (3 - 2 \sqrt{2} \sqrt{\frac{r_{1}}{r_{2}}})} \end{array}$

Tiempo de viaje

En la página titulada Trayectorias parabólicas estudiamos la trayectoria parabólica y el tiempo t que tarda la nave espacial en desplazarse un ángulo θ a lo largo de dicha trayectoria

$t = \sqrt{\frac{2 r_{1}^{3}}{G M}} (\tan \frac{θ}{2} + \frac{\tan^{3} (θ / 2)}{3})$

r₁ es la distancia más cercana al planeta.

Como la ecuación de la trayectoria es

$r = \frac{d}{1 + \cos θ}$

Para θ=0, r₁=d/2. La intersección de la parábola con la circunferencia de radio r₂ nos da el ángulo θ

$r_{2} = \frac{2 r_{1}}{1 + \cos θ}$

Ejemplo

Volvemos al ejemplo estudiado en el apartado anterior, se trata de transferir un satélite artificial desde una órbita circular de baja altura, 350 km a una órbita geoestacionaria de 35770 km de altura

Con los datos

Masa de la Tierra, M=5.98·10²⁴ kg.
Constante de la gravitación universal, G=6.67·10^-11 Nm²/kg²
Radio de la Tierra, R=6370 km

Transformamos las alturas de las órbitas en distancias al centro de la Tierra, r₁=(350+6370)·1000 m, r₂=(35770+6370)·1000 m.

La variación de velocidad del satélite para que pase de la órbita circular de radio r₁ a la trayectoria parabólica es Δv_A=v₁-v_A=3191.2 m/s
La variación de velocidad del satélite para que pase de la trayectoria parabólica a la órbita circular de radio r₂ es Δv_B=4214.7 m/s

Los impulsos que debe proporcionar el cohete para cambiar la velocidad son mucho mayores que en caso de la órbita de transferencia elíptica, aunque el tiempo t=2.15 h de viaje es menor

El script dibuja las órbitas circulares y la trayectoria parabólica.

M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
R=6.37e6; %radio de la Tierra
r2=35570*1000/R+1; %orbita exterior (35570 km de altura)
r1=350*1000/R+1;  %órbita interior  (350 km de altura)
hold on
fplot(@(x) r1*cos(x), @(x) r1*sin(x),[0,2*pi])
fplot(@(x) r2*cos(x), @(x) r2*sin(x),[0,2*pi])
th=acos(2*r1/r2-1);
ang=linspace(0,th,100);
x1=2*r1*cos(ang)./(1+cos(ang));
y1=2*r1*sin(ang)./(1+cos(ang));
plot(x1,y1,'k')
plot(r2*cos(th),r2*sin(th),'o','markersize',3,'markeredgecolor','r'
,'markerfacecolor','r')
hold off
axis equal
axis off

%tiempo de viaje
t=sqrt(2*(r1*R)^3/(G*M))*(tan(th/2)+tan(th/2)^3/3);
disp(t/3600)
%variaciones de velocidad
Dv_A=sqrt(G*M/(r1*R))*(sqrt(2)-1);
Dv_B=sqrt((G*M/(r2*R))*(3-2*sqrt(2)*sqrt(r1/r2)));
disp([Dv_A, Dv_B])

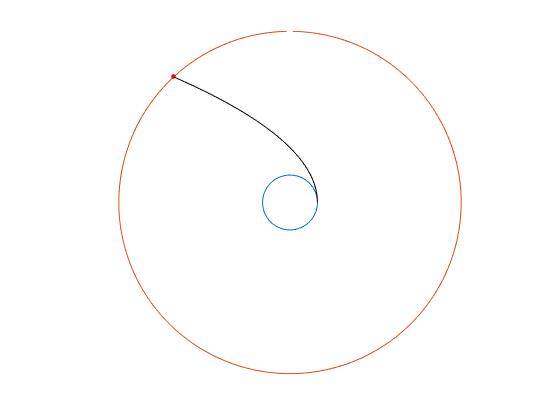
El tiempo t de viaje medido en horas y los cambios de velocidad en A y en B son

   2.1549
   1.0e+03 *    3.1912    4.2147

Transferencia mediante una trayectoria hiperbólica

Supongamos que a una nave espacial situada a 1000 km por encima de la Tierra se le proporciona una velocidad tangencial de v₁=12 km/s. Vamos a calcular la velocidad y el tiempo que tarda en llegar a la órbita de la Luna, r₂=384 000 km, despreciamos el efecto de la atracción de la Luna sobre la nave espacial.

La energía y el momento angular son

$\begin{array}{l} E = \frac{1}{2} m v_{1}^{2} - \frac{G M m}{r_{1}} \\ L = m r_{1} v_{1} \end{array}$

La ecuación de la trayectoria

$r = \frac{d}{1 + ε \cos θ} ε = \sqrt{1 + \frac{2 L^{2} E}{m^{3} G^{2} M^{2}}} d = \frac{L^{2}}{G M m^{2}}$

La intersección de la trayectoria hiperbólica con la órbita circular de la Luna de radio r₂ es

$r_{2} = \frac{d}{1 + ε \cos θ}, \cos θ = \frac{1}{ε} (\frac{d}{r_{2}} - 1)$

Dado el ángulo θ calculamos el tiempo t

$\begin{array}{l} \tanh (\frac{F}{2}) = \sqrt{\frac{ε - 1}{ε + 1}} \tan (\frac{θ}{2}) \\ ε \sinh F - F = {(ε^{2} - 1)}^{3 / 2} \frac{G^{2} M^{2} m^{3}}{L^{3}} t \end{array}$

M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
R=6.37e6; %radio de la Tierra
r2=384e6; %radio de la Luna
r1=1e6+R;  %órbita interior  (1000 km de altura)
v1=12000; %velocidad de la nave
E=v1^2/2-G*M/r1;
L=r1*v1;
d=L^2/(G*M);
ex=sqrt(1+2*L^2*E/(G^2*M^2));
hold on
fplot(@(x) r1*cos(x), @(x) r1*sin(x),[0,2*pi])
fplot(@(x) r2*cos(x), @(x) r2*sin(x),[0,2*pi])
th=acos((d/r2-1)/ex);
ang=linspace(0,th,100);
x1=d*cos(ang)./(1+ex*cos(ang));
y1=d*sin(ang)./(1+ex*cos(ang));
plot(x1,y1,'k')
plot(r2*cos(th),r2*sin(th),'o','markersize',3,'markeredgecolor',
'r','markerfacecolor','r')
hold off
axis equal
axis off

%tiempo de viaje
F=2*atanh(sqrt((ex-1)/(ex+1))*tan(th/2));
t=(ex*sinh(F)-F)*L^3/((ex^2-1)^(3/2)*G^2*M^2);
disp(t/3600) %tiempo en horas

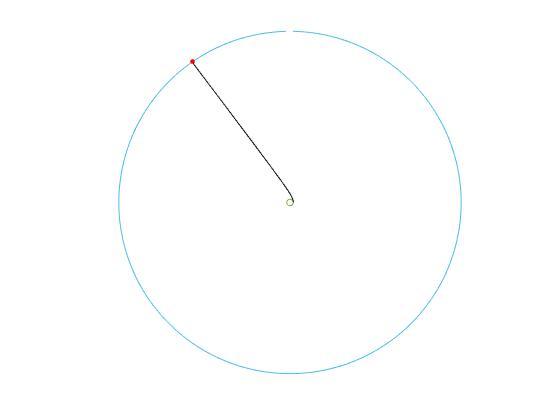
El tiempo de vuelo es t=16.39 horas

 16.3910

Las componentes de la velocidad de la nave espacial en el punto de intersección son

$\begin{array}{l} v_{θ} = r \frac{d θ}{d t} = \frac{L}{m r_{2}} \\ v_{r} = \frac{d r}{d t} = \sqrt{\frac{2}{m} (E - \frac{L^{2}}{2 m r_{2}^{2}} + \frac{G M m}{r_{2}})} \end{array}$

El ángulo que forma el vector velocidad con la dirección tangencial a la órbita circular de la Luna ess tanφ=v_r/v_θ

Para insertar la nave espacial en la órbita circular de la Luna, se tiene que cambiar tanto el módulo como la dirección de su velocidad

La velocidad de la Luna en su órbita circular alrededor de la Tierra es

$m \frac{v_{B}^{2}}{r_{2}} = \frac{G M m}{r_{2}^{2}}, v_{B} = \sqrt{\frac{G M}{r_{2}}}$

cuya dirección es tangente a la circunferencia de radio r₂

Añadimos líneas de código al script

...
%vector velocidad
v_th=L/r2;
v_r=sqrt(E-L^2/(2*r2^2)+G*M/r2);
v2=sqrt(v_r^2+v_th^2); %módulo de la velocidad
phi=atan(v_r/v_th); %dirección de la velocidad
vB=sqrt(G*M/r2); %velocidad de la Luna en su órbita circular
disp([v2,vB])

   1.0e+03 *    4.3526    1.0192

La velocidad de la nave espacial cuando llega a la órbita de la Luna es v₂=4352 m/s y la velocidad de la Luna en su órbita circular es v_B=1019 m/s.

Transferencia mediante órbita elíptica

Comparamos la transferencia mediante una trayectoria hiperbólica con la de una órbita elíptica cuyo perigeo es r₁ y apogeo r₂ (radio de la órbita circular de la Luna)

Calculamos la velocidad v₁ en el perigeo y v₂en el apogeo a partir de las ecuaciones de la energía y el momento angular

$\begin{array}{l} {\begin{cases} m r_{1} v_{1} = m r_{2} v_{2} \\ \frac{1}{2} m v_{1}^{2} - \frac{G M m}{r_{1}} = \frac{1}{2} m v_{1}^{2} - \frac{G M m}{r_{2}} \end{cases} \\ v_{1} = \sqrt{\frac{2 G M r_{2}}{r_{1} (r_{2} + r_{1})}}, v_{2} = \sqrt{\frac{2 G M r_{1}}{r_{2} (r_{2} + r_{1})}} \end{array}$

El tiempo que tarda la nave espacial en llegar a la órbita de la Luna desde las proximidades de la Tierra es medio periodo

$P^{2} = \frac{4 π^{2} a^{3}}{G M} a = \frac{r_{1} + r_{2}}{2}$

M=5.98e24; %masa de la Tierra
G=6.67e-11; %constante G
R=6.37e6; %radio de la Tierra
r2=384e6; %radio de la Luna
r1=1e6+R;  %órbita interior  (1000 km de altura)
v1=sqrt(2*G*M*r2/(r1*(r1+r2))); %velocidad perigeo
v2=sqrt(2*G*M*r1/(r2*(r1+r2))); %velocidad apogeo
E=v1^2/2-G*M/r1;
L=r1*v1;
d=L^2/(G*M);
ex=sqrt(1+2*L^2*E/(G^2*M^2));
hold on
fplot(@(x) r1*cos(x), @(x) r1*sin(x),[0,2*pi])
fplot(@(x) r2*cos(x), @(x) r2*sin(x),[0,2*pi])
fplot(@(x) d*cos(x)./(1+ex*cos(x)), @(x)  d*sin(x)./(1+ex*cos(x)),
[0,pi], 'color','k')

hold off
axis equal
axis off

%tiempo de viaje
t=pi*sqrt((r1+r2)^3/(8*G*M));
disp(t/3600) %tiempo en horas
vB=sqrt(G*M/r2); %velocidad de la Luna en su órbita circular
disp([v2,vB])

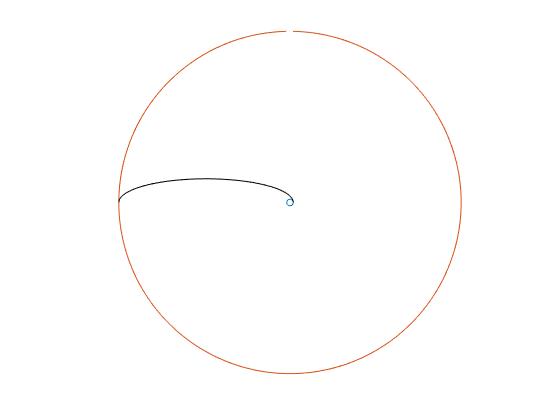
El tiempo de vuelo es t=119.6 horas, casi 5 días

119.6107

Añadimos líneas de código al script

...
vB=sqrt(G*M/r2); %velocidad de la Luna en su órbita circular
disp([v2,vB])

   1.0e+03 *    0.1978    1.0192

La nave espacial llega a la órbita de la Luna con velocidad v₂= 0.1978 km/s cuya dirección es tangente a la órbita circular de la Luna. Para insertar la nave en la órbita circular de la Luna, se tiene que cambiar el módulo de su velocidad a v_B=1.0192 km/s

Referencias

Lim Yun-kuo. Problems and solutions on Mechanics. World Scientific (1994). Problem 1063, pp. 94-97

Victor G. Szebehely, Hans Mark. Adventures in Celestial Mechanics. Wiley-VCH Verlag (2004), Problem 7.5, pp. 126-132