Intensidad de la radiación solar sobre una superficie plana inclinada
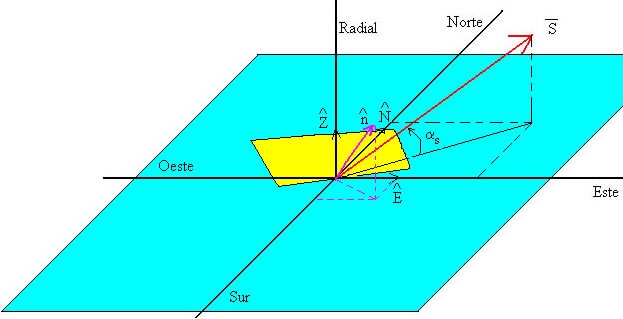
Se define la orientación del vector unitario perpendicular a la placa, del mismo modo que con el vector unitario . Forma un ángulo γ con la dirección Norte (positivo en el sentido de las agujas del reloj, hacia el Este), le llamaremos acimut de la placa. La placa inclinada forma un ángulo β con el plano horizontal ( ), el vector forma un ángulo de 90-β con el plano horizontal. El vector se expresa de forma similar al vector .
La intensidad de la radiación sobre la placa vale
I=I0·cosθ
Donde I0 es la intensidad incidente sobre una placa normal a la dirección de la luz solar, θ es el ánulo de incidencia de la radicación solar sobre la placa, es decir, el ángulo entre y . (véase la ley de la reflexión).
Efectuando el producto escalar entre estos dos vectores unitarios calculamos el coseno del ángulo θ.
Teniendo en cuenta las tres relaciones encontradas en la página anterior:
cosαs·sinγs=-sinω·cosδ
cosαs·cosγs=cosλ·sinδ-sinλ·cosω·cosδ
sinαs=cosλ·cosω·cosδ+sinλ·sinδ
Expresamos cosθ en términos de los ángulos δ (declinación), λ (latitud), ω (ángulo horario).
cosθ=-sinω·cosδ·sinβ·sinγ+cosλ·sinδ·sinβ·cosγ-sinλ·cosω·cosδ·sinβ·cosγ+cosλ·cosδ·cosω·cosβ+sinλ·sinδ·cosβ
Ejemplo: Una placa inclinada 45° apunta 10° hacia el sur-oeste y está situada en un punto de latitud 35°N. Calcular el ángulo incidente θ 2h después del mediodía el 15 de junio.
Datos: latitud λ=35°, ángulo horario, ω=30°, orientación de la placa γ=190°, ángulo de inclinación de la placa β=45°
Según hemos visto, la declinación solar δ se calcula mediante la siguiente fórmula
δ=0.006918-0.399912·cos(x)+0.070257·sin(x)-0.006758·cos(2x)+0.000907·sin(2x)-0.002697·cos(3x)
+0.001480·sin(3x).
Declinación el 15 de junio, N=15+151=166, h=14 (Día 166, hora 14) por lo que δ=23.28°
Poniendo todos los datos en la fórmula obtenemos cosθ=0.7698, que corresponde a un ángulo θ=39.67°
Escribimos un script para realizar este cálculo y otros similares
latitud=input('Latitud: ');
inclina=input('Inclinación de la placa: ');
acimut=input('Orientación placa (0-360), 90° Este, 180° Sur: ');
N=input('Numero de día: ');
h=input('Hora (0-24), las 12 es mediodía: ');
x=2*pi*(N-1-(h-12)/24)/365;
delta=(0.006918-0.399912*cos(x)+0.070257*sin(x)-0.006758*cos(2*x)
+0.000907*sin(2*x)
-0.002697*cos(3*x)+0.001480*sin(3*x));
%convierte la hora en ángulo horario -180° son las 0 h,
%180° son las 24 h
w=(h-12)*pi/12;
gamma=acimut*pi/180;
lambda=latitud*pi/180;
beta=inclina*pi/180; %inclinación d ela placa
cos_ang=-sin(w)*cos(delta)*sin(beta)*sin(gamma)+
cos(lambda)*sin(beta)*sin(delta)*cos(gamma)
-sin(lambda)*cos(w)*cos(delta)*sin(beta)*cos(gamma)+
cos(lambda)*cos(delta)*cos(w)*cos(beta)
+sin(lambda)*sin(delta)*cos(beta);
fprintf('El coseno del ángulo es: %1.4f\n',cos_ang)
Latitud: 35 Inclinación de la placa: 45 Orientación placa (0-360), 90º Este, 180º Sur: 190 Numero de día: 166 Hora (0-24), las 12 es mediodía: 14 El coseno del ángulo es: 0.7698
Referencia
Sproul A. B. Derivation of solar geometric relationship using vector analysis. Renewable Energy. 32 (2007) 1187-1205.

