Dinámica del movimiento circular uniforme
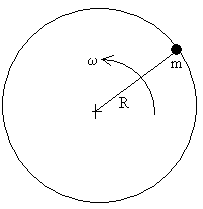
1.-Un pequeño bloque de 1 kg de masa está atado a una cuerda de 0.6 m, y gira a 60 r.p.m. describiendo una circunferencia vertical. Calcular la tensión de la cuerda cuando el bloque se encuentra:
- En el punto más alto de su trayectoria.
- En el más bajo de su trayectoria.
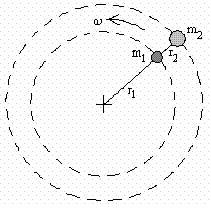
2.-Dos bloques de masas m1=2 kg y m2=3 kg unidos por una cuerda inextensible giran con la misma velocidad angular ω, describiendo dos trayectorias circulares situadas en el plano horizontal de radios r1=30 cm y r2=50 cm, respectivamente. Sabiendo que la tensión de la cuerda que une el centro de las trayectorias con el bloque de masa m1 es de 40 N. Calcular:
- La tensión de la cuerda que une ambas masas.
- La velocidad angular de giro ω.
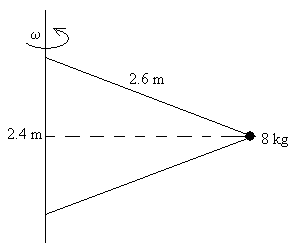
3.-Un bloque de 8 kg está sujeto a una barra vertical mediante dos cuerdas. Cuando el sistema gira alrededor del eje de la barra las cuerdas están tensadas, según se muestra en la figura.
- ¿Cuántas revoluciones por minuto ha de dar el sistema para que la tensión de la cuerda superior sea de 250 N?
- ¿Cuál es entonces la tensión de la cuerda inferior?
4.-Un vehículo de 750 kg toma una curva helada (sin rozamiento) de 160 m de radio a 90 km/h. ¿Cuál debe ser el ángulo del peralte para que el vehículo se mantenga en la curva (sin salirse)?
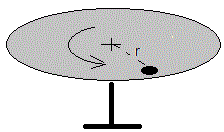
5.-Se coloca una moneda de masa m a una distancia r del centro de un disco que gira con velocidad angular ω. Si el coeficiente estático de rozamiento entre la superficie de la moneda y del disco es μs.
- Determinar la máxima velocidad angular a la que puede girar el disco para que la moneda no se caiga.
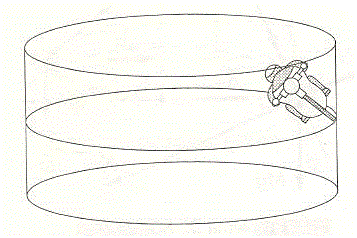
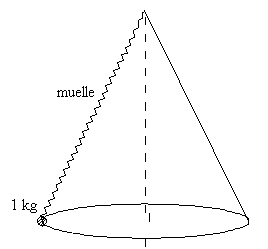
6.-Calcular la velocidad mínima que tiene que tener el motorista (considerado como una masa puntual) que trabaja en 'el tubo de la muerte' (aparato de atracción de feria representada en la figura) para que no se caiga. Diámetro del tubo: 10 m. Coeficiente estático de rozamiento entre las ruedas de la motocicleta y la pared: 0.5.
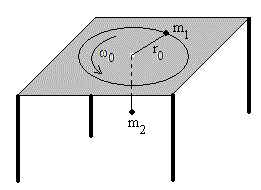
7.-La masa m1 describe una trayectoria circular de radio r0 sobre una mesa horizontal sin rozamiento. Está sujeta a una cuerda que pasa a través de un orificio (sin rozamiento) situado en el centro de la mesa. Una segunda masa m2 está sujeta en el otro extremo de la cuerda.
- Determinar la velocidad angular de rotación ω0 función de m1, m2 y r0
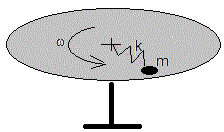
8.-Una partícula de masa m está unida a un muelle de constante k y longitud r0 sin deformar. Se coloca sobre una plataforma en rotación, que gira con velocidad angular constante ω, con un extremo del muelle unido al eje.
- ¿Cuál es la longitud r+r0 del muelle deformado?
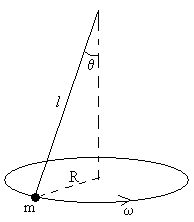
9.-Una partícula atada a una cuerda de 50 cm de longitud gira como un péndulo cónico, como muestra la figura. Calcular
- La velocidad angular de rotación de la masa puntual para que el ángulo que forma la cuerda con la vertical sea de 60º
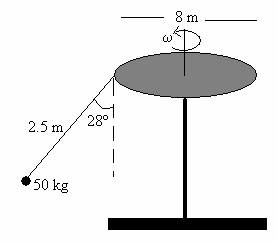
10.-Un juego de un parque de atracciones consta de una plataforma circular de 8 m de diámetro que gira. De la plataforma cuelgan “sillas voladoras” suspendidas de unas cadenas de 2.5 m de longitud. Cuando la plataforma gira las cadenas que sostienen los asientos forman un ángulo de 28º con la vertical.
- ¿Cuál es la velocidad angular de rotación?
- Si la masa del asiento y del niño es de 50 kg. ¿Cuál es la tensión de la cadena?.
11.-Enganchamos una partícula de 1 kg a un resorte de masa despreciable cuya longitud natural es de 48 cm y la constante recuperadora 10 N/cm. Lo hacemos girar como un péndulo cónico con una velocidad angular constante de 60 r.p.m. Calcular:
- El alargamiento del resorte.
- El ángulo que forma la altura del cono con la generatriz.
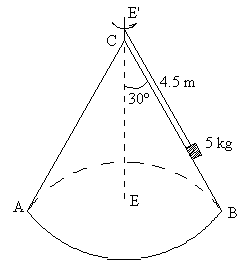
12.-Un cuerpo de 5 kg de masa se encuentra sobre una superficie cónica lisa ABC, y está girando alrededor del eje EE' con una velocidad angular de 10 r.p.m. Calcular:
- La reacción de la superficie cónica.
- La tensión de la cuerda.
- La velocidad angular a la que ha de girar el cuerpo para anular la reacción de la superficie cónica.
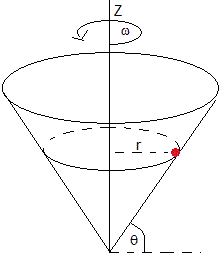
13.-Una partícula de masa m se coloca en el interior de una superficie cónica que forma un ángulo θ con la horizontal tal como se muestra en la figura.
Se hace girar el cono alrededor de su eje Z con velocidad angular ω. La partícula describe una circunferencia centrada en el eje de rotación de radio r.
Si el coeficiente estático de rozamiento entre la partícula y la superficie cónica es μ. Calcular la máxima y mínima velocidad angular para las cuales el bloque no se moverá.

 Solución
Solución