Dinámica de la partícula (II)
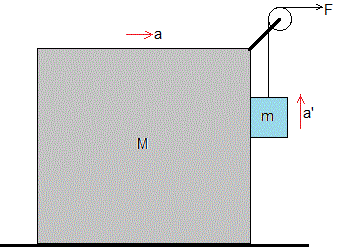
27.- El cuerpo de masa m desliza verticalmente hacia arriba con aceleración a' , el coeficiente cinético es μ .
El cuerpo de masa M desliza sobre el plano horizontal con aceleración a , el coeficiente cinético es también μ
Conocida la aceleración a , calcular la fuerza F
Physics Challenge for Teachers and Students. Up and away... Phys. Teach. 57, September (2019), pp. 501
Solución
Las ecuaciones del movimiento de cada uno de los dos cuerpos: componente horizontal y componente vertical, son
Cuerpo de masa m
{
N
1
= m a
F − m g − μ
N
1
= m a '
Cuerpo de masa M
{
F −
N
1
− μ
N
2
= M a
N
2
− M g + μ
N
1
− F = 0
Las dos primeras ecuaciones nos dan la aceleración a'
F − m g − μ (
m a
) = m a '
a ' =
F
m
− g − μ a
De la primera, tercera y cuarta ecuación obtenemos la fuerza F conocida la aceleración a
N
2
= M g + F − μ (
m a
)
F −
N
1
− μ
N
2
= M a
F − (
m a
) − μ (
M g + F − μ (
m a
)
) = M a
F =
(
M + m −
μ
2
m
) a + μ M g
1 − μ
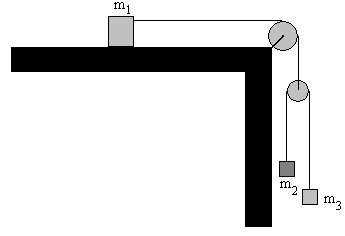
28.- Calcular la aceleración de los cuerpos m1 , m2 y m3 de la figura.
Solución
Ecuaciones del movimiento
{
T =
m
1
a
m
2
g −
T
2
=
m
2
( a − a ' )
m
3
g −
T
2
=
m
3
( a + a ' )
a =
4
m
2
m
3
4
m
2
m
3
+
m
1
m
3
+
m
2
m
1
g a ' =
(
m
1
m
3
−
m
2
m
1
)
4
m
2
m
3
+
m
1
m
3
+
m
2
m
1
g
La aceleración de cada uno de los cuerpos es
a
1
= a =
4
m
2
m
3
4
m
2
m
3
+
m
1
m
3
+
m
2
m
1
g
a
2
= a − a ' =
4
m
2
m
3
−
m
1
m
3
+
m
2
m
1
4
m
2
m
3
+
m
1
m
3
+
m
2
m
1
g
a
3
= a + a ' =
4
m
2
m
3
+
m
1
m
3
−
m
2
m
1
4
m
2
m
3
+
m
1
m
3
+
m
2
m
1
g
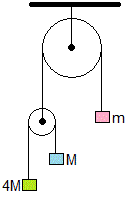
29.- En el sistema de la figura, las poleas y las cuerdas que unen los cuerpos tienen masas despreciables y no hay rozamiento. Calcular la aceleración de cada uno de los tres cuerpos.
Verificar que cuando los cuerpos se sueltan, alguno de ellos permanece en reposo para un determinado cociente m/M
Physics Challenge for Teachers and Students. M&m&4M . The Physics Teacher. Vol. 57, October 2019, pp. 567
Solución
Ecuaciones del movimiento
Cuerpo de masa m
T − m g = m a ,
a
1
= a
Polea
T = 2 T '
Cuerpo de masa M
T ' − M g = M (
a − a '
) ,
a
2
= a − a '
Cuerpo de masa 4M
4 M g − T ' = 4 M (
a + a '
) ,
a
3
= a + a '
Eliminando las tensiones T y T'
a =
8 M −
5
2
m
8 M +
5
2
m
g , a ' =
3 m
8 M +
5
2
m
g
{
a
1
= a =
8 M −
5
2
m
8 M +
5
2
m
g
a
2
= a − a ' =
8 M −
11
2
m
8 M +
5
2
m
g
a
3
= a + a ' =
8 M +
1
2
m
8 M +
5
2
m
g
El cuerpo de masa m permanecerá en reposo si a 1 =0, cuando m/M =16/5
El cuerpo de masa M permanecerá en reposo si a 2 =0, cuando m/M =16/11
La aceleración del cuerpo de masa 4M , a 3 >0
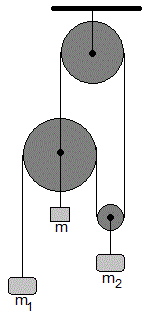
30.- Calcular las aceleraciones de los cuerpos de masa m 1 y m 2 . Sobre el eje de la polea izquierda cuelga un cuerpo de masa m .
Todas las poleas tienen masas despreciables, no hay rozamiento. Las cuerdas son inextensibles y de masa despreciable.
Physics Challenge for Teachers and Students. Tackle this! . The Physics Teacher. Vol. 59, October 2021 pp. 583
Solución
Como las poleas no tienen masa y no hay rozamiento, las tensiones en las distintas porciones de la cuerda son las mismas e iguales a T , tal como se indica con las flechas rojas de la figura.
Las ecuaciones del movimiento los cuerpos son
m
d
2
y
0
d
t
2
= m g + 2 T − T
m
1
d
2
y
1
d
t
2
=
m
1
g − T
m
2
d
2
y
2
d
t
2
=
m
2
g − 2 T
} {
d
2
y
0
d
t
2
= g +
T
m
d
2
y
1
d
t
2
= g −
T
m
1
d
2
y
2
d
t
2
= g − 2
T
m
2
La suma de las porciones de cuerda, más las enrolladas en las poleas πr es la longitud total de la cuerda que es constante
(y 1 -y 0 )+y 0 +(y 2 -y 0 )+y 2 =y 1 +2y 2 -y 0 =cte
La relación entre aceleraciones es
d
2
y
0
d
t
2
=
d
2
y
1
d
t
2
+ 2
d
2
y
2
d
t
2
T =
2 g
1
m
+
1
m
1
+
4
m
2
=
2 m
m
1
m
2
m
1
m
2
+ m
m
2
+ 4 m
m
1
g
Las aceleraciones de los cuerpos de masa m , m 1 y m 2 son
d
2
y
0
d
t
2
=
3
m
1
m
2
+ m
m
2
+ 4 m
m
1
m
1
m
2
+ m
m
2
+ 4 m
m
1
g
d
2
y
1
d
t
2
=
m
1
m
2
− m
m
2
+ 4 m
m
1
m
1
m
2
+ m
m
2
+ 4 m
m
1
g
d
2
y
2
d
t
2
=
m
1
m
2
+ m
m
2
m
1
m
2
+ m
m
2
+ 4 m
m
1
g
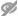Solución
