Dinámica de la partícula

Leyes de Newton

Ley de inercia. Una partícula libre o aislada se mueve con vector velocidad constante $\vec{v} = cte$ , o en movimiento rectilíneo y uniforme.
Definición de fuerza. $\vec{F} = \frac{d \vec{p}}{d t} \vec{p} = m \vec{v}$ . Si la masa m es constante $\vec{F} = m \vec{a}$
Principio de acción y reacción. Cuando dos partículas interactúan, la fuerza que ejerce una partícula sobre la otra es igual y de sentido contrario a la que ejerce la segunda sobre la primera.

Composición y descomposición de fuerzas

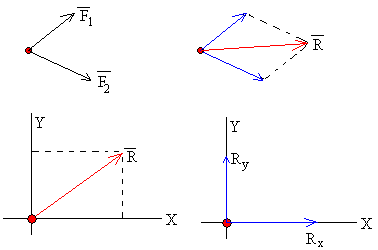
La acción simultánea de varias fuerzas concurrentes es igual a la acción de su resultante

La acción simulatánea de $\vec{F_{1}}$ y $\vec{F_{2}}$ es equivalente a la acción de su resultante (suma vectorial) $\vec{R} = \vec{F_{1}} + \vec{F_{2}}$
La acción de $\vec{R}$ es equivalente a la acción simultánea de sus componentes rectangulares R_x y R_y. $\vec{R} = R_{x} \hat{i} + R_{y} \hat{j}$

Fuerza de rozamiento

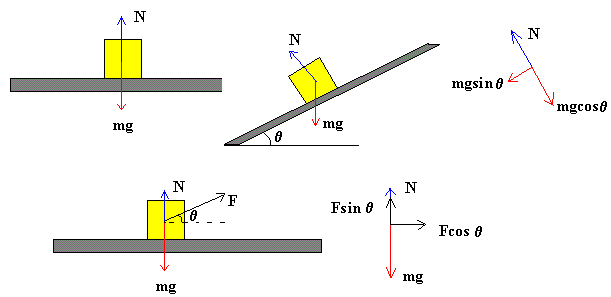
La fuerza normal, depende del peso del bloque, la inclinación del plano y de las otras fuerzas que se ejerzan sobre el bloque

La fuerza de rozamiento se opone al movimiento de un bloque que desliza sobre un plano.
El valor de la fuerza de rozamiento es en general desconocido, depende de las otras fuerzas que se ejerzan sobre el bloque
Cuando un cuerpo desliza, la fuerza de rozamiento es independiente de la velocidad y vale μ_kN
El máximo valor de la fuerza de rozamiento μ_sN, se alcanza cuando el bloque empieza a deslizar

Dinámica del movimiento circular uniforme

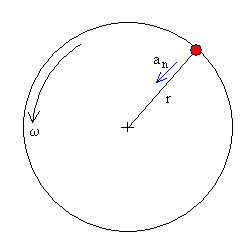
Una partícula describe un movimiento circular de radio r con velocidad angular constante ω, o con velocidad constante v=ω·r.

La resultante de las fuerzas que actúan sobre la partícula es igual al producto de la masa por la aceleración normal a_n=ω²·r=v²/r.

La aceleración normal a_n tiene dirección radial y apunta hacia el centro de la circunferencia.

Impulso

Consideremos el movimiento en una dimensión

La definición de fuerza es

$F = \frac{d p}{d t}$

Si la masa es constante, integrando

$m v - m v_{0} = \int_{t_{0}}^{t} F \cdot d t$

Momento de una fuerza

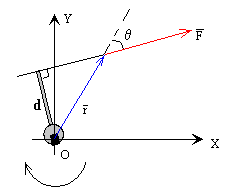
Se denomina momento de una fuerza respecto de un punto, al producto vectorial del vector posición $\vec{r}$ de la fuerza por el vector fuerza $\vec{F}$ .

$\vec{M} = \vec{r} \times \vec{F}$

El vector $\vec{M}$ tiene

Por módulo, M=F·r·sinθ=F·d. Siendo del brazo de la fuerza (la distancia desde el punto O a la dirección de la fuerza)
Dirección, perpendicular al plano determinado por la fuerza $\vec{F}$ de la fuerza por el vector fuerza $\vec{F}$ y el punto O.
Sentido, la aplicación de la regla del sacacorchos

La analogía de la llave y el tornillo, nos ayuda a entender el significado físico de la magnitud momento y a determinar correctamente el módulo, la dirección y el sentido del momento de una fuerza:

El módulo es el producto de la fuerza F por la longitud d de la llave. M=F·r·sinθ=F·d
La dirección, es la del eje del tornillo, eje Z
El sentido viene determinado por el avance del tornillo (hacia dentro, negativo) cuando hacemos girar a la llave.

Momento angular

Se define momento angular $\vec{L}$ respecto de un punto O como el vector producto vectorial

$\vec{L} = \vec{r} \times \vec{p} = \vec{r} \times m \vec{v}$

(la dirección del vector velocidad $\vec{v}$ es tangente a la trayectoria)

El cálculo del momento angular es similar al del momento de una fuerza respecto de un punto, sutituyendo el vector fuerza por el vector momento lineal.

Trabajo

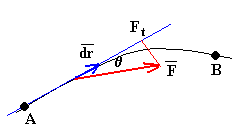
Se denomina trabajo infinitesimal, al producto escalar del vector fuerza por el vector desplazamiento.

$d W = \vec{F} \cdot \vec{d r} = F d s \cos θ = F_{t} d s$

Donde F_t es la componente de la fuerza a lo largo del desplazamiento, ds es el módulo del vector desplazamiento $\vec{d r}$ , y θ el ángulo que forma el vector fuerza con el vector desplazamiento.

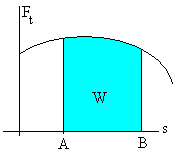
El trabajo total a lo largo de la trayectoria entre los puntos A y B es la suma de todos los trabajos infinitesimales

$W = \int_{A}^{B} \vec{F} \cdot \vec{d r} = \int_{A}^{B} F_{t} d s$

Su significado geométrico es el área bajo la representación gráfica de la función que relaciona la componente tangencial de la fuerza F_t, y el desplazamiento s.

Cuando la fuerza es constante, el trabajo es el producto del desplzamiento por la componente de la fuerza a lo largo del desplazamiento

W=F_t·s

Energía cinética

Si F es la resultante de las fuerzas que actúan sobre una partícula de masa m. El trabajo de dicha fuerza es igual a la diferencia entre el valor final y el valor inicial de la energía cinética de la partícula.

$W = \int_{A}^{B} F_{t} \cdot d s = \frac{1}{2} m v_{B}^{2} - \frac{1}{2} m v_{A}^{2}$

Fuerza conservativa. Energía potencial

Un fuerza es conservativa cuando el trabajo de dicha fuerza es igual a la diferencia entre los valores inicial y final de una función que solo depende de las coordenadas. A dicha función se le denomina energía potencial.

$\int_{A}^{B} \vec{F} \cdot \vec{d r} = E_{p A} - E_{p B} E_{p} = E_{p} (x, y, z)$

Denominación	Fuerza conservativa	Energía potencial
Peso	$\vec{F} = - m g \cdot \hat{j}$	E_p=mgy
Atracción gravitatoria	$\vec{F} = - G \frac{M m}{r^{2}} \hat{r}$	$E_{p} = - G \frac{M m}{r}$
Muelle elástico	$\vec{F} = - k x \cdot \hat{i}$	$E_{p} = \frac{1}{2} k x^{2}$

Principio de conservación de la energía

Si solamente actúan fuerzas conservativas sobre una partícula, se cumple

E_kA+E_pA=E_kB+E_pB

La energía mecánica de la partícula (suma de la energía potencial más cinética) es constante en todos los puntos de su trayectoria.

Trabajo-energía

En general, sobre una partícula actúan fuerzas conservativas $\vec{F_{c}}$ y no conservativas $\vec{F_{nc}}$

$\int_{A}^{B} \vec{F_{n c}} \cdot \vec{d r} = {(E_{k} + E_{p})}_{B} - {(E_{k} + E_{p})}_{A} = E_{B} - E_{A}$

El trabajo de una fuerza no conservativa modifica la energía mecánica (cinética más potencial) de la partícula.