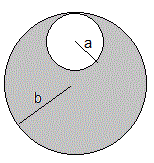
1.- Sea un pieza en forma de círculo de radio b al que le falta un círculo de radio a , tal como se muestra en la figura. La masa de la pieza es M . Calcular la posición de su centro de masas.
Solución
Situamos el origen en el centro del círculo de radio b y los ejes X e Y tal como se muestra en la figura
Por simetría, el centro de masas está en el eje Y, xcm =0
Sabiendo que la masa de la pieza es M , calculamos la masa ma del círculo de radio a y la masa mb del círculo de radio b
m
b
= M
π
b
2
π
b
2
− π
a
2
= M
b
2
b
2
−
a
2
m
a
= M
π
a
2
π
b
2
− π
a
2
= M
a
2
b
2
−
a
2
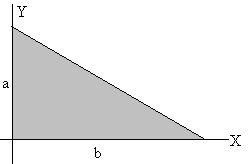
2.- Hallar la posición del c. m. del triángulo de la figura.
Solución
Ecuación de la recta (hipotenusa)
y = −
a
b
x + a
Elemento diferencial de área, dA=y·dx
x
c m
=
∫
x · d A
∫
d A
=
1
3
b
∫
x · d A
=
∫
x ( y · d x ) =
∫
0
b
x (
−
a
b
x + a
)
d x =
1
6
a
b
2
∫
d A
=
∫
y · d x =
∫
0
b
(
−
a
b
x + a
)
d x =
1
2
a b
Elemento diferencial de área, dA=x·dy
y
c m
=
∫
y · d A
∫
d A
=
1
3
a
∫
y · d A
=
∫
y ( x · d y ) =
∫
0
a
x (
−
b
a
y + b
)
d y =
1
6
a
2
b
∫
d A
=
∫
x · d y =
∫
0
a
(
−
b
a
x + b
)
d y =
1
2
a b
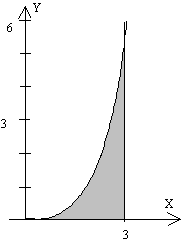
3.- Determinar la posición del centro de masa de la siguiente
figura plana y homogénea, formada por la región comprendida entre la parábola y =2x 2 /3
y el eje X, y la recta x =3.
Solución
Elemento diferencial de área, dA=y·dx
x
c m
=
∫
x · d A
∫
d A
=
9
4
∫
x · d A
=
∫
x ( y · d x ) =
∫
0
3
x
2
3
x
2
·
d x =
27
2
∫
d A
=
∫
y · d x =
∫
0
3
2
3
x
2
·
d x = 6
Elemento diferencial de área, dA= (3-x )·dy
y
c m
=
∫
y · d A
∫
d A
=
9
5
∫
y · d A
=
∫
y ( 3 − x ) · d y =
∫
0
3
2
3
x
2
( 3 − x )
4
3
x · d x =
54
5
∫
d A
=
∫
( 3 − x ) · d y =
∫
0
3
( 3 − x
)
4
3
x · d x = 6
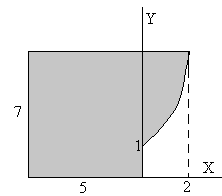
4.- Determinar la posición del centro de masa de la pieza
plana homogénea de la figura. La parte curva corresponde a la porción de
parábola y =3x 2 /2+1.
Solución
Centro de masa del rectángulo de área 35, x1 =-%/2, y1 =7/2
Centro de masa de la parte curva
Elemento diferencial de área, dA= (7-y )·dx
x
c m
=
∫
x · d A
∫
d A
=
3
4
∫
x · d A
=
∫
x ( 7 − y ) · d x =
∫
0
2
x (
7 −
3
2
x
2
− 1
) ·
d x = 6
∫
d A
=
∫
( 7 − y ) · d x =
∫
0
2
(
7 −
3
2
x
2
− 1
) ·
d x = 8
Elemento diferencial de área, dA=x·dy
y
c m
=
∫
y · d A
∫
d A
=
23
5
∫
y · d A
=
∫
y x · d y =
∫
0
2
(
3
2
x
2
+ 1
) x
( 3 x · d x ) =
184
5
∫
d A
=
∫
x · d y =
∫
0
2
x ( 3 x · d x )
= 8
Centro de masas de las dos figuras
x
c m
=
35 (
−
5
2
) + 8 (
3
4
)
35 + 8
= −
163
86
y
c m
=
35 (
7
2
) + 8 (
23
5
)
35 + 8
=
1593
430
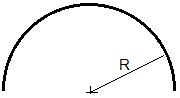
5.- Calcular el centro de masa de un alambre doblada en forma de semicircunferencia de radio R .
Solución
Situamos el origen en el centro de la semicircunferencia y los ejes X e Y tal como se muestra en la figura
Por simetría el centro de masas estará en el eje Y, xcm =0
Sea λ la densidad lineal (masa por unidad de longitud) del alambre. Consideremos un arco infinitesimal ds=R·dθ , marcado en color rojo en la figura. Su masa es dm=λ·ds=λR·dθ
y
c m
=
∫
y d m
∫
d m
=
∫
0
π
( R sin θ ) ( λ R · d θ )
∫
0
π
( λ R · d θ )
=
λ
R
2
∫
0
π
sin θ · d θ
λ R
∫
0
π
d θ
=
2 R
π
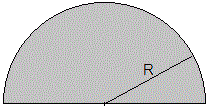
6.- Calcular el centro de masa de una placa en forma semicircular de radio R .
Solución
Situamos el origen en el centro de la semicircunferencia y los ejes X e Y tal como se muestra en la figura
Por simetría el centro de masas estará en el eje Y, xcm =0
Sea σ la densidad superficial (masa por unidad de área) de la placa semicircular. Consideremos una franja, de anchura dy , y de longitud 2x paralela al eje X, marcada en color rojo en la figura. Su masa es dm=σ (2x·dy )
y
c m
=
∫
y d m
∫
d m
=
∫
0
R
y (
σ 2
R
2
−
y
2
d y
)
∫
0
R
σ 2
R
2
−
y
2
d y
=
σ
∫
0
R
(
R
2
−
y
2
) 2 y · d y
σ
1
2
π
R
2
=
2
3
R
3
1
2
π
R
2
=
4 R
3 π
La integral de numerador es inmediata, la del denominador es el área de un semicírculo, que se puede calcular, expresando y en coordenadas polares y=R sinθ , dy=R cosθ·dθ
∫
0
R
2
R
2
−
y
2
d y =
∫
0
π / 2
2
R
2
cos
2
θ · d θ =
R
2
∫
0
π / 2
(
1 + cos ( 2 θ )
) d θ =
1
2
π
R
2
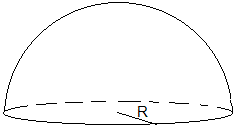
7.- Calcular el centro de masa de un cuerpo macizo en forma semiesférica de radio R .
Solución
Situamos el origen en el centro de la semiesfera y los ejes X e Y tal como se muestra en la figura
Por simetría el centro de masas estará en el eje Z, xcm =0, ycm =0
Sea ρ la densidad (masa por unidad de volumen) del cuerpo de forma semiesférica. Consideremos un cilindro de radio r y altura dz , paralelo al plano XY. Su masa es dm=ρ (πr 2 ·dz )
z
c m
=
∫
z d m
∫
d m
=
∫
0
R
z (
ρ π
r
2
d z
)
∫
0
R
ρ π
r
2
d z
Teniendo en cuenta que r 2 +z 2 =R 2
z
c m
=
ρ π
∫
0
R
z (
R
2
−
z
2
) d z
ρ π
∫
0
R
(
R
2
−
z
2
) d z
=
3 R
8
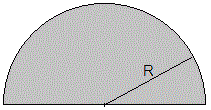
8.- Una pieza de forma semicircular de radio R , tiene una densidad σ que varía con el radio de la forma σ=cr 2 , donde r es la distancia desde el centro y c es una constante. Calcular la posición del centro de masas
Solución
Situamos el origen en el centro del semicírculo y los ejes X e Y tal como se muestra en la figura
Por simetría el centro de masas estará en el eje Y, xcm =0
Consideremos un elemento diferencial de radio r y de anchura dr , marcado en color rojo en la figura. El área de este elemento es πr·dr , y su masa dm=cr 2 (πr·dr )=πcr 3 dr . Su centro de masa se encuentra a una altura y =2r /π, (véase el problema 5 de esta página).
El centro de masa del semicírculo se encuentra en
y
c m
=
∫
0
R
2 r
π
(
c π
r
3
d r
)
∫
0
R
c π
r
3
d r
=
2 c
∫
0
R
r
4
d r
c π
∫
0
R
r
3
d r
=
8 R
5 π
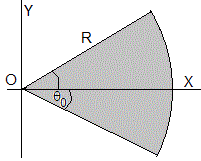
9.- Calcular la posición del centro de masa de una placa homogénea cuya forma es un sector circular de radio R y ángulo 2θ 0
Abhay Kumar Singh. Problems in Physics. New Age International Publishers, 2000, pp. 91-92
Solución
El eje X es un eje de simetría por lo que ycm =0, basta calcular la abscisa xcm del centro de masa
Dividimos el sector circular de ángulo 2θ 0 en sectores diferenciales de ángulo dθ (en color rosa), que podemos asimilar a triángulos isósceles de base R·dθ y altura R . El centro de masas de dichos triángulos se encuentra a 2R /3 del vértice.
Si ρ es la densidad constante de la placa, la masa dm de un sector diferencial es
d m = ρ (
1
2
(
R · d θ
) R
) =
1
2
ρ
R
2
d θ
La abscisa xcm es
x
c m
=
∫
−
θ
0
θ
0
x · d m
∫
−
θ
0
θ
0
d m
=
2
∫
0
θ
0
x · d m
∫
−
θ
0
θ
0
d m
=
ρ
R
2
∫
0
θ
0
(
2
3
R cos θ
) · d θ
1
2
ρ
R
2
∫
−
θ
0
θ
0
d θ
=
2
3
R sin θ
|
0
θ
0
θ
0
=
2
3
R
sin
θ
0
θ
0
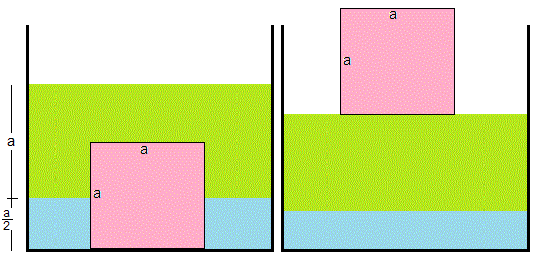
10.- Un cubo de densidad 2ρ , de lado a se coloca en el fondo de un recipiente de sección 3a 2 . El recipiente contiene dos líquidos inmiscibles, agua de densidad ρ y aceite de densidad 0.8ρ . La altura de agua es a /2 y la de aceite a .
Calcular el trabajo necesario para extraer el cubo del líquido (figura derecha).
Physics Challenge for Teachers and Students. Like oil and water! . The Physics Teacher. Vol. 54, February 2016. pp. 125
Solución
Volumen de agua (color azul) en el recipiente
V
A
= 3
a
2
a
2
−
a
2
a
2
=
a
3
El volumen de aceite (color verde) es la suma de dos partes B y C
V
a
=
V
B
+
V
C
= (
3
a
2
a
2
−
a
2
a
2
) + (
3
a
2
a
2
) =
a
3
+
3
2
a
3
=
5
2
a
3
Situación inicial
Los centros de masa se han señalado mediante puntos en la figura
Cuerpo altura del c.m masa energía potencial Cubo a /22ρa 3 ρa 4 g Agua A a /4ρa 3 ρa 4 g /4Aceite B a /4+a /2=3a /40.8ρa 3 0.6ρa 4 g Aceite C a +a /4=5a /41.2ρa 3 1.5ρa 4 g
La energía potencial inicial es Epi =(1+1/4+0.6+1.5)ρa 4 g =3.35ρa 4 g
Situación final
Al retirar el cubo las alturas h1 del aceite y h2 del agua cambia
h
2
=
a
3
3
a
2
=
1
3
a ,
h
1
=
5
2
a
3
3
a
2
=
5
6
a
Los centros de masa se han señalado mediante puntos en la figura
Cuerpo altura del c.m masa energía potencial Cubo h 1 +h 2 +a /2=5a /32ρa 3 10ρa 4 g /3 Aceite h 2 +h 1 /2=3a /42ρa 3 3ρa 4 g /2 Agua h 2 /2=a /6ρa 3 ρa 4 g /6
La energía potencial final es Epf =(10/3+3/2+1/6)ρa 4 g =5ρa 4 g
El trabajo es la diferencia entre las dos energías potenciales, W=Epf -Epi =(5-3.35) ρa 4 g =1.65ρa 4 g
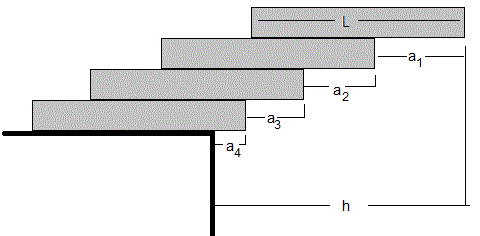
11.- Cuatro bloques homogéneos de masa m y longitud L idénticos se apilan unos encima de otros tal como se muestra en la figura.
Masatsugu Suzuki. Lecture Notes of General Physics I and II Calculus Based
Solución
Se sitúa un bloque homogéneo de masa m y longitud L sobe una mesa tal como se muestra en la figura. El bloque estará en equilibrio sobre la mesa siempre que d<L /2. Si d≥L /2 el bloque desliza sobre el borde y cae .
La máxima distancia d se obtiene cuando el la dirección del peso del bloque pasa por borde de la mesa
a 1 =L/2
El segundo bloque tiene encima el primero. El centro de masas del conjunto formado por estos dos bloques es
a
2
=
m
L
2
+ m · 0
2 m
=
L
4
El tercer bloque tiene encima el primero y el segundo. El centro de masas del conjunto formado por estos tres bloques es
a
3
=
m
L
2
+ 2 m · 0
3 m
=
L
6
El cuarto bloque tiene encima el primero, el segundo y el tercero. El centro de masas del conjunto formado por estos cuatro bloques es
a
4
=
m
L
2
+ 3 m · 0
4 m
=
L
8
y así...., sucesivamente
La máxima distancia h del extremo derecho del primer bloque al borde de la mesa es
h =
L
2
+
L
4
+
L
6
+
L
8
=
25
24
L
>> format rat
>> 1/2+1/4+1/6+1/8
ans = 25/24
>> syms k;
>> symsum(1/k,k,1,4)/2
ans =25/24
En general, para n bloques apilados uno encima del otro. La máxima distancia h al borde de la mesa es
h =
1
2
∑
k = 1
n
1
k

 Solución
Solución