Principio de conservación del momento angular

El principio de conservación del momento angular afirma que si el momento de las fuerzas exteriores es cero (lo que no implica que las fuerzas exteriores sean cero, que sea un sistema aislado), el momento angular total se conserva, es decir, permanece constante.

${\displaystyle \frac{d\overrightarrow{L}}{dt}=\overrightarrow{M_{ext}}\overrightarrow{M_{ext}}=0\overrightarrow{L}=\text{cte}}$

Momento angular de una partícula

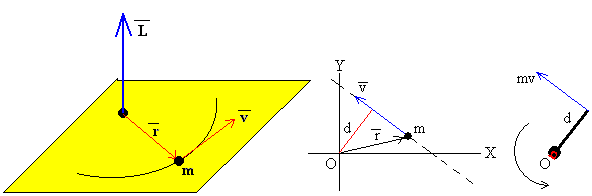
Momento angular de una partícula es el producto vectorial del vector posición $\overrightarrow{r}$ por el vector momento lineal $m\overrightarrow{v}$

${\displaystyle \overrightarrow{L}=\overrightarrow{r}\times m\overrightarrow{v}}$

• Se traza la dirección de la velocidad $\overrightarrow{v}$ y se dibuja y calcula la distancia d del origen O a dicha recta. El módulo del momento angular de la partícula es el producto L=mv·d.
• La dirección del momento angular es perpendicular al plano XY, es decir, el eje Z
• El sentido del momento angular se determina mediante la regla del sacacorchos, o de la analogía con la llave inglesa, la fuerza sobre el extremo de la llave está representada aquí por el momento lineal mv.

Momento angular de un sólido

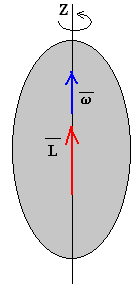
En general, el vector momento angular $\overrightarrow{L}$ no tiene la dirección del eje de rotación, es decir, el vector momento angular no coincide con su proyección L_z a lo largo del eje de rotación. Cuando coinciden se dice que el eje de rotación es un eje principal de inercia.

Para estos ejes existe una relación sencilla entre el momento angular y la velocidad angular, dos vectores que tienen la misma dirección, la del eje de rotación

${\displaystyle \overrightarrow{L}=I\overrightarrow{\omega }}$

Teorema de Steiner

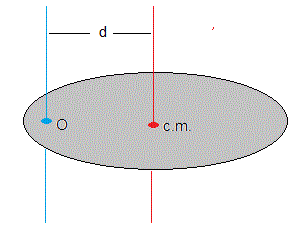
I_O=I_cm+Md²

I_O es el momento de inercia del sólido respecto de un eje que pasa por O

I_cm es el momento de inercia respecto de un eje paralelo que pasa por el centro de masas

d es la distancia entre los ejes paralelosy M la masa del sólido

Energía cinética de rotación

${\displaystyle E_k=\frac{1}{2}I{\omega }^2}$

I es el momento de inercia del sólido respecto del eje de rotación

ω es la velocidad angular de rotación

Ecuación de la dinámica de rotación

Iα=M

I es el momento de inercia del sólido respecto del eje de rotación

α es la aceleración angular de rotación

M es el momento de las fuerzas que actúan sobre el sólido rígido.

Trabajo y energía

El trabajo total cuando el sólido gira un ángulo θ es

${\displaystyle W={\displaystyle \underset{0}{\overset{\theta }{\int }}M·d\theta }=\frac{1}{2}I{\omega }^2-\frac{1}{2}I{\omega }_0^2}$

igual a la variación de energía cinética de rotación

Principio de conservación de la energía en el movimiento de rotación

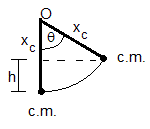
La fuerza conservativa peso actúa en el centro de masas de un sólido en rotación alrededor de un eje fijo.

La energía potencial se convierte en energía cinética de rotación y viceversa.

${\displaystyle mgh=\frac{1}{2}I{\omega }^2-\frac{1}{2}I{\omega }_0^2}$

h es la altura del cetro de masas, y x_c la distancia desde el eje de rotación y el centro de masas c.m. Como vemos en la figura h=x_c(1-cosθ)

Movimiento general de un sólido rígido

El movimiento general de un sólido rígido, es la composición de un movimiento de traslación del centro de masa y de un movimiento de rotación alrededor de un eje que pasa por el centro de masa. En el movimiento de rodar sin deslizar, la rueda se traslada a la vez que gira.

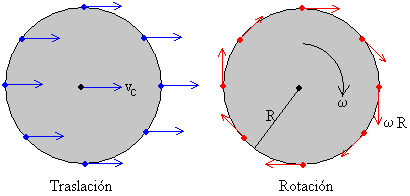
• En el movimiento de traslación, todos los puntos del sólido se mueven en trayectorias paralelas. La velocidad de un punto del sólido es la misma que la velocidad del centro de masas.

• En el movimiento de rotación alrededor de un eje que pasa por el centro de masas, la velocidad de un punto del sólido es proporcional la radio de la circunferencia que describe, su dirección es tangente a dicha circunferencia.

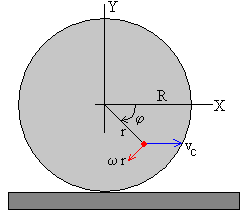
En el movimiento de rodar sin deslizar, existe una relación entre el movimiento de rotación y traslación. El punto de la rueda que está en contacto en un instante dado con el suelo tiene velocidad nula. Por tanto, se debe de cumplir que

v_c=ω R

La velocidad de traslación v_c es igual a la velocidad de rotación ω por el radio de la rueda R.

Sumando vectorialmente las dos velocidades podemos calcular la velocidad de cualquier punto P, que dista r del centro de una rueda de radio R, y que forma un ángulo φ, con la horizontal.

Ecuaciones del movimiento

• Movimiento de traslación del centro de masa

F=ma_c

F es la resultante de las fuerzas que actúan sobre el sólido

• Movimiento de rotación alrededor de un eje que pasa por el centro de masas

M=I_cα

M es el momento de las fuerzas que actúan sobre el sólido

Equilibrio

Sobre un sólido rígido actún varias fuerzas en distintos puntos, tal como se muestra en la figura

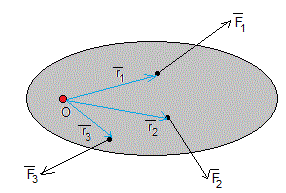
El sólido rígido se encuentra en equilibrio cuando

• La resultante de todas las fuerzas es nula
• El momento resultante respecto de cualquier punto O es nulo

${\displaystyle \begin{array}{l}{\displaystyle \sum _{i=1}^n\overrightarrow{F_i}=0}\\ {\displaystyle \sum _{i=1}^n\overrightarrow{r_i}\times \overrightarrow{F_i}=0}\end{array}}$

Centro de masas de una figura plana

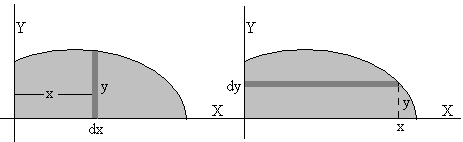
dA es elemento diferencial de área

${\displaystyle x_{cm}=\frac{{\displaystyle \int x·dA}}{{\displaystyle \int dA}}{y}_{cm}=\frac{{\displaystyle \int y·dA}}{{\displaystyle \int dA}}}$