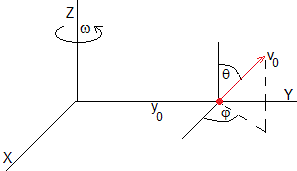
Se dispara un proyectil con velocidad inicial v₀ desde una plataforma en rotación con velocidad angular constante ω desde una posición situada a una distancia d al eje de rotación, formando un ángulo θ con el eje vertical y otro ángulo φ con la perpendicular a la línea que une el centro de la plataforma y la posición de disparo (eje X).

También podría describir el chorro de agua que sale de un aspersor, el dispositivo que al girar alrededor de su eje vertical distribuye agua sobre una superficie circular

En el caso del aspersor, hay una relación entre la velocidad angular de rotación ω y la velocidad inicial v₀, véase el artículo citado en las referencias

Sistema de referencia inercial

En el sistema inercial de referencia, el proyectil parte de la posición

${\displaystyle \{\begin{array}{l}{x}_0=0\\ y_0=d\\ z_0=0\end{array}}$

Con velocidad inicial

${\displaystyle \{\begin{array}{l}{v}_{0x}=v_0\sin \theta \cos \phi -\omega d\\ v_{0y}=v_0\sin \theta \sin \phi \\ v_{0z}=v_0\cos \theta \end{array}}$

El movimiento del proyectil es la composición de tres movimientos: uniformes a lo largo del eje X e Y y uniformemente acelerado a lo largo del eje Z

${\displaystyle \{\begin{array}{l}x=\left(v_0\sin \theta \cos \phi -\omega d\right)t\\ y=d+v_0\sin \theta \sin \phi ·t\\ z=v_0\cos \theta ·t-\frac{1}{2}g{t}^2\end{array}}$

Alcance

El proyectil retorna a la plataforma z=0, en el instante t_f

${\displaystyle t_f=\frac{2v_0\cos \theta }{g}}$

El alcance del proyectil es

${\displaystyle R^2=x^2(t_f)+y^2(t_f)={\left(v_0\sin \theta \cos \phi -\omega d\right)}^2{t}_f^2+{\left(d+v_0\sin \theta \sin \phi ·t_f\right)}^2}$

Elevamos al cuadrado ambos términos y simplificamos, teniendo en cuenta que sin²(ωt)+cos²(ωt)=1, llegamos al resultado

${\displaystyle R=\sqrt{v_0^2{\sin }^2\theta ·t_f^2+d^2\left({\omega }^2{t}_f^2+1\right)+2d{v}_0{t}_f\sin \theta \left(\sin \phi -\omega t_f\cos \phi \right)}}$

Sistema de referencia en rotación

En el sistema de referencia en rotación el eje Z' coincide con el eje Z que es el eje de rotación

La relación entre las aceleraciones $\overrightarrow{a\text{'}}$, en el sistema de referencia en rotación y $\overrightarrow{a}=-g\widehat{k}$, en el sistema de referencia inercial es

${\displaystyle \overrightarrow{a}=\overrightarrow{a\text{'}}+2\overrightarrow{\omega }\times \overrightarrow{v\text{'}}+\overrightarrow{\omega }\times \left(\overrightarrow{\omega }\times \overrightarrow{r}\right)}$

• $\overrightarrow{v\text{'}}$, es la velocidad en el sistema de referencia en rotación

• $\overrightarrow{r}$ , es la posición

• $\overrightarrow{\omega }=\omega \widehat{k}=\omega \widehat{k}\text{'}$ , es la velocidad angular de rotación

Los resultados de los productos vectoriales son

${\displaystyle \begin{array}{l}-2\overrightarrow{\omega }\times \overrightarrow{v}\text{'}=-2\left|\begin{array}{ccc}\widehat{i\text{'}}& \widehat{j}\text{'}& \widehat{k}\text{'}\\ 0& 0& \omega \\ \frac{dx\text{'}}{dt}& \frac{dy\text{'}}{dt}& \frac{dz\text{'}}{dt}\end{array}\right|=2\omega \frac{dy\text{'}}{dt}\widehat{i}\text{'}-2\omega \frac{dx\text{'}}{dt}\widehat{j}\text{'}\\ \overrightarrow{\omega }\times \overrightarrow{r}=\left|\begin{array}{ccc}\widehat{i}\text{'}& \widehat{j}\text{'}& \widehat{k}\text{'}\\ 0& 0& \omega \\ x\text{'}& y\text{'}& z\text{'}\end{array}\right|=-\omega y\text{'}\widehat{i}\text{'}+\omega x\text{'}\widehat{j}\text{'}\\ -\overrightarrow{\omega }\times \left(\overrightarrow{\omega }\times \overrightarrow{r}\right)=-\left|\begin{array}{ccc}\widehat{i}\text{'}& \widehat{j}\text{'}& \widehat{k}\text{'}\\ 0& 0& \omega \\ -\omega y\text{'}& \omega x\text{'}& 0\end{array}\right|={\omega }^{2}x\text{'}\widehat{i}\text{'}+{\omega }^{2}y\text{'}\widehat{j}\text{'}\\ \overrightarrow{a\text{'}}=-g\widehat{k}+\left(2\omega \frac{dy\text{'}}{dt}\widehat{i}\text{'}-2\omega \frac{dx\text{'}}{dt}\widehat{j}\text{'}\right)+\left({\omega }^{2}x\text{'}\widehat{i}\text{'}+{\omega }^{2}y\text{'}\widehat{j}\text{'}\right)\end{array}}$

Tenemos que resolver el sistema de tres ecuaciones diferenciales

${\displaystyle \begin{array}{l}\frac{d^{2}x\text{'}}{d{t}^2}-2\omega \frac{dy\text{'}}{dt}-{\omega }^{2}x\text{'}=0\\ \frac{d^{2}y\text{'}}{d{t}^2}+2\omega \frac{dx\text{'}}{dt}-{\omega }^{2}y\text{'}=0\\ \frac{d^{2}z\text{'}}{d{t}^2}=-g\end{array}}$

Con las condiciones iniciales, para t=0

${\displaystyle \begin{array}{l}\{\begin{array}{l}x{\text{'}}_0=0\\ y{\text{'}}_0=d\\ z{\text{'}}_0=0\end{array}\\ \{\begin{array}{l}v{\text{'}}_{0x}=v_0\sin \theta \cos \phi \\ v{\text{'}}_{0y}=v_0\sin \theta \sin \phi \\ v{\text{'}}_{0z}=v_0\cos \theta \end{array}\end{array}}$

La última ecuación diferencial es la más fácil de integrar, se trata de un movimiento rectilíneo uniformemente acelerado

${\displaystyle \begin{array}{l}\frac{dz\text{'}}{dt}=v_0\cos \theta -gt\\ z\text{'}=v_0\cos \theta ·t-\frac{1}{2}g{t}^2\end{array}}$

Para las dos primeras ecuaciones diferenciales, utilizamos notación compleja

${\displaystyle \begin{array}{l}\xi =x\text{'}+iy\text{'}\\ \frac{d^2\xi }{d{t}^2}-2\omega \left(\frac{dy\text{'}}{dt}-i\frac{dx\text{'}}{dt}\right)-{\omega }^2\xi =0\\ \frac{d^2\xi }{d{t}^2}+2\omega i\left(\frac{dx\text{'}}{dt}+i\frac{dy\text{'}}{dt}\right)-{\omega }^2\xi =0\\ \frac{d^2\xi }{d{t}^2}+2\omega i\frac{d\xi }{dt}-{\omega }^2\xi =0\end{array}}$

Las raíces de la ecuación característica son iguales

${\displaystyle s^2+2\omega is-{\omega }^2=\mathrm{0,}\{\begin{array}{l}{s}_1=-i\omega \\ s_2=-i\omega \end{array}}$

La solución de esta ecuación diferencial lineal con raíces repetidas es

${\displaystyle \begin{array}{l}\xi =C\exp \left(-i\omega t\right)+Dt\exp \left(-i\omega t\right)\\ \frac{d\xi }{dt}=-i\omega C\exp \left(-i\omega t\right)+D\exp \left(-i\omega t\right)-i\omega Dt\exp \left(-i\omega t\right)\end{array}}$

Donde C y D son coeficientes complejos cuya parte real e imaginaria se determinan a partir de las condiciones iniciales:

${\displaystyle t=0\{\begin{array}{l}\frac{dx\text{'}}{dt}=v{\text{'}}_{0x},\frac{dy\text{'}}{dt}=v{\text{'}}_{0y}\\ x\text{'}=\mathrm{0,}y\text{'}=d\end{array}}$

Los coeficientes valen

${\displaystyle \begin{array}{l}\{\begin{array}{l}id=C\\ v{\text{'}}_{0x}+iv{\text{'}}_{0y}=-i\omega C+D\end{array}\\ D=\left(v{\text{'}}_{0x}-\omega d\right)+iv{\text{'}}_{0y}\end{array}}$

Conocidas las componentes de la velocidad inicial, obtenemos la parte real x'(t) e imaginaria y'(t) de ξ

${\displaystyle \{\begin{array}{l}x\text{'}=\left(v_0\sin \theta \cos \phi -\omega d\right)t\cos (\omega t)+\left(d+v_0\sin \theta \sin \phi ·t\right)\sin (\omega t)\\ y\text{'}=-\left(v_0\sin \theta \cos \phi -\omega d\right)t\sin (\omega t)+\left(d+v_0\sin \theta \sin \phi ·t\right)\cos (\omega t)\end{array}}$

Alcance

El tiempo que tarda el proyectil en regresar a la plataforma z'=0

${\displaystyle t_f=\frac{2v_0\cos \theta }{g}}$

El alcance es

${\displaystyle \begin{array}{l}{R}^2=x{\text{'}}^2(t_f)+y{\text{'}}^2(t_f)={\left(v_0\sin \theta \cos \phi -\Omega d\right)}^2{t}_f^2+{\left(d+v_0\sin \theta \sin \phi ·t_f\right)}^2\\ R=\sqrt{v_0^2{\sin }^2\theta ·t_f^2+d^2\left({\Omega }^2{t}_f^2+1\right)+2d{v}_0{t}_f\sin \theta \left(\sin \phi -\Omega t_f\cos \phi \right)}\\ R=\sqrt{\frac{v_0^4{\sin }^2\left(2\theta \right)}{g^2}+d^2\left({\Omega }^2\frac{4v_0^2{\cos }^2\theta }{g^2}+1\right)+2d\frac{v_0^2\sin \left(2\theta \right)}{g}\left(\sin \phi -\Omega \frac{2v_0\cos \theta }{g}\cos \phi \right)}\end{array}}$

El mismo resultado se ha obtenido para el sistema de referencia inercial

Alcance máximo se obtiene

${\displaystyle \begin{array}{l}\frac{\partial R^2}{\partial \phi }=\mathrm{0,}\frac{\partial R^2}{\partial \theta }=0\\ \{\begin{array}{l}\cos \phi +\Omega \frac{2v_0\cos \theta }{g}\sin \phi =0\\ \frac{4v_0^4\sin \left(2\theta \right)\cos \left(2\theta \right)}{g^2}-d^2{\Omega }^2\frac{4v_0^{2}2\sin \theta \cos \theta }{g^2}+4d\frac{v_0^2\cos \left(2\theta \right)}{g}\left(\sin \phi -\Omega \frac{2v_0\cos \theta }{g}\cos \phi \right)+2d\frac{v_0^2\sin \left(2\theta \right)}{g}\left(\Omega \frac{2v_0\sin \theta }{g}\cos \phi \right)\end{array}\\ \{\begin{array}{l}\tan \phi =-\frac{g}{2\Omega v_0\cos \theta }\\ \frac{2v_0^4\sin \left(4\theta \right)}{g^2}-d^2{\Omega }^2\frac{4v_0^2\sin \left(2\theta \right)}{g^2}+4d\frac{v_0^2\cos \left(2\theta \right)}{g}\sin \phi +4d\Omega \frac{v_0^3}{g^2}\cos \phi \left(\sin \left(2\theta \right)\sin \theta -\cos \left(2\theta \right)\cos \theta \right)=0\end{array}\\ \{\begin{array}{l}\tan \phi =-\frac{g}{2\Omega v_0\cos \theta }\\ \frac{v_0^2\sin \left(4\theta \right)}{g}-\frac{2d^2{\Omega }^2\sin \left(2\theta \right)}{g}+2d{v}_0^2\cos \left(2\theta \right)\sin \phi +2d\Omega \frac{v_0}{g}\cos \phi \left(\sin \left(2\theta \right)\sin \theta -\cos \left(2\theta \right)\cos \theta \right)=0\end{array}\end{array}}$

Se resuelve este sistema de dos ecuaciones para obtener θ_m y φ_m que hacen que el alcance R sea máximo

Ejemplos

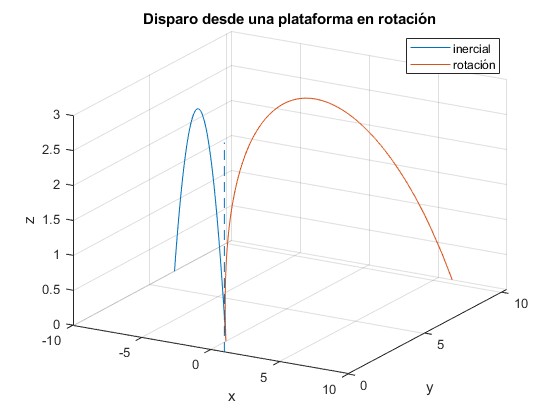
Representamos la trayectoria del proyectil en el sistema inercial de referencia y en el sistema de referencia en rotación para

• Velocidad angular de rotación, ω=5 rad/s
• Distancia al eje de rotación, d=1 m
• Velocidad inicial, v₀=10 m/s
• Angulos de tiro: con la vertical Z, θ=0, con el eje X, φ=0. (disparo vertical)

v0=10; %velocidad inicial
th=0; %ángulos de tiro 
phi=0;
d=1; %distancia al eje de rotación
w=5; %velocidad angular de rotación
tf=2*v0*cos(th)/9.8;%tiempo de regreso
%inercial
x=@(t) (v0*sin(th)*cos(phi)-w*d)*t; 
y=@(t) d+v0*sin(th)*sin(phi)*t;
z=@(t) v0*cos(th)*t-4.9*t.^2;
hold on
fplot3(x,y,z,[0,tf]);
%en rotación
X=@(t) (v0*sin(th)*cos(phi)-w*d)*t.*cos(w*t)+(d+v0*sin(th)*sin(phi)*t).*sin(w*t);
Y=@(t) -(v0*sin(th)*cos(phi)-w*d)*t.*sin(w*t)+(d+v0*sin(th)*sin(phi)*t).*cos(w*t);
fplot3(X,Y,z,[0,tf]);
line([d,d],[0,0],[0,3],'lineStyle','--')
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
legend('inercial','rotación','Location','best')
title('Disparo desde una plataforma en rotación')
view(30,25)

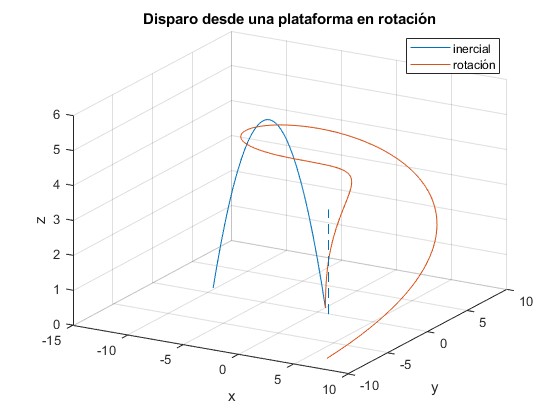
La línea a trazos señala ele eje Z de rotación

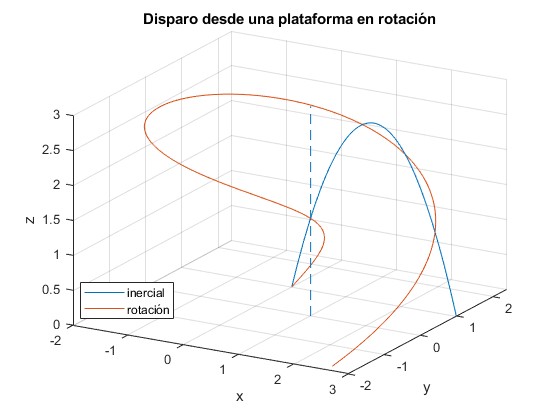
Cambiamos los ángulos de tiro, θ=π/4 (45°) y φ=0

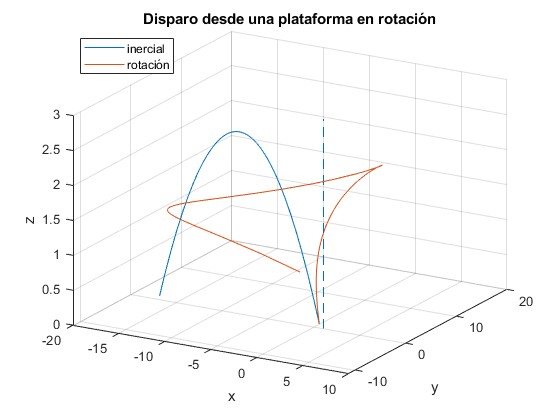
Cambiamos los ángulos de tiro, θ=π/4 (45°) y φ=π (180°)

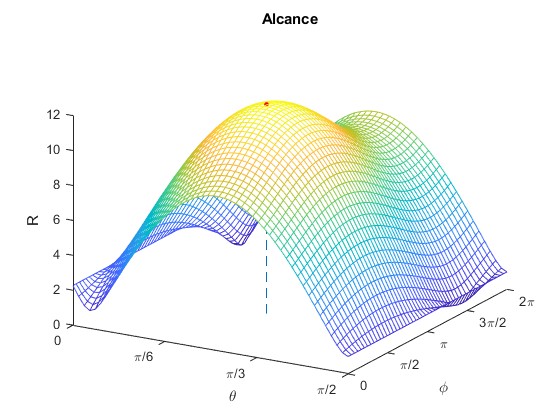
Representamos el alcance R en función de los ángulos de tiro θ y φ para la velocidad inicial v₀=10 m/s y una velocidad angular de rotación, ω=1 rad/s

Se señala mediante un punto de color rojo el alcance máximo

phi=linspace(0,2*pi,50);
th=linspace(0,pi/2,50);
v0=10; %velocidad inicial
w=1; %velocidad angular de rotación
[Th,Phi]=meshgrid(th,phi);
Z=sqrt(v0^4*sin(2*Th).^2/9.8^2+d^2*(4*w^2*v0^2*cos(Th).^2/9.8^2+1)+
2*d*v0^2*sin(2*Th).*(sin(Phi)-2*w*v0*cos(Th).*cos(Phi)/9.8)/9.8);
hold on
mesh(Th,Phi,Z);
set(gca,'XTick',0:pi/6:pi/2)
set(gca,'XTickLabel',{'0','\pi/6','\pi/3','\pi/2'})
set(gca,'YTick',0:pi/2:2*pi)
set(gca,'YTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})

g=@(th) atan(-4.9/(w*v0*cos(th)));
f=@(th) v0^2*sin(4*th)/9.8-2*d^2*w^2*sin(2*th)/9.8+2*d*v0^2*cos(2*th)*
sin(g(th))+2+d*w*v0*cos(g(th)*(sin(2*th)*sin(th)-cos(2*th)+cos(th)));
th_m=fzero(f,[0,pi/2]);
phi_m=pi+g(th_m);
R=@(th,phi) sqrt(v0^4*sin(2*th)^2/9.8^2+d^2*(4*w^2*v0^2*cos(th)^2/9.8^2+1)+
2*d*v0^2*sin(2*th)*(sin(phi)-2*w*v0*cos(th)*cos(phi)/9.8)/9.8);
R_m=R(th_m,phi_m);
plot3(th_m,phi_m, z_m,'ro','markersize',3,'markerfacecolor','r')
line([th_m,th_m],[phi_m,phi_m],[0,z_m],'lineStyle','--')
disp([th_m*180/pi,phi_m*180/pi,R_m])
hold off
xlabel('\theta')
ylabel('\phi')
zlabel('R')
title('Alcance')
view(30,25)

 42.1230  146.5497   11.9668

Los ángulos de tiro par los cuales el alcance es máximo R_m=11.97 m, son θ=42.1° y φ=146.5°

Representamos la trayectoria para esta alcance

• Velocidad angular de rotación, ω=1 rad/s
• Distancia al eje de rotación, d=1 m
• Velocidad inicial, v₀=10 m/s
• Angulos de tiro: con la vertical Z, θ= 0.7352, con el eje X, φ=2.5578.

Referencias

J. A. Weyland, J. D. Patterson. Rotating water sprinkler. Am. J. Phys. 44 (11) November 1976, pp. 1106-1109