Ejemplo 1

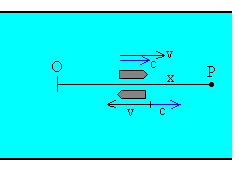
Un río fluye hacia el este con velocidad de c=3 m/s. Un bote se dirige hacia el este (aguas abajo) con velocidad relativa al agua de v=4 m/s.

• Calcular la velocidad del bote respecto de tierra cuando el bote se dirige hacia el este (río abajo) y cuando se dirige hacia el oeste (río arriba).

• Calcular el tiempo que tarda el bote en desplazarse d=100 m hasta el punto P y regresar de nuevo al punto de partida O.



Solución

• Cuando el bote navega aguas abajo la velocidad del bote respecto de tierra es c+v, es decir de 7 m/s.

• Cuando el bote navega en sentido contrario a la corriente la velocidad del bote respecto de tierra es c-v, es decir de -1 m/s.

• El tiempo que tarda el barquero en hacer el viaje de ida es t₁=d/(v+c)

• El tiempo que tarda en hacer el viaje de vuelta es t₂=d/(v-c)

El tiempo total es

${\displaystyle t=t_1+t_2=\frac{2vd}{v^2-c^2}}$

Con los datos del problema t=800/7=114.3 s.

Ejemplo 2

En esta sección el barco atraviesa el río. Pueden ocurrir dos casos:

• Que la velocidad del barco v respecto de la corriente sea mayor que la de la corriente c

• Que la velocidad del barco v respecto de la corriente sea menor que la de la corriente c

Primer caso: v>c

Un río fluye hacia el este con velocidad de c=3 m/s. El bote se mueve en agua quieta con una velocidad de v=4 m/s.

• ¿Cómo debe ser dirigido el bote para que llegue a un punto P situado en la orilla opuesta enfrente de O?

• Calcular la velocidad V del bote respecto de tierra.
• Calcular el tiempo que tarda el bote en desplazarse d=100 m hasta el punto P y regresar de nuevo al punto de partida O.

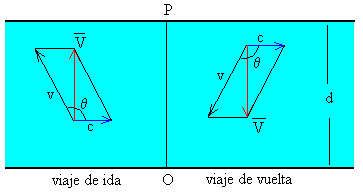
El vector velocidad $\overrightarrow{V}$ del barco respecto de tierra debe de apuntar hacia el norte.

El resultado de la suma $\overrightarrow{V}=\overrightarrow{v}+\overrightarrow{c}$ es

${\displaystyle V\widehat{j}=\left(v\cos \theta ·\widehat{i}+v\sin \theta ·\widehat{j}\right)+c\widehat{i}}$

o bien,

0=c+v·cosθ
V=v·sinθ

• El ángulo θ se calcula a partir de la primera ecuación cosθ=-c/v.

• La velocidad del barco respecto de tierra V se calcula a partir de la segunda ecuación, o bien, como el cateto V del triángulo rectángulo formado por la hipotenusa v y el otro cateto c.

  ${\displaystyle V=\sqrt{v^2-c^2}}$

• El viaje de vuelta es similar al viaje de ida. El tiempo total de viaje será

  ${\displaystyle t=\frac{2d}{\sqrt{v^2-c^2}}}$

Con los datos del problema,

• La velocidad del bote respecto de tierra es de $\sqrt{7}\text{m/s}$

• El ángulo que forma la proa del bote con la dirección este-oeste es θ=138.6º.

• El tiempo total de viaje será t=2·37.6=75.6 s

Segundo caso: v<c

Cuando la velocidad del barco v (respecto de la corriente) es menor que la velocidad de la corriente c, no es posible que el barco atraviese el río sin desviarse.

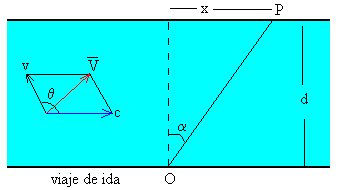
La velocidad del barco respecto de tierra es $\overrightarrow{V}=\overrightarrow{v}+\overrightarrow{c}$

${\displaystyle \overrightarrow{V}=\left(v\cos \theta ·\widehat{i}+v\sin \theta \widehat{j}\right)+c\widehat{i}=\left(v\cos \theta +c\right)\widehat{i}+v\sin \theta \widehat{j}}$

El tiempo t que tarda en cruzar el río de anchura d y la desviación x a lo largo de la orilla es

${\displaystyle t=\frac{d}{v·\sin \theta }x=(c+v\cos \theta )t=(c+v\cos \theta )\frac{d}{v·\sin \theta }}$

La desviación mínima x se produce para el ángulo

${\displaystyle \frac{dx}{d\theta }=\frac{-v^2-vc\cos \theta }{v^2{\cos }^2\theta }=0\cos {\theta }_m=\frac{-v}{c}}$

Introducimos θ_m, en la expresión de la desviación x para calcular la desviación mímina x_m

${\displaystyle x_m=\left(c+\frac{-v}{c}\right)\frac{d}{v\sqrt{1-\frac{v^2}{c^2}}}=d\sqrt{\frac{c^2}{v^2}-1}}$

El tiempo t que tarda en el viaje de ida para el ángulo de desviación mínima θ_m es

${\displaystyle t=\frac{-d}{c·\cos {\theta }_m\sin {\theta }_m}=\frac{-2d}{c·\sin (2{\theta }_m)}}$

El tiempo es mínimo, para el ángulo 2θ_m=270, θ_m=135º

El tiempo de viaje de ida es mínimo, para aquellos botes que se muevan con velocidad v=-c·cos135 haciendo un ángulo θ_m=135º con la dirección de la corriente. El tiempo de viaje y la desviación x es

${\displaystyle t_m=\frac{2d}{c}x=(c-c\cos 135·\cos 135)\frac{d}{-c·\cos 135·\sin 135}=d}$

Ejemplo

Un río fluye hacia el este con velocidad de c=4 m/s. El bote se mueve en agua quieta con una velocidad de v=3 m/s.

El ángulo que hace que la desviación x sea mínima es θ_m=138.6º, la desviación mínima es x_m=88.2 m, el tiempo de viaje es t=50.4 s

Si la velocidad del bote es v=-c·cos135, $v=4\sqrt{3}/2\approx 2.83\text{m/s}$ , el ángulo que produce la desviación mínima es θ_m=135º, la desviación mínima es x_m=100 m, el tiempo de viaje de ida es t_m=50.0 s

Ejemplo 3

Un río fluye hacia el este con velocidad de c=3 m/s. Un bote se dirige hacia el norte θ=90º con velocidad relativa al agua de v=4 m/s.

• Calcular la velocidad del bote respecto de tierra
• Si el río tiene una anchura de d=100 m, calcular el tiempo necesario para cruzarlo.
• ¿Cuál es la desviación hacia el este del bote cuando llega a la otra orilla del río?
• ¿Cómo debe dirigirse el barco para que una vez en el punto P en la orilla opuesta regrese al punto O de partida?
• Calcular el tiempo que tarda en volver al punto de partida

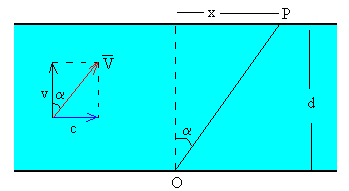
La velocidad del bote respecto de tierra $\overrightarrow{V}$ es la suma vectorial de la velocidad del bote respecto del agua $\overrightarrow{v}$ (cuando el agua está quieta) y la velocidad de la corriente de agua respecto de tierra $\overrightarrow{c}$ .

El resultado de la suma $\overrightarrow{V}=\overrightarrow{v}+\overrightarrow{c}$ es

${\displaystyle V\sin \alpha ·\widehat{i}+V\cos \alpha ·\widehat{j}=c\widehat{i}+v\widehat{j}}$

El módulo del vector resultante $\overrightarrow{V}$ es

${\displaystyle V=\sqrt{c^2+v^2}}$

y forma un ángulo α con la dirección norte-sur

${\displaystyle \tan \alpha =\frac{c}{v}}$

• El tiempo que tarda en el viaje de ida es t₁=d/v,

• La desviación hacia el este es x=c·t₁=c·d/v. O bien, en el triángulo rectángulo de la figura tenemos que x=d·tanα=d·c/v.

Con los datos del problema

• La velocidad del barco respecto de tierra es V=5 m/s y su orientación respecto de la dirección norte-sur es α=36.9º.

• El tiempo que tarda en cruzar el río es t=25 s.

• El desplazamiento hacia el este del barco al llegar a la otra orilla es x=75 m.

La siguiente pregunta ya no es tan fácil. ¿Con qué ángulo debe orientarse la proa del barco para que una vez en el punto P en la orilla opuesta regrese el punto O de partida?.

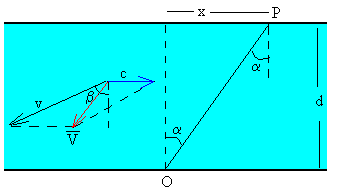
Como puede verse en la figura tenemos que calcular el ángulo β de la dirección de la velocidad $\overrightarrow{v}$ del barco respecto de la corriente para que la velocidad del barco respecto de tierra $\overrightarrow{V}$ forme un ángulo α (calculado anteriormente) con la dirección norte-sur.

El resultado de la suma $\overrightarrow{V}=\overrightarrow{v}+\overrightarrow{c}$ es

${\displaystyle -V\sin \alpha ·\widehat{i}-V\cos \alpha ·\widehat{j}=-v\sin \beta ·\widehat{i}-v\cos \beta \widehat{j}+c·\widehat{i}}$

o bien,

V·sinα=v·sinβ-c
V·cosα= v·cosβ

con tanα=c/v

No resulta difícil demostrar que β=2α. Para ello, se elimina v y V del sistema de ecuaciones.

El tiempo que tarda el barco en regresar al punto de partida O es

${\displaystyle t_2=\frac{d}{v\cos \beta }=\frac{d}{v\cos 2\alpha }=\frac{d}{v}·\frac{(1+{\tan }^2\alpha )}{(1-{\tan }^2\alpha )}=\frac{d}{v}·\frac{(v^2+c^2)}{(v^2-c^2)}}$

Para demostrarlo, se ha empleado la relación trigonométrica 1+tan²α=1/cos²α

El tiempo total de viaje

${\displaystyle t=t_1+t_2=\frac{2dv}{v^2-c^2}}$

Con los datos del problema tenemos

• El ángulo que forma la proa del barco con la dirección este-oeste es θ=90+β=90+2α=163.8º

• El tiempo de viaje de de vuelta t₂=89.3 s y el total t=25+89.3=114.3 s

Comparación de los tiempos de viaje

El tiempo del viaje de ida (t₁=25 s) en el tercer ejemplo es el mínimo para cruzar el río, es menor que en el segundo ejemplo (primer caso v>c) (t₁=37.6 s). Pero el viaje de vuelta en el tercer ejemplo (t₂=89.3 s) es de mayor duración que en el segundo ejemplo (t₂=37.6 s). Por lo que el tiempo de viaje de ida y vuelta en el segundo ejemplo (t=75.6 s) es menor que en el tercer ejemplo (t=114.3 s)  y es el mínimo que se emplea en cruzar el río.

El tiempo de viaje del primer ejemplo (t=114.3 s) es igual al tiempo de viaje en el tercer ejemplo.

Actividades

Se introduce

• La velocidad del barco en agua quieta v, en el control titulado V. barco
• La velocidad de la corriente c, en el control titulado V. corriente
• La dirección de la proa del barco o el ángulo θ que hace con la dirección este-oeste, en el control titulado Angulo.

Se pulsa el botón titulado Nuevo y a continuación, el botón titulado ►.

Cuando el barco llega a la orilla opuesta, se introduce el valor del ángulo θ y se pulsa el botón titulado ►.

Para situar el barco en el origen, se pulsa el botón titulado Nuevo.

El barco se detiene cuando se aleja del origen en la dirección de la corriente más de 100 m. Para situarlo en la posición de partida, basta actuar sobre la barra de desplazamiento que cambia el ángulo θ.

Se introduce

• Velocidad del barco en agua quieta v=4 m/s
• Velocidad de la corriente c=3 m/s

Se pulsa el botón titulado Nuevo

Ejemplo 1

1. Se introduce el ángulo θ=0º
• Se pulsa el botón titulado ►
• Se mide el tiempo t₁ que el barco tarda en recorrer 100 m río abajo

Cuando el barco se detiene

2. Se introduce el ángulo θ=180º
• Se pulsa el botón titulado ►.
• Se mide el tiempo t₂ que el barco tarda en recorrer 100 m río arriba

Se suma los dos tiempos t= t₁+ t₂

Ejemplo 2

Se pulsa el botón titulado Nuevo para situar el barco en el origen

1. Se introduce el dato relativo al ángulo θ=138.6º
• Se pulsa el botón titulado ►
• Se mide el tiempo t₁ que el barco tarda en recorrer 100 m hacia el norte hasta que llegue a la orilla opuesta.

Cuando el barco se detiene

2. Se introduce el dato relativo al ángulo θ=138.6º
• Se pulsa el botón titulado ►.
• Se mide el tiempo t₂ que el barco tarda en recorrer 100 m hacia el sur hasta que regrese al origen

Se suma los dos tiempos t= t₁+ t₂

Ejemplo 3

Se pulsa el botón titulado Nuevo para situar el barco en el origen

1. Se introduce el ángulo θ=90º
• Se pulsa el botón titulado ►
• Se mide el tiempo t₁ que el barco tarda en recorrer 100 m hasta que llegue a la orilla opuesta.

Cuando el barco se detiene

2. Se introduce el dato relativo al ángulo θ=163.8º
• Se pulsa el botón titulado ►.
• Se mide el tiempo t₂ que el barco tarda en recorrer 100 m hacia que regrese al origen.

Se suma los dos tiempos t= t₁+ t₂