Comenzamos esta página con un pequeño juego

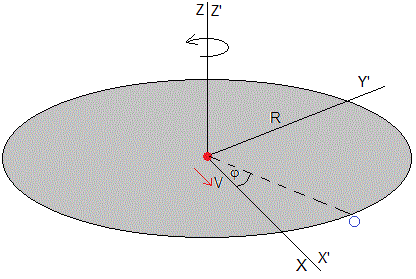
Sea una plataforma circular horizontal, de radio R, que gira con velocidad angular constante ω, alrededor de un eje perpendicular a la plataforma y que pasa por su centro. Cerca de la plataforma hay una canasta O

Un jugador, situado en el centro, lanza una pelota con velocidad v, que desliza sobre la plataforma sin rozamiento en la dirección radial y deberá acertar a introducirla en la canasta.

En la figura se muestra la situación inicial, t=0, la canasta forma un ángulo φ, con la dirección inicial de la velocidad. Veremos que hay infinitas velocidades para encestar

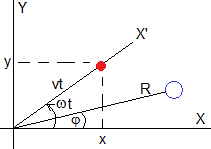
En el instante t, la pelota se encuentra a una distancia vt del origen formando un ángulo ωt con el eje X. Las coordenadas de la partícula son

${\displaystyle \{\begin{array}{l}x=vt·\cos \left(\omega t\right)\\ y=vt·\sin \left(\omega t\right)\end{array}}$

Se encesta en el instante t=R/v, tal que

${\displaystyle \begin{array}{l}\tan \phi =\frac{y}{x}=\tan \left(\omega \frac{R}{v}\right)\\ \phi +2k\pi =\omega \frac{R}{v},k=\mathrm{0,1,2,3...}\end{array}}$

Ejemplo: velocidad angular de rotación de la plataforma, ω=1 rad/s, radio de la plataforma R=1 m. Sea φ=π/6.

${\displaystyle v=\frac{\omega R}{\phi +2k\pi },k=\mathrm{0,1,2,3...}}$

Las velocidades v de la pelota que encestan en la canasta son: 1.91, 0.147, 0.076, ... m/s

Actividades

Se introduce

• La posición angular φ de la canasta en grados
• La velocidad con la que se lanza la pelota desde el centro del disco en rotación
• El radio del disco se ha fijado en R=1 m
• La velocidad angular de rotación se ha fijado en ω=1 rad/s

Se pulsa el botón titulado Nuevo

Movimiento rectilíneo y uniforme

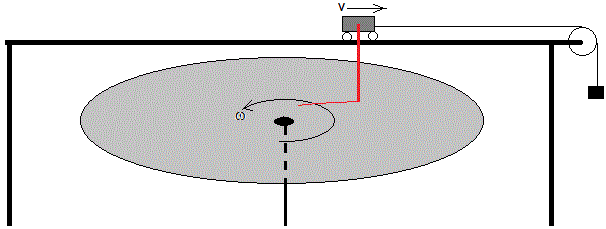
El dispositivo experimental consiste en un carrito que se mueve por una vía rectilínea con velocidad constante v, sobre una plataforma en rotación que gira con velocidad angular constante ω. El carrito dispone de un rotulador, o de un pequeño depósito de tinta, de modo que dibuja su trayectoria rectilínea en el Sistema de Referencia del laboratorio, sobre la plataforma en rotación.

Vector posición

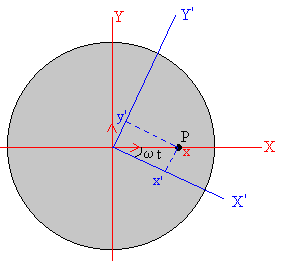
Una partícula P se mueve a lo largo del eje X con velocidad constante v, sabiendo que en el instante inicial t=0, se encuentra en la posición x₀, determinar la trayectoria en el sistema no inercial que gira con velocidad angular constante ω en el sentido de las agujas del reloj.

Sistema inercial

La posición de la partícula P en función del tiempo es

x=x₀+vt
y=0.

El vector posición es $\overrightarrow{r}=x\widehat{i}$

La trayectoria de la partícula es rectilínea

Sistema no inercial

x’=x·cos(ω·t)
y’=x·sin(ω·t)

El vector posición es

${\displaystyle \overrightarrow{r}=x\cos (\omega t)\widehat{i}\text{'}+x\sin (\omega t)\widehat{j}\text{'}}$

Si la partícula parte del origen en el instante t=0, x=v·t. La distancia r de la partícula al origen en el instante t es

${\displaystyle r=\sqrt{v^2{t}^2{\cos }^2(\omega t)+v^2{t}^2{\sin }^2(\omega t)}=vt}$

El ángulo girado por el sistema no inercial al cabo de un cierto tiempo t es θ=ω·t

x0=0;
v=0.1; %velocidad de la partícula
w=2; %velocidad angular de rotación

x=@(t) (x0+v*t).*cos(w*t);
y=@(t) (x0+v*t).*sin(w*t);
fplot(x,y,[0,10])
grid on
axis equal
xlabel('x')
ylabel('y')
title('Movimiento relativo de rotación uniforme')

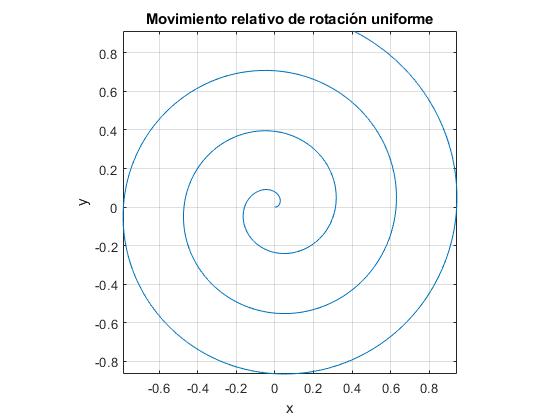
La ecuación de la trayectoria en coordenadas polares es una espiral de Arquímedes

${\displaystyle r=\frac{v}{\omega }\theta }$

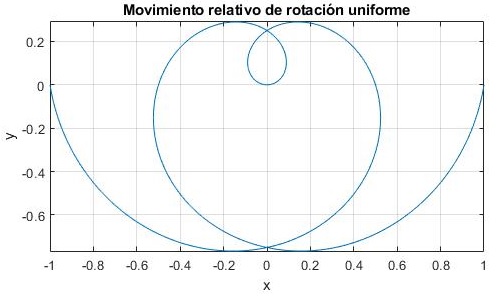
La partícula sale de la posición x₀=-1, se mueve con velocidad v=1/π. Cuando la velocidad angular ω=2, la trayectoria es

x0=-1; %posición inicial
v=1/pi; %velocidad de la partícula
w=2; %velocidad angular de rotación, probar 1,3,4

x=@(t) (x0+v*t).*cos(w*t);
y=@(t) (x0+v*t).*sin(w*t);
fplot(x,y,[0,2*pi])
grid on
axis equal
xlabel('x')
ylabel('y')
title('Movimiento relativo de rotación uniforme')

Vector velocidad

Sistema inercial

La velocidad v de la partícula P es constante $\overrightarrow{v}=v\widehat{i}$

Sistema no inercial

Derivando respecto del tiempo obtenemos la velocidad de la partícula medida en el sistema no inercial

${\displaystyle \begin{array}{l}{v}_x^{\text{'}}=\frac{dx\text{'}}{dt}=v\cos (\omega t)-x\omega \sin (\omega t)\\ v_y^{\text{'}}=\frac{dy\text{'}}{dt}=v\sin (\omega t)+x\omega \cos (\omega t)\end{array}}$

Vamos a comparar este resultado con el que nos proporciona la fórmula (se justifica al final de la página)

${\displaystyle \overrightarrow{v}\text{'}=\overrightarrow{v}-\overrightarrow{\omega }\times \overrightarrow{r}}$

Con

${\displaystyle \begin{array}{l}\overrightarrow{v}=v\widehat{i}\\ \overrightarrow{\omega }=-\omega \widehat{k}\\ \overrightarrow{r}=x\widehat{i}\end{array}}$

se obtiene

${\displaystyle \overrightarrow{v}\text{'}=v\widehat{i}+\omega x\widehat{j}}$

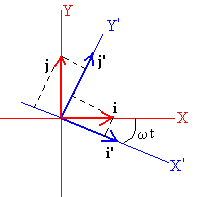
Ahora, relacionamos los vectores unitarios $\widehat{i},\widehat{j}$ , del sistema de referencia OXY inercial con los vectores unitarios $\widehat{i}\text{'},\widehat{j}\text{'}$ del sistema OX’Y’ no inercial

${\displaystyle \begin{array}{l}\widehat{i}=\cos (\omega t)\widehat{i}\text{'}+\sin (\omega t)\widehat{j}\text{'}\\ \widehat{j}=-\sin (\omega t)\widehat{i}\text{'}+\cos (\omega t)\widehat{j}\text{'}\end{array}}$

Obtenemos de nuevo, el vector velocidad $\overrightarrow{v}\text{'}$

${\displaystyle \overrightarrow{v}\text{'}=(v\cos (\omega t)-x\omega \sin (\omega t))\widehat{i}\text{'}+(v\sin (\omega t)+x\omega \cos (\omega t))\widehat{j}\text{'}}$

Vector aceleración

Sistema inercial

La velocidad v de la partícula P es constante en módulo y dirección

${\displaystyle \overrightarrow{a}=0}$

Sistema no inercial

Derivando las componentes de la velocidad con respecto del tiempo obtenemos la aceleración $\overrightarrow{a}\text{'}$ medida en el sistema no inercial.

${\displaystyle \begin{array}{l}{a}_x^{\text{'}}=\frac{d{v}_x^{\text{'}}}{dt}=-2v\omega \sin (\omega t)-x{\omega }^2\cos (\omega t)\\ a_y^{\text{'}}=\frac{d{v}_y^{\text{'}}}{dt}=2v\omega \cos (\omega t)-x{\omega }^2\sin (\omega t)\end{array}}$

Veamos ahora mediante la fórmula (se justifica al final de la página)

${\displaystyle \overrightarrow{a}\text{'}=\overrightarrow{a}-2\overrightarrow{\omega }\times \overrightarrow{v}\text{'}-\overrightarrow{\omega }\times (\overrightarrow{\omega }\times \overrightarrow{r})}$

Los datos que tenemos son

$\overrightarrow{a}=0$ , el movimiento es uniforme en el sistema de referencia inercial

${\displaystyle \begin{array}{l}\overrightarrow{\omega }=-\omega \widehat{k}\\ \overrightarrow{r}=x\cos (\omega t)\widehat{i}\text{'}+x\sin (\omega t)\widehat{j}\text{'}\\ \overrightarrow{v}\text{'}=\left(v\cos (\omega t)-x\omega \sin (\omega t)\right)\widehat{i}\text{'}+\left(v\sin (\omega t)+x\omega \cos (\omega t)\right)\widehat{j}\text{'}\end{array}}$

Calculamos cada aceleración separadamente

Aceleración de Coriolis

${\displaystyle \begin{array}{l}-2\overrightarrow{\omega }\times \overrightarrow{v}\text{'}=-2\left(-\omega \widehat{k}\right)\times \left(v_x\widehat{i}\text{'}+v_y\widehat{j}\text{'}\right)=-2\omega v_y\widehat{i}\text{'}+2\omega v_x\widehat{j}\text{'}=\\ -2\omega \left(v\sin (\omega t)+x\omega \cos (\omega t)\right)\widehat{i}\text{'}+2\omega \left(v\cos (\omega t)-x\omega \sin (\omega t)\right)\widehat{j}\text{'}\end{array}}$

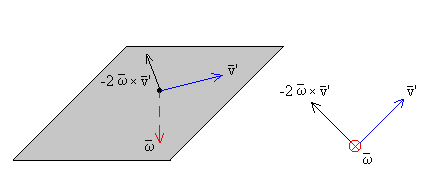
En la figura, se muestra que la aceleración de Coriolis es siempre perpendicular a la velocidad $\overrightarrow{v}\text{'}$ . A la izquierda, se muestra el producto vectorial en el espacio, y a la derecha la misma representación en el plano.

Aceleración centrífuga

${\displaystyle \begin{array}{l}-\overrightarrow{\omega }\times \left(\overrightarrow{\omega }\times \overrightarrow{r}\right)\\ \overrightarrow{r}=x\cos (\omega t)\widehat{i}\text{'}+x\sin (\omega t)\widehat{j}\text{'}\end{array}}$

El resultado del triple producto vectorial es

${\displaystyle =-\left(-\omega \widehat{k}\right)\left(\omega x\sin (\omega t)\widehat{i}\text{'}-\omega x\cos (\omega t)\widehat{j}\text{'}\right)={\omega }^{2}x\cos (\omega t)\widehat{i}\text{'}+{\omega }^{2}x\sin (\omega t)\widehat{j}\text{'}}$

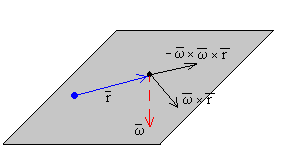
La aceleración centrífuga tiene dirección radial.

Sumando las dos contribuciones volvemos a obtener la aceleración $\overrightarrow{a}\text{'}$ medida en el sistema no inercial

${\displaystyle \overrightarrow{a}\text{'}=\left(-2\omega v\sin (\omega t)-{\omega }^{2}x\cos (\omega t)\right)\widehat{i}\text{'}+\left(2\omega v\cos (\omega t)-{\omega }^{2}x\sin (\omega t)\right)\widehat{j}\text{'}}$

Actividades

Se introduce los siguientes datos:

• La velocidad angular de rotación ω, en el control titulado Velocidad angular
• la velocidad constante de la partícula v, en el control titulado Velocidad del móvil
• la posición inicial de la partícula x₀, en el control titulado Posición inicial

Se pulsa el botón titulado Nuevo

Para ver la representación del vector velocidad, aceleración centrífuga y de Coriolis activar la casilla titulada Vectores.

Ejemplos

• Posición inicial, x₀=0
• Velocidad del móvil, v=0.1
• Velocidad angular de rotación, ω=2

Otro ejemplo

• Posición inicial, x₀=0.9
• Velocidad del móvil, v=x₀/π=0.2865
• Velocidad angular de rotación, ω=2

Se detiene el movimiento cuando el móvil llegue a la posición diametralmente opuesta, x=0.9. Cambiar la velocidad angular a 1, 3, 4

Oscilaciones

Supongamos que una partícula describe un Movimiento Armónico Simple de frecuencia angular ω_p en el Sistema de Referencia Inercial.

x=Acos(ω_pt)

Se dibuja la trayectoria en el sistema no inercial OX’Y’ aplicando la transformación

x’=x·cos(ω t)=Acos(ω_pt)·cos(ω t)
y’=x·sin(ω t)=Acos(ω_pt)·sin(ω t)

Donde ω es la velocidad angular de rotación

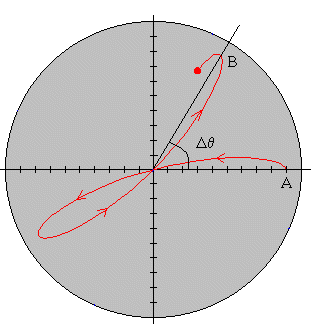
En la figura, se muestra el ángulo girado por el plano de oscilación del "péndulo" durante el periodo de una oscilación. El péndulo parte de A y regresa a B, para iniciar una nueva oscilación. El ángulo girado es Δθ =ω·P. Siendo P=2π/ω_p el periodo de una oscilación

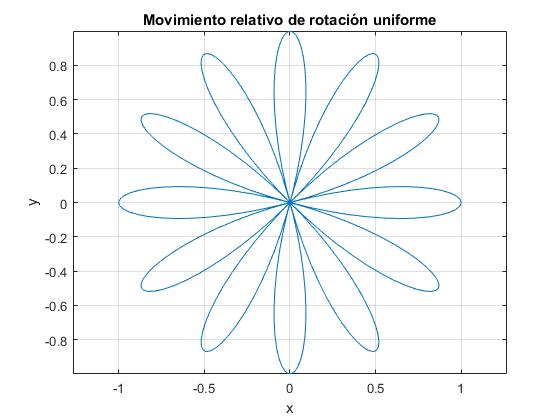
wp=6;
w=1;

t=0:0.02:2*pi;
x=cos(wp*t).*cos(w*t);
y=cos(wp*t).*sin(w*t);
plot(x,y)
grid on
axis equal
xlabel('x')
ylabel('y')
title('Movimiento relativo de rotación uniforme')

Caso particular ω =ω_p

Las ecuaciones paramétricas de la trayectoria son

${\displaystyle \begin{array}{l}x\text{'}=A\cos (\omega t)\cos (\omega t)=\frac{A}{2}\left(1+\cos (2\omega t)\right)\\ y\text{'}=A\cos (\omega t)\sin (\omega t)=\frac{A}{2}\sin (2\omega t)\end{array}}$

Eliminamos el tiempo t de las ecuaciones paramétricas de la trayectoria y obtenemos la ecuación de una circunferencia centrada en el punto (A/2, 0) y de radio A/2.

Actividades

Se introduce

• La velocidad angular ω de rotación, un número entero, en el control titulado Velocidad angular
• La frecuencia angular ω_p del MAS, un número entero, en el control titulado Frecuencia angular

Se pulsa el botón titulado Nuevo

Movimiento relativo de rotación uniforme

Comenzamos con la derivada con respecto del tiempo, de un vector de módulo constante

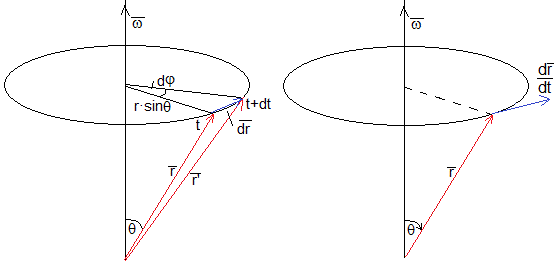
• En el instante t, el vector posción es $\overrightarrow{r}$

• En el instante t+dt, el vector posción es $\overrightarrow{r\text{'}}$

• El vector diferencia es el vector $d\overrightarrow{r}$ , que es tangente a la circunferencia de radio r·sinθ. Su módulo es

${\displaystyle \begin{array}{l}dr=r\sin \theta ·d\phi \\ \frac{dr}{dt}=r\sin \theta \frac{d\phi }{dt}=r\sin \theta ·\omega \end{array}}$

donde ω es la velocidad angular de rotación constante. En forma vectorial escribimos

${\displaystyle \frac{d\overrightarrow{r}}{dt}=\overrightarrow{\omega }\times \overrightarrow{r}}$

Sistema de Referencia inercial, O XYZ

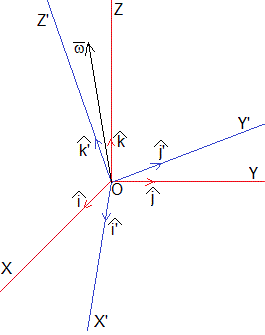
Vector posición, velocidad y aceleración

${\displaystyle \begin{array}{l}\overrightarrow{r}=x\widehat{i}+y\widehat{j}+z\widehat{k}\\ \overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\frac{dx}{dt}\widehat{i}+\frac{dy}{dt}\widehat{j}+\frac{dz}{dt}\widehat{k},\{\begin{array}{l}{v}_x=\frac{dx}{dt}\\ v_y=\frac{dy}{dt}\\ v_z=\frac{dz}{dt}\end{array}\\ \overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{d^2\overrightarrow{r}}{d{t}^2}=\frac{d{v}_x}{dt}\widehat{i}+\frac{d{v}_y}{dt}\widehat{j}+\frac{d{v}_z}{dt}\widehat{k}\end{array}}$

Sistema de Referencia no inercial O X'Y'Z'

• Vector posición

${\displaystyle \overrightarrow{r}=x\widehat{\text{'}i\text{'}}+y\text{'}\widehat{j\text{'}}+z\text{'}\widehat{k\text{'}}}$

• Vector velocidad

${\displaystyle \begin{array}{l}\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\frac{dx\text{'}}{dt}\widehat{i\text{'}}+\frac{dy\text{'}}{dt}\widehat{j\text{'}}+\frac{dz\text{'}}{dt}\widehat{k\text{'}}+x\text{'}\frac{d\widehat{i\text{'}}}{dt}+y\text{'}\frac{d\widehat{j\text{'}}}{dt}+z\text{'}\frac{d\widehat{k\text{'}}}{dt}=\\ \frac{dx\text{'}}{dt}\widehat{i\text{'}}+\frac{dy\text{'}}{dt}\widehat{j\text{'}}+\frac{dz\text{'}}{dt}\widehat{k\text{'}}+x\text{'}\overrightarrow{\omega }\times \widehat{i\text{'}}+y\text{'}\overrightarrow{\omega }\times \widehat{j\text{'}}+z\text{'}\overrightarrow{\omega }\times \widehat{k\text{'}}=\\ \frac{dx\text{'}}{dt}\widehat{i\text{'}}+\frac{dy\text{'}}{dt}\widehat{j\text{'}}+\frac{dz\text{'}}{dt}\widehat{k\text{'}}+\overrightarrow{\omega }\times \left(x\text{'}\widehat{i\text{'}}+y\text{'}\widehat{j\text{'}}+z\text{'}\widehat{k\text{'}}\right)\\ \overrightarrow{v}=\overrightarrow{v\text{'}}+\overrightarrow{\omega }\times \overrightarrow{r}\end{array}}$

• Vector aceleración

${\displaystyle \overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{d\overrightarrow{v\text{'}}}{dt}+\overrightarrow{\omega }\times \frac{d\overrightarrow{r}}{dt}+\frac{d\overrightarrow{\omega }}{dt}\times \overrightarrow{r}}$

El primer término es

${\displaystyle \begin{array}{l}\frac{d\overrightarrow{v\text{'}}}{dt}=\frac{d{v}_x^{\text{'}}}{dt}\widehat{i\text{'}}+\frac{d{v}_y^{\text{'}}}{dt}\widehat{j\text{'}}+\frac{d{v}_z^{\text{'}}}{dt}\widehat{k\text{'}}+v_x^{\text{'}}\frac{d\widehat{i\text{'}}}{dt}+v_y^{\text{'}}\frac{d\widehat{j\text{'}}}{dt}+v_z^{\text{'}}\frac{d\widehat{k\text{'}}}{dt}=\\ \frac{d{v}_x^{\text{'}}}{dt}\widehat{i\text{'}}+\frac{d{v}_y^{\text{'}}}{dt}\widehat{j\text{'}}+\frac{d{v}_z^{\text{'}}}{dt}\widehat{k\text{'}}+v_x^{\text{'}}\overrightarrow{\omega }\times \widehat{i\text{'}}+v_y^{\text{'}}\overrightarrow{\omega }\times \widehat{j\text{'}}+v_z^{\text{'}}\overrightarrow{\omega }\times \widehat{k\text{'}}=\\ \frac{d{v}_x^{\text{'}}}{dt}\widehat{i\text{'}}+\frac{d{v}_y^{\text{'}}}{dt}\widehat{j\text{'}}+\frac{d{v}_z^{\text{'}}}{dt}\widehat{k\text{'}}+\overrightarrow{\omega }\times \left(v_x^{\text{'}}\widehat{i\text{'}}+v_y^{\text{'}}\widehat{j\text{'}}+v_z^{\text{'}}\widehat{k\text{'}}\right)=\\ \overrightarrow{a\text{'}}+\overrightarrow{\omega }\times \overrightarrow{v\text{'}}\end{array}}$

El segundo término es

${\displaystyle \overrightarrow{\omega }\times \frac{d\overrightarrow{r}}{dt}=\overrightarrow{\omega }\times \left(\overrightarrow{v\text{'}}+\overrightarrow{\omega }\times \overrightarrow{r}\right)=\overrightarrow{\omega }\times \overrightarrow{v\text{'}}+\overrightarrow{\omega }\times \left(\overrightarrow{\omega }\times \overrightarrow{r}\right)}$

La suma de los tres términos es

${\displaystyle \overrightarrow{a}=\overrightarrow{a\text{'}}+2\left(\overrightarrow{\omega }\times \overrightarrow{v\text{'}}\right)+\overrightarrow{\omega }\times \left(\overrightarrow{\omega }\times \overrightarrow{r}\right)+\frac{d\overrightarrow{\omega }}{dt}\times \overrightarrow{r}}$

Habitualmente, la velocidad angular $\overrightarrow{\omega }$ es constante

${\displaystyle \overrightarrow{a}=\overrightarrow{a\text{'}}+2\left(\overrightarrow{\omega }\times \overrightarrow{v\text{'}}\right)+\overrightarrow{\omega }\times \left(\overrightarrow{\omega }\times \overrightarrow{r}\right)}$

Referencias

Lenka Czudková, Jana Musilová. Physics in a lift and on turntable. Phys. Educ. 35 (1) January 2000, pp. 22-29

Marcelo Alonso, Edward J. Finn. Física, Mecánica. Fondo Educativo Interamericano. 1976, pp. 126-128