Movimiento rectilíneo horizontal

El caso más sencillo se produce cuando la trayectoria del submarino es una recta horizontal y=h

El torpedo A se mueve con velocidad constante v (en módulo) apuntando a la submarino B que se mueve a lo largo de la línea recta de pendiente α con velocidad constante u. El torpedo A sale del origen en el instante t=0, y la submarino sale del punto (0,h) en el mismo instante.

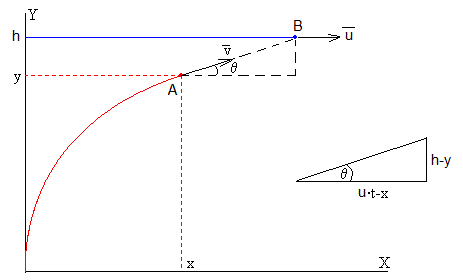
En el triángulo rectángulo de la figura, la base es la diferencia entre el desplazamiento del submarino u·t y la del torpedo x. La altura es la diferencia h-y. Como la dirección de la velocidad del torpedo es la línea recta que pasa por la posición del torpedo y la del submarino en el instante t, tendremos que

${\displaystyle \tan \theta =\frac{v_y}{v_x}=\frac{h-y}{u·t-x}v=\sqrt{v_x^2+v_y^2}}$

o de forma alternativa

${\displaystyle u·t-x=(h-y)\frac{v_x}{v_y}}$

Diferenciando ambos miembros con respecto del tiempo

${\displaystyle \begin{array}{l}u-v_x=-v_y\frac{v_x}{v_y}+(h-y)\frac{d}{dt}\left(\frac{v_x}{v_y}\right)\frac{u}{h-y}=\frac{d}{dt}\sqrt{\frac{v^2}{v_y^2}-1}\\ \frac{u}{h-y}=\frac{-v^2}{v_y^2\sqrt{v^2-v_y^2}}\frac{d{v}_y}{dt}\end{array}}$

Teniendo en cuenta que

${\displaystyle \begin{array}{l}\frac{d{v}_y}{dt}=\frac{dy}{dt}\frac{d{v}_y}{dy}=v_y\frac{d{v}_y}{dy}\\ \frac{u}{h-y}dy=\frac{-v^2}{v_y\sqrt{v^2-v_y^2}}d{v}_y\end{array}}$

Integramos ambos miembros, sabiendo que el torpedo parte del origen y=0, y su velocidad inicial es v_y=v, dirigida a lo largo del eje Y.

${\displaystyle {\displaystyle {\int }_0^y\frac{u}{h-y}dy}=-v^2{\displaystyle {\int }_v^{v_y}\frac{d{v}_y}{v_y\sqrt{v^2-v_y^2}}}}$

Para resolver la integral de la derecha, se hace el cambio de variable z=1/v_y

${\displaystyle {\displaystyle \int \frac{-dz}{\sqrt{v^2{z}^2-1}}}=-\frac{1}{v}\ln \left|vz+\sqrt{v^2{z}^2-1}\right|+c}$

Deshaciendo el cambio de variable y evaluando ambas integrales en los límites inferior y superior, se obtiene.

${\displaystyle \begin{array}{l}-\frac{u}{v}\ln \left(\frac{h-y}{h}\right)=\ln \left(\frac{v+\sqrt{v^2-v_y^2}}{v_y}\right)\\ v_y{\left(1-\frac{y}{h}\right)}^{-u/v}-v=\sqrt{v^2-v_y^2}\end{array}}$

Elevando ambos miembros al cuadrado y despejando v_y

${\displaystyle v_y=\frac{2v}{{\left(1-\frac{y}{h}\right)}^{u/v}+{\left(1-\frac{y}{h}\right)}^{-u/v}}}$

Resolvemos la ecuación diferencial de primer orden

${\displaystyle \frac{dy}{dt}-\frac{2v}{{\left(1-\frac{y}{h}\right)}^{u/v}+{\left(1-\frac{y}{h}\right)}^{-u/v}}=0}$

con las condiciones iniciales siguientes: en el instante t=0, el torpedo parte del origen, y=0.

Alternativamente, integramos de nuevo para obtener la ordenada y del torpedo en función del tiempo t.

Para ello, hacemos el cambio de variable z=1-y/h.

${\displaystyle \begin{array}{l}-h{\displaystyle \underset{1}{\overset{z}{\int }}\left(z^{u/v}+z^{-u/v}\right)}dz={\displaystyle \underset{0}{\overset{t}{\int }}2v·dt}\\ t=-\frac{h}{2}\left\{\frac{z^{u/v+1}}{u+v}+\frac{z^{-u/v+1}}{-u+v}-\frac{2v}{-u^2+v^2}\right\}\end{array}}$

Esta es una ecuación implícita de la ordenada y en función del tiempo t.

Una vez obtenida la ordenada y en función del tiempo t, se calcula la abscisa x, mediante la relación deducida al principio de esta página.

${\displaystyle \begin{array}{l}u·t-x=(h-y)\frac{v_x}{v_y}\\ x=u·t-hz\frac{v_x}{v_y}\\ v_y=\frac{2v}{z^{u/v}+z^{-u/v}}{v}_x=\sqrt{v^2-v_y^2}=v\frac{1-z^{2u/v}}{1+z^{2u/v}}\end{array}}$

Sustituimos el tiempo t y obtenemos la ecuación de la trayectoria

${\displaystyle \begin{array}{l}\frac{x}{h}=\frac{1}{2}\frac{z^{1+u/v}}{1+u/v}-\frac{1}{2}\frac{z^{1-u/v}}{1-u/v}+\frac{u/v}{1-u^2/v^2}\\ \frac{x}{h}=\frac{1}{2}\frac{{\left(1-\frac{y}{h}\right)}^{1+n}}{1+n}-\frac{1}{2}\frac{{\left(1-\frac{y}{h}\right)}^{1-n}}{1-n}+\frac{n}{1-n^2},n=\frac{u}{v}\end{array}}$

Distintos casos

• Cuando la velocidad del torpedo es mayor que la del submarino, v>u.

Cuando y=h ó z=0 se produce el impacto del torpedo y la posible destrucción del submarino.

La posición del punto de impacto es

${\displaystyle x=h\frac{u/v}{1-u^2/v^2}}$

que es positivo solamente si v>u. La velocidad v del torpedo tiene que ser necesariamente mayor que la velocidad u del submarino para que haya impacto.

Sea un torpedo y un submarino tal que la relación de velocidades n=u/v=0.5

n=0.5; %relación u/v
x=@(y) 0.5*(1-y).^(1+n)/(1+n)-0.5*(1-y).^(1-n)/(1-n)+n/(1-n^2);
xt=n/(1-n^2); %encuentro
h=1;
hold on
fplot(x,[0,1],'k'); %trayectoria toerpedo
line([h,h],[0,xt],'color','b') %submarino
plot(h,xt,'ro','markersize',4,'markerfacecolor','r') %impacto
line([0,h],[xt,xt],'lineStyle','--')
hold off
view([90 -90])
grid on
xlim([0,1.1])
xlabel('y/h')
ylabel('x/h')
title('Torpedo-submarino')



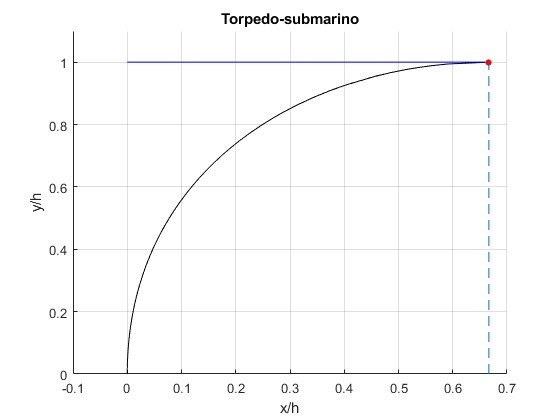
En azul la trayectoria rectilínea del submarino, en negro, la del torpedo. El punto de color rojo señala la posición de encuentro

El instante t en el que se produce es

${\displaystyle t=h\frac{v}{v^2-u^2}}$

• Cuando la velocidad del torpedo es menor que la del submarino, v<u.

El torpedo y el submarino se aproximan hasta una distancia mínima y luego se alejan.

${\displaystyle L=\sqrt{{(u·t-x)}^2+{(h-y)}^2}=(h-y)\frac{v}{v_y}=hz\frac{v}{v_y}=\frac{h}{2}\left(z^{1-u/v}+z^{1-u/v}\right)}$

El mínimo se obtiene derivando L respecto de z e igualando a cero.

${\displaystyle \left(1-\frac{u}{v}\right)z^{-u/v}+\left(1+\frac{u}{v}\right)z^{u/v}=0}$

Haciendo algunas operaciones obtenemos

${\displaystyle L_{\min }=\frac{h}{\sqrt{1-v^2/u^2}}{\left(\frac{u-v}{u+v}\right)}^{v/(2u)}}$

• Cuando la velocidad del submarino y del torpedo es la misma, u=v.

La componente Y de la velocidad del torpedo vale

${\displaystyle \frac{dy}{dt}=\frac{2v}{\left(1-\frac{y}{h}\right)+{\left(1-\frac{y}{h}\right)}^{-1}}}$

Hacemos el cambio de variable z=1-y/H para integrar

${\displaystyle \begin{array}{l}-h{\displaystyle \underset{1}{\overset{z}{\int }}\left(z+\frac{1}{z}\right)}dz={\displaystyle \underset{0}{\overset{t}{\int }}2v·dt}\\ t=\frac{h}{4v}(1-z^2-2\ln z)\end{array}}$

La ecuación de la trayectoria es

${\displaystyle \begin{array}{l}\frac{x}{h}=\frac{z^2-1}{4}-\frac{1}{2}\ln z\\ \frac{x}{h}=\frac{{\left(1-\frac{y}{h}\right)}^2-1}{4}-\frac{1}{2}\ln \left(1-\frac{y}{h}\right)\end{array}}$

Cuando v→u, la distancia entre el submarino L_min y el torpedo tiende a h/2, como puede comprobarse fácilmente

Representamos x/h en función de y/h en el intervalo 0≤y≤h para varios valores del cociente k=u/v. Cuando v>u o n<1 (primer caso) se produce el impacto. v=u o n=1 es el caso límite

hold on
for n=[5,2,1,0.5,0.2]
    x=@(y) 0.5*(1-y).^(1+n)/(1+n)-0.5*(1-y).^(1-n)/(1-n)+n/(1-n^2);
    if n==1
        x=@(y) ((1-y).^2-1)/4-log(sqrt(1-y));
    end
    fplot(x,[0,1], 'displayName',num2str(n));
end
hold off
legend('-DynamicLegend','location','southeast')
view([90 -90])
ylim([0,2])
grid on
ylabel('x/h')
xlabel('y/h')
title('Gráfica de la ecuación')

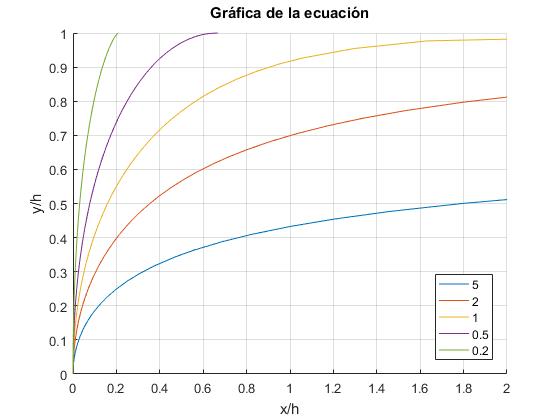
Ejemplo.

• Cuando la velocidad v del torpedo es menor que la del submarino u=1. Por ejemplo, v=0.8.

La distancia de máximo acercamiento es

${\displaystyle L_{\min }=\frac{1.0}{\sqrt{1-{0.8}^2}}{\left(\frac{1-0.8}{1+0.8}\right)}^{0.8/2}=0.692}$

En la posición

${\displaystyle \begin{array}{l}\left(1-\frac{u}{v}\right)z^{-u/v}+\left(1+\frac{u}{v}\right)z^{u/v}=0\\ -0.25·z^{-1.25}+2.25·z^{1.25}=0\end{array}}$

z=0.415, y=0.585

En el instante

${\displaystyle \begin{array}{l}t=-\frac{h}{2}\left\{\frac{z^{u/v+1}}{u+v}+\frac{z^{-u/v+1}}{-u+v}-\frac{2v}{-u^2+v^2}\right\}\\ t=-\frac{1}{2}\left\{\frac{{0.415}^{}}{1.8}+\frac{{0.415}^{-0.25}}{-0.2}-\frac{2·0.8}{-1^2+{0.8}^2}\right\}=0.854\end{array}}$

La abscisa x se obtiene a partir de la ecuación de la trayectoria

${\displaystyle \begin{array}{l}\frac{x}{h}=\frac{1}{2}·\frac{z^{1+u/v}}{1+u/v}-\frac{1}{2}·\frac{z^{1-u/v}}{1-u/v}+\frac{u/v}{1-u^2/v^2}\\ x=\frac{1}{2}\frac{{0.415}^{2.25}}{2.25}-\frac{1}{2}\frac{{0.415}^{-0.25}}{-0.25}+\frac{1.25}{1-{1.25}^2}=0.300\end{array}}$

• Cuando la velocidad v del torpedo es mayor que la del submarino u=1. Por ejemplo, v=2.

La posición del punto de impacto es

${\displaystyle \begin{array}{l}x=h\frac{u/v}{1-u^2/v^2}\\ x=1·\frac{0.5}{1-{0.5}^2}=\frac{2}{3}\end{array}}$

en el instante

${\displaystyle \begin{array}{l}t=h\frac{v}{v^2-u^2}\\ t=1·\frac{2}{2^2-1^2}=\frac{2}{3}\end{array}}$

Actividades

Se introduce

• La velocidad v del torpedo, en el control titulada Velocidad torpedo.

• La velocidad u del submarino se ha fijado en u=1

• La distancia inicial h entre el torpedo y el submarino se ha fijado en h=1.

Se pulsa el botón titulado Nuevo.

Se observa la trayectoria curvilínea del torpedo (en color rojo) y la rectilínea del submarino (en color azul).

La flecha de color negro, representa la velocidad del torpedo, su dirección es tangente a la trayectoria que es a su vez, la recta que une el torpedo y el submarino.

El programa interactivo resuelve numéricamente la ecuación diferencial de primer orden que proporciona el valor de la ordenada y en función del tiempo t, y luego calcula la abscisa x, mediante la relación geométrica establecida al principio de esta página.

Movimiento rectilíneo

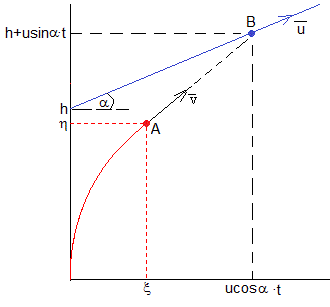
El torpedo A se mueve con velocidad constante v (en módulo) apuntando a la submarino B que se mueve a lo largo de la línea recta de pendiente α con velocidad constante u. El torpedo A sale del origen en el instante t=0, y la submarino sale del punto (0,h) en el mismo instante.

El vector que une los puntos A (ξ, η) y B (ucosα·t, h+usinα·t) tiene la misma dirección que el vector $\overrightarrow{v}$

${\displaystyle \begin{array}{l}\overrightarrow{AB}=\lambda \overrightarrow{v}\\ \{\begin{array}{l}u\cos \alpha ·t-\xi =\lambda v_{\xi },v_{\xi }=\frac{d\xi }{dt}\\ h+u\sin \alpha ·t-\eta =\lambda v_{\eta },v_{\eta }=\frac{d\eta }{dt}\end{array}\\ v^2=v_{\xi }^2+v_{\eta }^2\end{array}}$

El módulo de la velocidad del torpedo v es constante

Sistema de Referencia girado

Para resolver el problema, adoptamos un sistema de ejes de modo que el eje Y tiene la dirección de la velocidad de la submarino $\overrightarrow{u}$ y el eje X es perpendicular

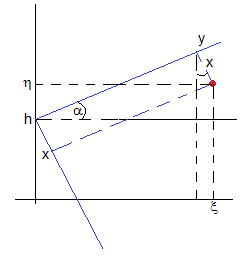
Las coordendas del punto de color rojo son (ξ, η) y en el Sistema de Referencia trasladado a (0, h) y girado un ángulo α son (x, y). La relación entre ambas es

${\displaystyle \{\begin{array}{l}\xi =y\cos \alpha +x\sin \alpha \\ \eta =h+y\sin \alpha -x\cos \alpha \end{array}}$

Las posiciones del torpedo A y de la submarino B coinciden cuando, ξ=ucosα·t y η=h+usinα·t

${\displaystyle \{\begin{array}{l}u\cos \alpha ·t=y\cos \alpha +x\sin \alpha \\ h+u\sin \alpha ·t=h+y\sin \alpha -x\cos \alpha \end{array}}$

Multiplicando la primera por sinα y la segunda por -cosα, despejamos x y lo denominamos x_t. Multiplicando la primera por cosα y la segunda por sinα, despejamos y y lo denominamos y_t

En la posición x_t=0, y_t=ut, coinciden el torpedo A y el submarino B

Ecuación de la trayectoria

Dado ξ y η despejamos x e y

${\displaystyle \begin{array}{l}\{\begin{array}{l}x=h\cos \alpha +\xi \sin \alpha -\eta \cos \alpha \\ y=-h\sin \alpha +\xi \cos \alpha +\eta \sin \alpha \end{array}\\ \{\begin{array}{l}\frac{dx}{dt}=\frac{d\xi }{dt}\sin \alpha -\frac{d\eta }{dt}\cos \alpha \\ \frac{dy}{dt}=\frac{d\xi }{dt}\cos \alpha +\frac{d\eta }{dt}\sin \alpha \end{array}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\{\begin{array}{l}x=h\cos \alpha +\left(u\cos \alpha ·t-\lambda v_{\xi }\right)\sin \alpha -\left(h+u\sin \alpha ·t-\lambda v_{\eta }\right)\cos \alpha \\ y=-h\sin \alpha +\left(u\cos \alpha ·t-\lambda v_{\xi }\right)\cos \alpha +\left(h+u\sin \alpha ·t-\lambda v_{\eta }\right)\sin \alpha \end{array}\\ \{\begin{array}{l}x=-\lambda \left(v_{\xi }\sin \alpha -v_{\eta }\cos \alpha \right)\\ y=ut-\lambda \left(v_{\xi }\cos \alpha +v_{\eta }\sin \alpha \right)\end{array}\\ \{\begin{array}{l}x=-\lambda \frac{dx}{dt}\\ y=ut-\lambda \frac{dy}{dt}\end{array}\end{array}}$

Obtenemos un sistema de dos ecuaciones diferenciales, a la que hay que añadir una tercera, que indica que el módulo de la velocidad del torpedo v es constante

${\displaystyle {\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2=v^2}$

Eliminamos el parámetro λ de las dos primeras ecuaciones

${\displaystyle \begin{array}{l}y=ut+x\frac{\frac{dy}{dt}}{\frac{dx}{dt}}\\ y-x\frac{dy}{dx}=ut\end{array}}$

Derivamos con respecto de x

${\displaystyle -x\frac{d^{2}y}{d{x}^2}=u\frac{dt}{dx}}$

Por otra parte, la tercera ecuación se escribe, dividiendo por el primer término (dx/dt)²

${\displaystyle 1+{\left(\frac{dy}{dx}\right)}^2=v^2{\left(\frac{dt}{dx}\right)}^2}$

Obtenemos la ecuación diferencial

${\displaystyle -x\frac{d^{2}y}{d{x}^2}=\pm \frac{u}{v}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}$

Tomamos la raíz negativa de modo que d²y/dx² sea positiva

${\displaystyle \begin{array}{l}x\frac{d^{2}y}{d{x}^2}=\frac{u}{v}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}\\ x\frac{dp}{dx}=\frac{u}{v}\sqrt{1+p^2},p=\frac{dy}{dx}\end{array}}$

Separamos las variables e integramos

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{dp}{\sqrt{1+p^2}}}=\frac{u}{v}{\displaystyle \int \frac{dx}{x}}\\ \ln \left(p+\sqrt{1+p^2}\right)=\frac{u}{v}\ln x+\frac{u}{v}\ln x_c\end{array}}$

donde el último término es la constante de integración

${\displaystyle \begin{array}{l}\ln \left(p+\sqrt{1+p^2}\right)=\ln {\left(\frac{x}{x_c}\right)}^n,n=\frac{u}{v}\\ p+\sqrt{1+p^2}={\left(\frac{x}{x_c}\right)}^n\end{array}}$

La inversa de esta ecuación es

${\displaystyle -p+\sqrt{1+p^2}={\left(\frac{x}{x_c}\right)}^{-n}}$

Restando ambas ecuaciones obtenemos

${\displaystyle p=\frac{dy}{dx}=\frac{1}{2}\left\{{\left(\frac{x}{x_c}\right)}^n-{\left(\frac{x}{x_c}\right)}^{-n}\right\}}$

Las condiciones iniciales determinan la constante de integración x_c

En el instante t=0, el torpedo A parte de ξ=0, y η=0. En el Sistema de Referencia girado, x₀=hcosα, y₀=-hsinα. De la ecuación

${\displaystyle \begin{array}{l}y-x\frac{dy}{dx}=ut\\ {\left(\frac{dy}{dx}\right)}_{t=0}=\frac{y_0}{x_0}\\ {\left(\frac{dy}{dx}\right)}_{t=0}=-\tan \alpha \end{array}}$

En el instante t=0, x=x₀

${\displaystyle \begin{array}{l}-\tan \alpha =\frac{1}{2}\left\{{\left(\frac{h\cos \alpha }{x_c}\right)}^n-{\left(\frac{h\cos \alpha }{x_c}\right)}^{-n}\right\}\\ z^{2n}+2\tan \alpha ·z^n-1=\mathrm{0,}z=\frac{h\cos \alpha }{x_c}\\ z^n=-\tan \alpha \pm \frac{1}{\cos \alpha }\end{array}}$

Tomamos la raíz positiva

${\displaystyle \begin{array}{l}{z}^n=\frac{1-\sin \alpha }{\cos \alpha }\\ \frac{h\cos \alpha }{x_c}={\left(\frac{1-\sin \alpha }{\cos \alpha }\right)}^{1/n}\\ x_c={\left(\frac{\cos \alpha }{1-\sin \alpha }\right)}^{1/n}h\cos \alpha \end{array}}$

Casos

• Las velocidades del torpedo v y del submarino u son distintas, u≠v

${\displaystyle \begin{array}{l}{\displaystyle \underset{y_0}{\overset{y}{\int }}dy}=\frac{1}{2}{\displaystyle \underset{x_0}{\overset{x}{\int }}\left\{\frac{x^n}{x_c^n}-\frac{x^{-n}}{x_c^{-n}}\right\}dx}\\ y-y_0=\frac{1}{2}\left\{\frac{1}{n+1}\frac{x^{n+1}-x_0^{n+1}}{x_c^n}-\frac{1}{-n+1}\frac{x^{-n+1}-x_0^{-n+1}}{x_c^{-n}}\right\}\\ y+h\sin \alpha =\frac{1}{2}\left\{\frac{1}{n+1}\frac{1-\sin \alpha }{\cos \alpha }\frac{x^{n+1}-{\left(h\cos \alpha \right)}^{n+1}}{{\left(h\cos \alpha \right)}^n}-\frac{1}{-n+1}\frac{\cos \alpha }{1-\sin \alpha }\frac{x^{-n+1}-{\left(h\cos \alpha \right)}^{-n+1}}{{\left(h\cos \alpha \right)}^{-n}}\right\}\\ y+h\sin \alpha =\frac{1}{2}\left\{\frac{1}{n+1}\frac{\left(1-\sin \alpha \right)}{\cos \alpha }\frac{x^{n+1}-{\left(h\cos \alpha \right)}^{n+1}}{{\left(h\cos \alpha \right)}^{n+1}}h\cos \alpha -\frac{1}{-n+1}\frac{\cos \alpha }{\left(1-\sin \alpha \right)}\frac{x^{-n+1}-{\left(h\cos \alpha \right)}^{-n+1}}{{\left(h\cos \alpha \right)}^{-n+1}}h\cos \alpha \right\}\\ y=-h\sin \alpha +\frac{1}{2}\left\{\frac{h}{n+1}\left(1-\sin \alpha \right)\left({\left(\frac{x}{h\cos \alpha }\right)}^{1+n}-1\right)-\frac{1}{1-n}\frac{h{\cos }^2\alpha }{\left(1-\sin \alpha \right)}\left({\left(\frac{x}{h\cos \alpha }\right)}^{1-n}-1\right)\right\}\\ y=-h\sin \alpha +\frac{1}{2}\left\{-\frac{h}{1+n}\left(1-\sin \alpha \right)+\frac{1}{1-n}\frac{h\left(1-{\sin }^2\alpha \right)}{\left(1-\sin \alpha \right)}\right\}+\frac{1}{2}\left\{\frac{h}{1+n}\left(1-\sin \alpha \right){\left(\frac{x}{h\cos \alpha }\right)}^{1+n}-\frac{1}{1-n}\frac{h{\cos }^2\alpha }{\left(1-\sin \alpha \right)}{\left(\frac{x}{h\cos \alpha }\right)}^{1-n}\right\}\end{array}}$

El resultado final es

${\displaystyle y=h\frac{n\left(1+n\sin \alpha \right)}{1-n^2}+\frac{h}{2}\left\{\frac{1-\sin \alpha }{1+n}{\left(\frac{x}{h\cos \alpha }\right)}^{1+n}-\frac{1+\sin \alpha }{1-n}{\left(\frac{x}{h\cos \alpha }\right)}^{1-n}\right\}}$

Es la ecuación de la trayectoria del torpedo en el Sistema de Referencia girado. La trayectoria real es

${\displaystyle \{\begin{array}{l}\xi =y\cos \alpha +x\sin \alpha \\ \eta =h+y\sin \alpha -x\cos \alpha \end{array}}$

El torpedo alcanza al submarino en la posición (Sistema de Referencia girado)

${\displaystyle \{\begin{array}{l}{x}_t=0\\ y_t=h\frac{n\left(1+n\sin \alpha \right)}{1-n^2}\end{array}}$

El tiempo T que tarda en alcazarlo es

${\displaystyle T=\frac{y_t}{u}=\frac{h}{u}\frac{n\left(1+n\sin \alpha \right)}{1-n^2}=h\frac{v+u\sin \alpha }{v^2-u^2}}$

La posición de encuentro es

${\displaystyle \{\begin{array}{l}{\xi }_t=y_t\cos \alpha =h\frac{n\left(1+n\sin \alpha \right)\cos \alpha }{1-n^2}\\ {\eta }_t=h+y_t\sin \alpha =h+h\frac{n\left(1+n\sin \alpha \right)\sin \alpha }{1-n^2}\end{array}}$

Ejemplos

• Sea n=0.5, α=π/4 (45°) y h=10

El torpedo alcanza al submarino, (u<v)

n=0.5; %cociente n=u/v
alfa=pi/4; %ángulo
h=10; %posición de partida del submarino

xx=linspace(0,h*cos(alfa),100);
y=@(x) h*n*(1+n*sin(alfa))/(1-n^2)+h*((1-sin(alfa))*(x/(h*cos(alfa)))
.^(1+n)/(1+n)-(1+sin(alfa))*(x/(h*cos(alfa))).^(1-n)/(1-n))/2;
xi=@(x) y(x)*cos(alfa)+x*sin(alfa);
eta=@(x) h+y(x)*sin(alfa)-x*cos(alfa);

hold on
plot(xi(xx),eta(xx))
T=h*(1+n*sin(alfa))/(1-n^2); %tiempo
fplot(@(t) n*cos(alfa)*t, @(t) h+n*sin(alfa)*t,[0,T])
yt=h*n*(1+n*sin(alfa))/(1-n^2); %encuentro
xi_t=yt*cos(alfa);
eta_t=h+yt*sin(alfa);
plot(xi_t,eta_t,'ro','markersize',4,'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('y')
title('Trayectoria del torpedo y submarino')



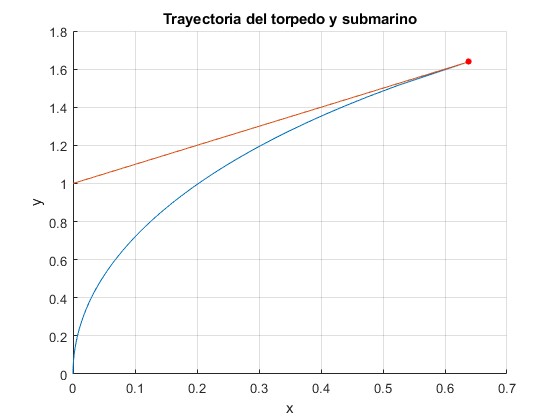
El tiempo T=1.805 que tarda en alcanzar el torpedo al submarino

>> T
T =    1.8047

• Sea n=0.5, α=0 (horizontal) y h=1

Reproducimos el primer ejemplo del apartado anterior 'Movimiento rectilíneo horizontal'

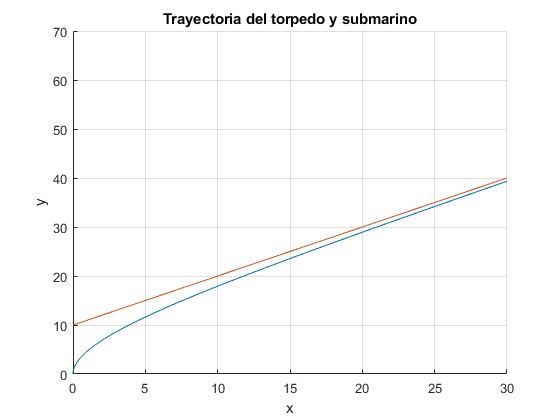
• Sea n=1.5, α=π/4 (45°) y h=10

El torpedo no alcanza al submarino, (u>v)

n=1.5; %cociente n=u/v
alfa=pi/4; %ángulo
h=10; %posición de partida del submarino

xx=linspace(0,h*cos(alfa),100);
y=@(x) h*n*(1+n*sin(alfa))/(1-n^2)+h*((1-sin(alfa))*(x/(h*cos(alfa))).
^(1+n)/(1+n)-(1+sin(alfa))*(x/(h*cos(alfa))).^(1-n)/(1-n))/2;
xi=@(x) y(x)*cos(alfa)+x*sin(alfa);
eta=@(x) h+y(x)*sin(alfa)-x*cos(alfa);

hold on
plot(xi(xx),eta(xx))
fplot(@(t) n*cos(alfa)*t, @(t) h+n*sin(alfa)*t,[0,50])
hold off
grid on
xlabel('x')
xlim([0,30])
ylabel('y')
title('Trayectoria del torpedo y submarino')



• Las velocidades del torpedo v y del submarino u son iguales, u=v, n=1

${\displaystyle \begin{array}{l}{\displaystyle \underset{y_0}{\overset{y}{\int }}dy}=\frac{1}{2}{\displaystyle \underset{x_0}{\overset{x}{\int }}\left\{\frac{x}{x_c}-\frac{x_c}{x}\right\}dx}\\ y-y_0=\frac{1}{2}\left\{\frac{1}{2}\frac{x^2-x_0^2}{x_c}-x_c\ln \left(\frac{x}{x_0}\right)\right\}\end{array}}$

donde

${\displaystyle x_c=\left(\frac{\cos \alpha }{1-\sin \alpha }\right)h\cos \alpha =\frac{h{\cos }^2\alpha }{1-\sin \alpha }=h\left(1+\sin \alpha \right)}$

El resultado es

${\displaystyle y=-\frac{h}{4}-\frac{3}{4}h\sin \alpha +\frac{1}{2}\left\{\frac{1}{2}\frac{x^2}{h\left(1+\sin \alpha \right)}-h\left(1+\sin \alpha \right)\ln \left(\frac{x}{h\cos \alpha }\right)\right\}}$

Ejemplo

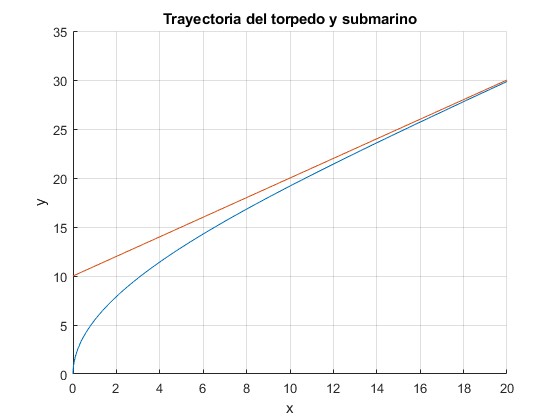
Sea n=1, α=π/4 (45°) y h=10

El torpedo no alcanza al submarino, (u=v)

n=1; %las velocidades u=v
alfa=pi/4; %ángulo
h=10; %posición de partida del submarino
xx=linspace(0,h*cos(alfa),100);
y=@(x) -h/4-3*h*sin(alfa)/4+(x.^2/(2*h*(1+sin(alfa)))-h*(1+sin(alfa))
*log(x/(h*cos(alfa))))/2;
xi=@(x) y(x)*cos(alfa)+x*sin(alfa);
eta=@(x) h+y(x)*sin(alfa)-x*cos(alfa);

hold on
plot(xi(xx),eta(xx))
fplot(@(t) n*cos(alfa)*t, @(t) h+n*sin(alfa)*t,[0,30])
hold off
grid on
xlabel('x')
xlim([0,20])
ylabel('y')
title('Trayectoria del torpedo y submarino')

Otra solución a este problema

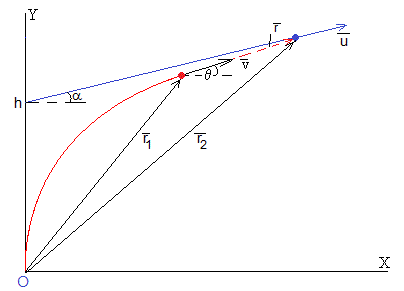
Sea $\overrightarrow{r_1}$ la posición del submarino, su posición inicial en el instante t=0, es $\overrightarrow{r_1}=h\widehat{j}$, su vector velocidad $\overrightarrow{u}=u\cos \alpha \widehat{i}+u\sin \alpha \widehat{j}$ contante en módulo y dirección, $\frac{d\overrightarrow{u}}{dt}=0$

Sea $\overrightarrow{r_2}$ la posición del torpedo, su posición inicial es el origen $\overrightarrow{r_2}=0$. Su vector velocidad $\overrightarrow{v}$ es constante en módulo pero no en dirección θ. Supondremos que v>u.

Su aceleración tangencial es nula (módulo constante), pero no lo es su aceleración normal, de modo que el vector velocidad $\overrightarrow{v}$ y el vector aceleración $\frac{d\overrightarrow{v}}{dt}$ son perpendiculares

Sea $\overrightarrow{r}=\overrightarrow{r_1}-\overrightarrow{r_2}$ la posición relativa. El vector posición relativa $\overrightarrow{r}$ tiene la misma dirección que el vector velocidad $\overrightarrow{v}$ del torpedo, de modo que el producto escalar $\overrightarrow{r}\frac{d\overrightarrow{v}}{dt}=0$

Evaluamos la derivada respecto del tiempo de $\overrightarrow{r}\left(\overrightarrow{u}+\overrightarrow{v}\right)$

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\overrightarrow{r}\left(\overrightarrow{u}+\overrightarrow{v}\right)\right)=\frac{d\left({\overrightarrow{r}}_1-\overrightarrow{r_2}\right)}{dt}\left(\overrightarrow{u}+\overrightarrow{v}\right)+\overrightarrow{r}\frac{d\left(\overrightarrow{u}+\overrightarrow{v}\right)}{dt}=\left(\overrightarrow{u}-\overrightarrow{v}\right)\left(\overrightarrow{u}+\overrightarrow{v}\right)+\overrightarrow{r}\left(\frac{d\overrightarrow{u}}{dt}+\frac{d\overrightarrow{v}}{dt}\right)=\\ u^2-v^2+\overrightarrow{r}\frac{d\overrightarrow{v}}{dt}=u^2-v^2\end{array}}$

La derivada con respecto del tiempo es constante. Integrando

${\displaystyle \overrightarrow{r}\left(\overrightarrow{u}+\overrightarrow{v}\right)=\left(u^2-v^2\right)t+c}$

donde c es una constante a determinar a partir de las condiciones iniciales. En el instante t=0

${\displaystyle {\overrightarrow{r}\left(\overrightarrow{u}+\overrightarrow{v}\right)|}_{t=0}=h\widehat{j}\left(u\cos \alpha \widehat{i}+u\sin \alpha \widehat{j}+v\widehat{j}\right)=h\left(u\sin \alpha +v\right)=\left(u^2-v^2\right)0+c}$

En el instante T, el torpedo alcanza al submarino, $\overrightarrow{r_1}=\overrightarrow{r_2},\overrightarrow{r}=\overrightarrow{r_1}-\overrightarrow{r_2}=0$, la posición relativa es nula

${\displaystyle \begin{array}{l}0=\left(u^2-v^2\right)T+h\left(u\sin \alpha +v\right)\\ T=\frac{h\left(u\sin \alpha +v\right)}{v^2-u^2}\end{array}}$

Que es el resultado que hemos obtenido en el apartado anterior. El submarino se habrá desplazado s=uT hasta que es alcanzado por el torpedo

${\displaystyle s=uT=h\frac{\frac{u}{v}\left(\frac{u}{v}\sin \alpha +1\right)}{1-\frac{u^2}{v^2}},u<v}$

Polígono

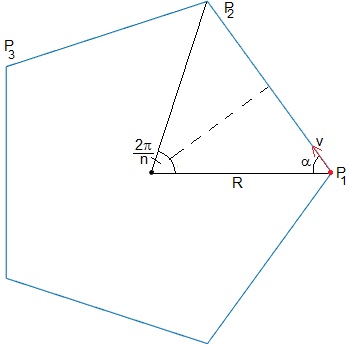
Consideremos un polígono regular de n≥3 lados. El vértice P_i persigue al vértice P_i+1, 1≤i<n, el vértice P_n persigue al P₁ con velocidad constante v.

En la figura, se muestra la situación inicial, la distancia de un vértice al centro es R, el ángulo entre dos vértices consecutivos es 2π/n. El vector velocidad hace con la dirección radial un ángulo α=π/2-π/n, tal como se aprecia en la figura.

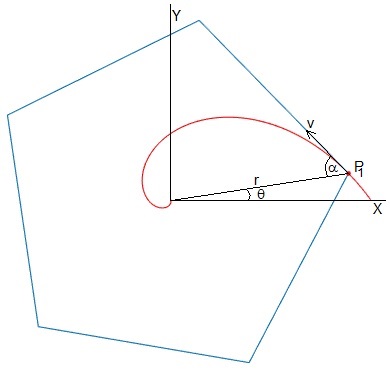
La componente radial de la velocidad es v·cosα. En el instante t el vértice se encuentra a una distancia r=R-vcosα·t del origen

Como la velocuidad es constante, el vértice llega al origen (desaparaece el polígono) en el instante T=R/(v·cosα)

La velocidad angular del vértice en el instante t es

${\displaystyle \begin{array}{l}\frac{d\theta }{dt}=\frac{v\sin \alpha }{r}\\ \frac{d\theta }{dt}=\frac{v\sin \alpha }{R-v\cos \alpha ·t}\end{array}}$

Integramos la ecuación diferencial entre el instante t=0 y t

${\displaystyle \begin{array}{l}\theta -{\theta }_0=\tan \alpha {\displaystyle \underset{0}{\overset{t}{\int }}\frac{dt}{\frac{R}{v\cos \alpha }-t}}=-\tan \alpha {\displaystyle \underset{0}{\overset{t}{\int }}\frac{dt}{t-\frac{R}{v\cos \alpha }}}\\ \theta -{\theta }_0={-\tan \alpha ·\ln \left(t-\frac{R}{v\cos \alpha }\right)|}_0^t=-\tan \left(\frac{\pi }{2}-\frac{\pi }{n}\right)·\ln \left(1-\frac{v\cos \alpha }{R}t\right)\\ \theta ={\theta }_0-\frac{\ln \left(\frac{r}{R}\right)}{\tan \left(\frac{\pi }{n}\right)}\end{array}}$

El primer vértice P₁, parte del eje X, θ₀=0, el segundo vértice parte de θ₀=2π/n, el tercer vértice de θ₀=4π/n y así, sucesivamente

El código MATLAB para dibujar parte de la figura es

n=5; %número de lados
R=1; %radio
hold on
r=linspace(0,1,100);
f=@ (x) -log(x/R)/tan(pi/n);
x=r.*cos(f(r));
y=r.*sin(f(r));
plot(x,y,'r')
r=0.9;
th=f(r);
for k=1:n
    line([r*cos(k*2*pi/n+th), r*cos((k-1)*2*pi/n+th)],
[r*sin(k*2*pi/n+th),r*sin((k-1)*2*pi/n+th)]);
end
plot(r*cos(th),r*sin(th),'ro','markersize',3,'markerfacecolor','r')
hold off
axis equal
axis off

Actividades

Se introduce

• El número n de lados del polígono regular.
• Se ha fijado la velocidad v=1 y el radio R=1

Se pulsa el botón titulado Nuevo.

Se observa la trayectoria (en color rojo) de cada uno de los vértices.

Movimiento circular

Problema sencillo

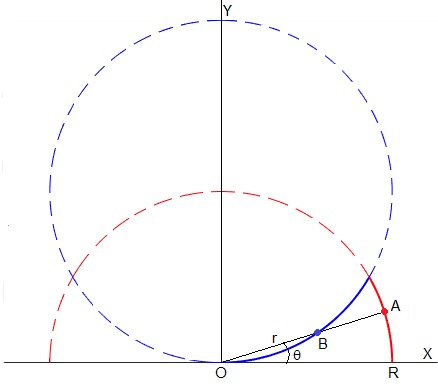
El móvil B parte del origen con velocidad constante v_B y el móvil A parte de la posición (R,0) moviéndose con velocidad constante v_A<v_B o con velocidad angular ω=v_A/R

La posición angular θ de cada uno de los móviles es

${\displaystyle \begin{array}{l}\frac{d\theta }{dt}=\frac{v_A}{R}\\ \theta =\frac{v_A}{R}t\end{array}}$

La distancia r al origen del móvil B es

${\displaystyle \begin{array}{l}{v}_B^2={\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{d\theta }{dt}\right)}^2={\left(\frac{dr}{dt}\right)}^2+r^2{\left(\frac{v_A}{R}\right)}^2\\ \frac{dr}{dt}=\sqrt{v_B^2-{\left(\frac{v_A}{R}\right)}^2{r}^2}\end{array}}$

Integramos, con la condición inicial, en el instante t=0, el móvil B parte del origen

${\displaystyle \begin{array}{l}\frac{R}{v_A}{\displaystyle \underset{0}{\overset{r}{\int }}\frac{dr}{\sqrt{{\left(\frac{v_B}{v_A}R\right)}^2-r^2}}}={\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ {\frac{R}{v_A}\arcsin \left(\frac{v_A}{v_B}\frac{r}{R}\right)|}_0^r=t\\ \arcsin \left(\frac{v_A}{v_B}\frac{r}{R}\right)=\frac{v_A}{R}t\\ \frac{r}{R}=\frac{v_B}{v_A}\sin \left(\frac{v_A}{R}t\right)\\ r=R\frac{v_B}{v_A}\sin \theta \end{array}}$

Esta es la ecuación de la trayectoria del móvil B

Los móviles se encuentran cuando r=R, en la posición angular

${\displaystyle {\theta }_e=\arcsin \left(\frac{v_A}{v_B}\right)}$

Lo que requiere que v_A<v_B

El código MATLAB para dibujar parte de la figura es

R=1; %radio
vA=1;
vB=2;
hold on
fplot(@(t) R*cos(t), @(t) R*sin(t),[0,pi],'color','r')
th_e=asin(vA/vB);
r=@(th) R*vB*sin(th)/vA;
fplot(@(th) r(th).*cos(th), @(th) r(th).*sin(th), [0,2*pi], 'color','b')
fplot(@(th) r(th).*cos(th), @(th) r(th).*sin(th), [0,th_e],'color','b',
'lineWidth',1.5)
fplot(@(t) R*cos(t), @(t) R*sin(t),[0,th_e],'color','r','lineWidth',1.5)

hold off
axis equal

Problema más complicado

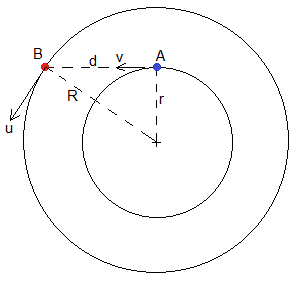
Sean dos móviles A (cazador) y B (presa)

El móvil B describe un movimiento circular de radio R con velocidad constante u.

El móvil A parte de una posición inicial y se mueve hacia B con velocidad constante v. La dirección de dicha velocidad es la línea que une A y B.

Después de un tiempo, el móvil A se mueve en una circunferencia de radio r con la misma velocidad angular que B

${\displaystyle \frac{u}{R}=\frac{v}{r},r=\frac{v}{u}R}$

La distancia d entre los dos móviles es

${\displaystyle d=\sqrt{R^2-r^2}=R\sqrt{1-\frac{v^2}{u^2}}}$

Ejemplo 1

• Velocidad de B, u=2
• Velocidad de A, v=1
• Radio de la trayectoria circular de B, R=1
• Posición inicial de B, (R,0)
• Posición inicial de A, (1.5,0)

u=2; %velocidad de B
v=1; %velocidad de A
dt=0.01; %intervalo de tiempo
R=1; %radio de B
tt=0:dt:10;
xA=zeros(1,length(tt));
yA=zeros(1,length(tt));
hold on
i=1;
xA(1)=1.5; %posición inicial de A
yA(1)=0;
%Trayectoria circular de B
fplot(@(th) R*cos(th), @(th) R*sin(th),[0,2*pi], 'b')
%posición inicial de A y B
plot(xA(1),yA(1),'ro','markersize',4,'markerfacecolor','r')
plot(R,0,'bo','markersize',4,'markerfacecolor','b')
%trayectoria de A
for t=tt
	xB=R*cos(u*t/R);
	yB=R*sin(u*t/R);
	distancia=sqrt((xA(i)-xB)^2+(yA(i)-yB)^2);
	vx=v*(xB-xA(i))/distancia;
	vy=v*(yB-yA(i))/distancia;
	xA(i+1)=xA(i)+vx*dt;
	yA(i+1)=yA(i)+vy*dt;
        i=i+1;
end
plot(xA,yA, 'r')
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Trayectorias')

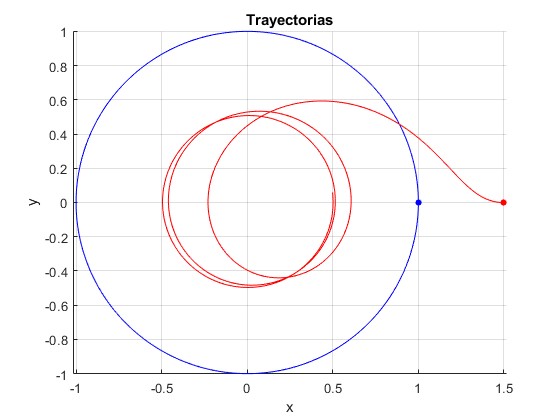
El punto de color rojo, muestra la posición inicial de A, el azul la posición inicial de B

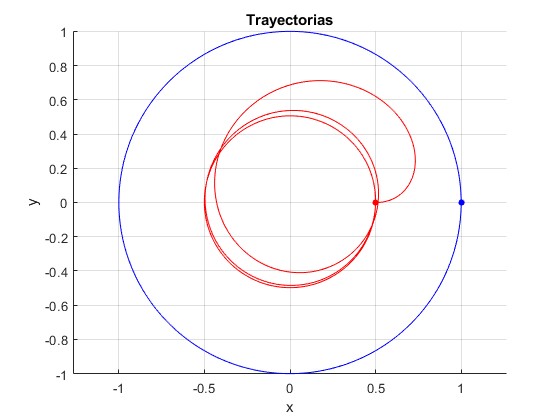
Cambiamos la posición inicial de A a (0.5,0)

Ejemplo 2

• Velocidad de B, u=0.95
• Velocidad de A, v=1
• Radio de la trayectoria circular de B, R=1
• Posición inicial de B, (R,0)
• Posición inicial de A, (1.5,0)

Se define la posición de encuentro cuando la distancia entre A y B es menor que 0.001

u=0.95; %velocidad de B
v=1; %velocidad de A
dt=0.01; %intervalo de tiempo
R=1; %radio de B
tt=0:dt:10;
xA=zeros(1,length(tt));
yA=zeros(1,length(tt));
hold on
i=1;
xA(1)=1.5; %posición inicial de A
yA(1)=0;
%Trayectoria circular de B
fplot(@(th) R*cos(th), @(th) R*sin(th),[0,2*pi], 'b')
%posición inicial de A y B
plot(xA(1),yA(1),'ro','markersize',4,'markerfacecolor','r')
plot(R,0,'bo','markersize',4,'markerfacecolor','b')
%trayectoria de A
for t=tt
	xB=R*cos(u*t/R);
	yB=R*sin(u*t/R);
	distancia=sqrt((xA(i)-xB)^2+(yA(i)-yB)^2);
        if distancia<0.001
           break;
        end
	vx=v*(xB-xA(i))/distancia;
	vy=v*(yB-yA(i))/distancia;
	xA(i+1)=xA(i)+vx*dt;
	yA(i+1)=yA(i)+vy*dt;
       i=i+1;
end
xA(i+1:end)=[];
yA(i+1:end)=[];
plot(xA,yA, 'r')
plot(xA(end),yA(end),'ko','markersize',4,'markerfacecolor','k') %encuentro
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Trayectorias')

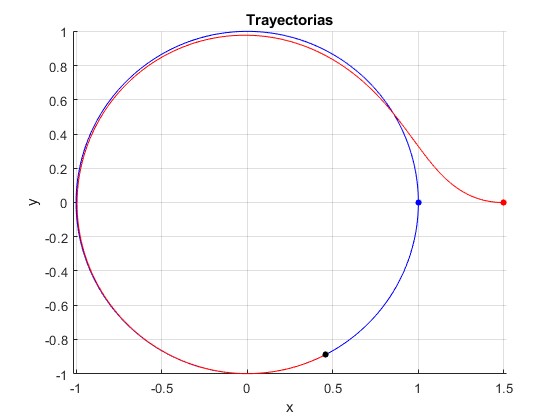
El punto de color rojo, muestra la posición inicial de A, el azul la posición inicial de B, el de color negro, la posición de encuentro

Cambiamos la posición inicial de A a (0.5,0)

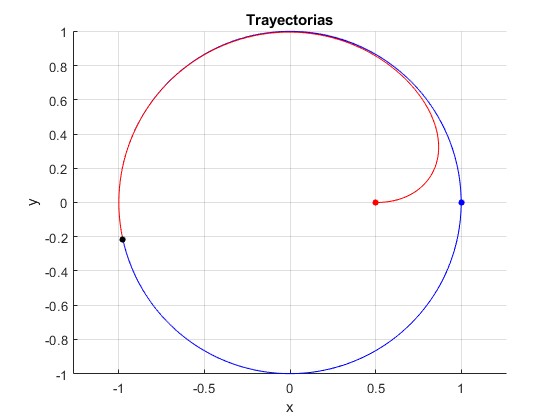
Actividades

Se introduce

• La velocidad v del móvil A, en el control titulada Velocidad.
• La velocidad de B se ha fijado en u=1
• La posición inicial de A es aleatoria

Se pulsa el botón titulado Nuevo.

Se observa la trayectoria circular de A (en color rojo) y la trayectoria de B (en color azul).

La flecha de color azul, representa la velocidad de B, su dirección es la recta que pasa por B y A.

Se proporcionan los datos de

• El tiempo t
• La distancia d entre A y B

Referencias

Mungan C. E., A classic chase problem solved from a physics perspective. Eur. J. Phys. 26 (2005), pp. 985-990

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017

Atsushi Kamimura, Toru Ohira. Group Chase and Escape. Fusion of Pursuits-Escapes and Collective Motions. Spinger 2019. pp. 10-16

Yuan Qing-Xin, Du Yin-Xiao. Note on the dog-and-rabbit chase problem in introductory kinematics. Eur. J. Phys. 29 (2008) N43–N45.
Z K Silagadze, G I Tarantsev. Comment on ‘Note on the dog-and-rabbit chase problem in introductory kinematics’. Eur. J. Phys. 31 (2010), L37–L38

Felipe Costa Melo Cunha, Rudini Sampaio. Revisitando dois problemas clássicos do Irodov sobre curvas de perseguição. Revista Brasileira de Ensino de Física, vol. 46, e20230307 (2024)

Physics Challenge for Teachers and Students. Solution to October 2016 Challenge. A big spider chase. The Physics Teacher. Vol. 54, 2016, pp. 472