Choques en un carril

Supongamos dos partículas de masas m₁ y m₂ que llevan la misma velocidad v₀ y se dirigen al final del carril, tal como se muestra en la figura.

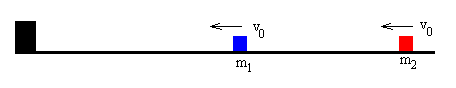
Descripción

Choque con el extremo del carril

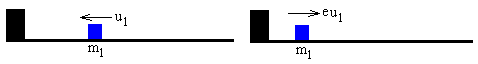
Cuando la partícula de masa m₁ que lleva una velocidad u₁ choca con el final del carril cambia el sentido y el módulo de su velocidad a v₁=-eu₁, siendo e el coeficiente de restitución.

Choque de las dos partículas

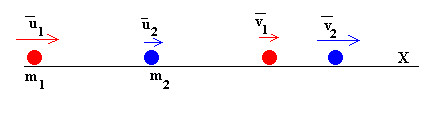
Aplicamos el principio de conservación del momento lineal

m₁u₁+m₂u₂=m₁v₁+m₂v₂

y de la definición del coeficiente de restitución e

-e(u₁-u₂)=v₁-v₂

Despejamos las velocidades después del choque v₁ y v₂

$v_{1} = \frac{(m_{1} - m_{2} e) u_{1} + m_{2} (1 + e) u_{2}}{m_{1} + m_{2}} v_{2} = \frac{m_{1} (1 + e) u_{1} + (m_{2} - m_{1} e) u_{2}}{m_{1} + m_{2}}$

Movimiento de las partículas

La partícula de masa m₁ se dirige hacia el extremo del carril con velocidad -v₀, choca y cambia su velocidad a ev₀

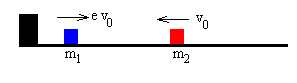
Posteriormente chocan las dos partículas con velocidades iniciales u₁=ev₀ y u₂=-v₀

$v_{1} = \frac{e m_{1} - m_{2} (e^{2} + e + 1)}{m_{1} + m_{2}} v_{0} v_{2} = \frac{m_{1} (2 + e) e - m_{2}}{m_{1} + m_{2}} v_{0}$

La masa m₁ permanece en reposo v₁=0 después del choque si

m₁=m₂(e²+e+1)/e

Si el choque es elástico e=1, m₁=3m₂, v₂=2v₀. Toda la energía inicial se transfiere a la partícula de masa m₂.

Si el choque no es elástico, por ejemplo e=0.8, m₁=3.05m₂, v₂=1.44v₀

Si m₁<3m₂, la partícula de masa m₁ choca una segunda vez con el final del carril. Se aproxima a la partícula m₂ con velocidad -ev₁

Si -ev₁<v₂ no hay más colisiones
Si -ev₁>v₂, entonces m₁ chocará con m₂ una segunda vez, siempre que m₁<m₂

Las velocidades de las dos partículas después de esta segunda colisión con u₁=-ev₁ y u₂=v₂ es

$\begin{array}{l} v_{3} = \frac{- (m_{1} - m_{2} e) e v_{1} + m_{2} (1 + e) v_{2}}{m_{1} + m_{2}} = \frac{m_{1} m_{2} (3 e^{3} + 4 e^{2} + 3 e) - m_{1}^{2} e^{2} - m_{2}^{2} (e^{4} + e^{3} + e^{2} + e + 1)}{{(m_{1} + m_{2})}^{2}} v_{0} \\ v_{4} = \frac{- m_{1} (1 + e) e v_{1} + (m_{2} - m_{1} e) v_{2}}{m_{1} + m_{2}} = \frac{m_{1} m_{2} (e^{4} + 2 e^{3} + 3 e^{2} + 4 e) - m_{1}^{2} (2 e^{3} + 3 e^{2}) - m_{2}^{2}}{{(m_{1} + m_{2})}^{2}} v_{0} \end{array}$

Cuando e=1, la partícula de masa m₁ permanecerá en reposo tras la segunda colisión si m₁=0.528 m₂

Cuando m₁ es pequeña frente a m₂, puede experimentar múltiples colisiones con el final del carril y con m₂.

Ejemplo:

Masas de las partículas

m₁=0.5 kg

m₂=1.0 kg

Velocidades iniciales

u₁=-1.0 m/s

u₂=-1.0 m/s

Coeficiente de restitución

e=0.8

La partícula m₁ choca con el final del carril y rebota con velocidad

v₁=-eu₁=0.8 m/s

Esta es la velocidad inicial u₁=0.8 de la partícula m₁ cuando choca con la partícula m₂

Las velocidades después del primer choque son:

$\begin{array}{l} v_{1} = \frac{(0.5 - 1.0 \cdot 0.8) 0.8 + 1.0 (1 + 0.8) (- 1.0)}{0.5 + 1.0} = - 1.36 \\ v_{2} = \frac{0.5 (1 + 0.8) 0.8 + (1.0 - 0.5 \cdot 0.8) (- 1.0)}{0.5 + 1.0} = 0.08 \end{array}$

La partícula m₁ se dirige hacia el final del carril y rebota con velocidad u₁=-ev₁=1.088 m/s

La partícula m₁ choca por segunda vez con la partícula m₂ cuya velocidad inicial u₂=0.08 m/s

$\begin{array}{l} v_{1} = \frac{(0.5 - 1.0 \cdot 0.8) 1.088 + 1.0 (1 + 0.8) 0.08}{0.5 + 1.0} = - 0.1216 \\ v_{2} = \frac{0.5 (1 + 0.8) 1.088 + (1.0 - 0.5 \cdot 0.8) 0.08}{0.5 + 1.0} = 0.6848 \end{array}$

La partícula m₁ se dirige hacia el final del carril y rebota con velocidad u₁=-ev₁=0.0973m/s

Ahora, ambas partículas se dirigen a lo largo del eje X hacia la derecha, la velocidad de m₁ (0.0973) es menor que la velocidad de m₂ (0.6848) por lo que ya no hay más choques. Estas son las velocidades finales de las dos partículas.

La energía inicial y final del sistema formado por las dos partículas es

$\begin{array}{l} E_{i} = \frac{1}{2} m_{1} u_{1}^{2} + \frac{1}{2} m_{2} u_{2}^{2} \\ E_{i} = \frac{1}{2} 0.5 \cdot {1.0}^{2} + \frac{1}{2} 1.0 \cdot {1.0}^{2} = 0.75 J \\ E_{f} = \frac{1}{2} 0.5 \cdot {0.0973}^{2} + \frac{1}{2} 1.0 \cdot 6848^{2} = 0.24 J \end{array}$

Se ha perdido energía en los sucesivos choques entre las partículas y de la primera con el final del carril.

Actividades

Se introduce

El cociente m₁/m₂ de las masas de las dos partículas, actuando en la barra de desplazamiento titulada Cociente m1/m2
El coeficiente de restitución e, actuando en la barra de desplazamiento titulada Coef. Restitución
La velocidad inicial de las dos partículas se ha fijado en u₁=-1.0 m/s y u₂=-1.0 m/s
Se pulsa el botón titulado Empieza

Observamos los choques de la primera partícula contra el final del carril, y el choque entre las dos partículas.

Los datos de las velocidades de las dos partículas aparecen en la parte superior del applet.

Una barra dividida nos indica:

La energía cinética de la primera partícula (en color azul)
La energía cinética de la segunda partícula (en color rojo)
El resto hasta completar la barra es la energía perdida en los choques.

Cuando el choque es elástico, e=1, la energía inicial es igual a la final.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Cross R., Vertical bounce of two vertically aligned balls. Am. J. Phys. 75 (11) November 2007, pp 1009-1016