Choques frontales verticales
En esta página, se describe un ejemplo interesante de choques frontales.
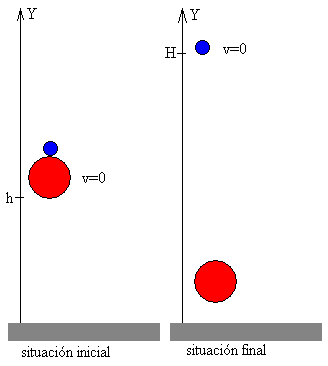 Hemos comprobado en la página “Caída libre y sucesivos
rebotes” que cuando una pelota se deja caer desde una altura h0,
rebota en el suelo y alcanza una altura máxima h<h0. La
relación entre estas alturas es
Hemos comprobado en la página “Caída libre y sucesivos
rebotes” que cuando una pelota se deja caer desde una altura h0,
rebota en el suelo y alcanza una altura máxima h<h0. La
relación entre estas alturas es
h=e2·h0
donde e es el coeficiente de restitución e≤1.
Vamos a comprobar que cuando una pequeña pelota se coloca encima de otra pelota mayor y se dejan caer juntas desde una altura h0, la pelota pequeña puede alcanzar alturas mucho mayores que h0.
Choques verticales de dos pelotas
Supondremos que las dos pelotas se comportan como masas puntuales, es decir, que sus dimensiones son pequeñas comparadas con la altura h0 desde la que dejan caer.
Vamos a describir en este apartado cada una de las etapas del movimiento de las dos pelotas:
- Movimiento vertical de caída
Si ambas pelotas parten del reposo desde una altura h0, las ecuaciones del movimiento son
Las pelotas llegan al suelo cuando y=0, es decir con una velocidad –v0 tal que
- Choque de la pelota grande con el suelo
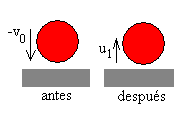
La pelota grande choca con el suelo y rebota . De la definición de coeficiente de restitución, tendremos que la velocidad u1 de la pelota grande después del choque es
u1=e1v0
Siendo e1 el coeficiente de
restitución para el choque entre la pelota grande y el suelo.
- Choque de la pelota grande con la pequeña
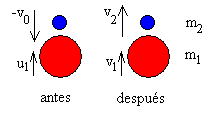 Tenemos que plantear las ecuaciones que describen el choque frontal entre dos partículas, una partícula (la pelota grande) de masa m1 que lleva una velocidad u1 hacia arriba, y otra partícula
(la pelota pequeña) de masa m2 que lleva una velocidad u2=-v0 hacia abajo, tal como se muestra en
la figura.
Tenemos que plantear las ecuaciones que describen el choque frontal entre dos partículas, una partícula (la pelota grande) de masa m1 que lleva una velocidad u1 hacia arriba, y otra partícula
(la pelota pequeña) de masa m2 que lleva una velocidad u2=-v0 hacia abajo, tal como se muestra en
la figura.
Para calcular las velocidades v1 y v2 después del choque aplicamos:
- el principio de conservación del momento lineal
m1·u1+m2(-v0)=m1·v1+m2·v2
- y la definición de coeficiente de restitución
v1-v2=-e2(u1-(-v0))
Siendo e2 el coeficiente de restitución para el choque entre la pelota grande y la pequeña.
Para hacer más simple el análisis del problema supondremos que los coeficientes de restitución e1≈e2=e son prácticamente iguales.
m1ev0-m2v0=m1·v1+m2·v2
v1-v2=-e(ev0+v0)Despejamos de este sistema de dos ecuaciones las velocidades v1 y v2 después del choque
- Movimiento vertical ascendente
La pelota más grande asciende desde el suelo con velocidad inicial v1 y la pelota pequeña con velocidad inicial v2, las ecuaciones del movimiento para la primera son
La máxima altura se alcanza cuando v=0.
La misma expresión se obtiene para la pelota pequeña
Casos particulares
- Condición para que la pelota grande permanezca en reposo, v1=0
En el caso de un choque elástico e=1, la velocidad v1=0 se obtiene para m1=3m2. La pelota grande permanece en reposo sobre el suelo, cuando la masa de la pelota grande es el triple que el de la pequeña. La velocidad de la pelota pequeña es v2=2v0. La máxima altura que alcanza la pelota pequeña es por tanto, h2=4h0
En general, para que la pelota pequeña ascienda hasta una altura h2>h0 se tendrá que cumplirse que v2>v0, y ascenderá a la altura mayor posible si v1=0, la pelota grande queda en reposo sobre el suelo.
Poniendo en la segunda ecuación (definición de coeficiente de restitución) que describe el choque frontal v1=0, para que v2>v0 se tiene que cumplir que e2+e-1>0, es decir, e>0.618.
Para que la pelota grande permanezca en reposo en el suelo, v1=0, la relación de masas m1/m2 para cualquier valor de e>0.618, deberá cumplir
Para un valor típico e=0.9, m1=3.011·m2, la masa de la pelota grande m1 es un poco más de tres veces la masa de la pelota pequeña. La velocidad de la pelota pequeña v2=1.71v0, y por tanto, h2=2.92·h0
- Cuando la masa de la pelota pequeña es despreciable
Cuando la masa de la pelota pequeña es despreciable m2<<m1, para las colisiones elásticas e=1 se obtiene v2≈3·v0, De modo que, la altura que alcanza la pelota pequeña es h2≈9·h0.
Balance energético
-
La energía inicial de las partículas cuando están a una altura h0 sobre el suelo es
Ei=(m1+m2)gh0
-
La pelota más grande rebota contra el suelo y pierde una energía Q1 en el choque. La velocidad inicial es v0 y la velocidad final e·v0.
-
La pelota más pequeña llega al suelo con velocidad v0 y choca con la pelota grande que ha rebotado llevando una velocidad ev0. Durante el choque se pierde una energía,
-
El resto de la energía Ef=Ei+Q1+Q2 se convierte en energía cinética de las dos partículas que ascienden con velocidades v1 y v2 respectivamente.
-
Posteriormente, esta energía cinética se convierte en potencial cuando alcanzan las alturas máximas h1 y h2 respectivamente.
Si la pelota mayor queda en reposo sobre el suelo, v1=0, la energía final Ef se convierte en energía potencial de pelota más pequeña cuando alcanza la altura máxima h2.
Ejemplo
Supongamos que e=0.9 y m1=3.011·m2, la altura inicial es h0=0.25 m
- Energía inicial Ei=4.011·9.8·0.25=9.83 J
- La velocidad de la pelota más grande al llegar al suelo es v0=2.21 m/s.
- Después de chocar con el suelo su velocidad es e·v0=1.99 m/s. La pérdida de energía durante el choque es Q1=-1.40 J
- La pelota más pequeña llega al suelo con velocidad v0=2.21 m/s y choca con la pelota grande después de rebotar. La pérdida de energía en el choque es Q2=-1.26 J
- La pelota grande permanece en reposo sobre le suelo. La energía de la pelota pequeña es Ef=9.83-1.40-1.26=7.16 J. La energía cinética de la pelota pequeña al nivel del suelo se convierte en energía potencial cuando alcanza la altura h2=0.73 m.
Actividades
Se introduce
- La masa m1 de la pelota grande, un número mayor que la unidad, en el control de edición titulado Masa grande.
- La masa de la pelota pequeña m2 se ha fijado en 1 kg.
- El coeficiente de restitución e, un número menor que 1.0 y mayor que 0.6, en el control de edición titulado Coef. restitución.
- La altura inicial h0, en cm, actuando en la barra de desplazamiento titulada Altura.
Se pulsa en el botón titulado Empieza
Por ejemplo
- masa grande, m2=200,
- coeficiente de restitución, e=1.0,
- altura inicial, h0=10 cm.
Observar que la pelota pequeña (de color azul) alcanza una altura máxima h2 cercana a los 90 cm
Introducir un valor para el coeficiente de restitución e, cambiar el valor de la masa m1 de la pelota grande hasta conseguir que después de chocar con la pelota pequeña, permanezca en reposo sobre el suelo.
-
A la izquierda del applet, observamos el movimiento vertical de la pelota grande (color rojo) y de la pelota pequeña (color azul).
-
En el centro, las barras indican la energía (cinética más potencial) de cada partícula y cómo se va trasformando.
-
A la derecha, se representa gráficamente, la velocidad de la pelota pequeña en función del tiempo.
Referencias
Spradley J. Velocity amplification in vertical collisions. Am. J. Phys. 55 (2) February 1987, pp. 183-184
