Choques verticales elásticos

En esta sección, vamos a estudiar los choques elásticos verticales entre dos y tres pequeñas pelotas y generalizaremos el resultado para el caso de n pelotas.

Dos pelotas

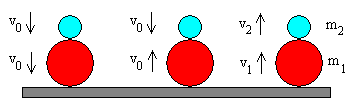
Las dos pelotas de masas m₁ (la inferior) y m₂ (superior) caen juntas desde una altura h₀, cuando llegan al suelo alcanzan la velocidad -v₀.
La pelota inferior de masa m₁ rebota elásticamente en el suelo invirtiendo el sentido de su velocidad.
La pelota inferior de masa m₁ y velocidad v₀ choca con la pelota superior de masa m₂ y velocidad –v₀. Las velocidades de las dos pelotas después del choque son v₁ y v₂.

Principio de conservación del momento lineal

m₁·v₀+m₂(-v₀)=m₁·v₁+m₂·v₂

Definición de coeficiente de restitución

v₁-v₂=-e(v₀-(-v₀))

Si el choque es elástico, e=1

v₁-v₂=-2v₀

Despejamos v₁ y v₂ del sistema de dos ecuaciones

$v_{1} = \frac{m_{1} - 3 m_{2}}{m_{1} + m_{2}} v_{0} v_{2} = \frac{3 m_{1} - m_{2}}{m_{1} + m_{2}} v_{0}$

Si m₁=m₂, v₂=v₀
Si m₁=3m₂, v₂=2v₀
Si m₁>>m₂ v₂=3v₀

La máxima altura que alcanza la pelota más ligera es h=9·h₀

Tres pelotas

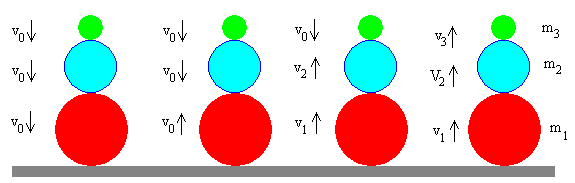
Las tres pelotas de masas m₁ (la inferior) y m₂ (intermedia) y m₃ (superior) caen juntas desde una altura h₀, cuando llegan al suelo alcanzan la velocidad -v₀.
La pelota inferior de masa m₁ rebota elásticamente en el suelo, invirtiendo el sentido de su velocidad.
La pelota inferior de masa m₁ y velocidad v₀ choca con la pelota intermedia de masa m₂ y velocidad –v₀. Las velocidades de las dos pelotas después del choque son v₁ y v₂.

Aplicando el conservación del momento lineal, y suponiendo que el choque es elástico

m₁·v₀+m₂(-v₀)=m₁·v₁+m₂·v₂v₁-v₂=-2v₀

Despejamos como antes, las velocidades v₁ y v₂ del sistema de dos ecuaciones

$v_{1} = \frac{m_{1} - 3 m_{2}}{m_{1} + m_{2}} v_{0} v_{2} = \frac{3 m_{1} - m_{2}}{m_{1} + m_{2}} v_{0}$

La pelota intermedia de masa m₂ y velocidad v₂ choca con la pelota superior de masa m₃ y velocidad –v₀. Las velocidades de las dos pelotas después del choque son V₂ y v₃.

Aplicando el conservación del momento lineal, y suponiendo que el choque es elástico

m₂·v₂+m₃(-v₀)=m₂·V₂+m₃·v₃V₂-v₃=-(v₂-(-v₀))

Despejamos como antes, las velocidades v₃ y V₂ del sistema de dos ecuaciones

$V_{2} = \frac{3 m_{1} m_{2} - m_{2}^{2} - 5 m_{1} m_{3} - m_{2} m_{3}}{(m_{1} + m_{2}) (m_{2} + m_{3})} v_{0} v_{3} = \frac{7 m_{1} m_{2} - m_{2}^{2} - m_{1} m_{3} - m_{2} m_{3}}{(m_{1} + m_{2}) (m_{2} + m_{3})} v_{0}$

Si m₁=m₂=m₃ entonces v₃=v₀
Si m₁>>m₂>>m₃ entonces v₃=7v₀

La máxima altura que alcanza la pelota más ligera es h=49·h₀

Cuatro pelotas

Si m₁>>m₂>>m₃>>m₄ entonces v₄=15v₀

La máxima altura que alcanza la pelota más ligera es h=225·h₀

n pelotas

Si m₁>>m₂…. >>m_n entonces v_n=(2ⁿ-1)v₀

Por ejemplo, si dejamos caer ocho pelotas desde un edificio muy alto de 100 m de altura, la velocidad al llegar al suelo es de

$v_{0} = \sqrt{2 \cdot 9.8 \cdot 100} = 44.3 m/s$

Si las masas de las pelotas cumplen la condición de que

m₁>>m₂>>… >>m₈

la velocidad de rebote de la octava pelota es v₈=(2⁸-1)v₀=11289.3 m/s

que es mayor que la velocidad de escape v_e de un objeto de la superficie de la Tierra

$v_{e} = \sqrt{\frac{2 G M}{R}} = 11191 m/s$

R=6370 km es el radio de la Tierra, M=5.98·10²⁴ kg es la masa de la Tierra y G=6.67·10^-11 N·m²/kg².

Referencias

Anderson A. The cocktail (highball) problem. Phys. Educ 34 (2) March 1999, pp. 76-79