Choques frontales elásticos en un carril

En esta página, vamos a estudiar de nuevo las colisiones elásticas de dos objetos que se mueven a lo largo de un carril sin rozamiento pero con un cambio que hace que el problema sea más interesante. Las partículas están obligadas a moverse en un carril de longitud L cuyos sus extremos reflejan perfectamente las partículas. Es decir, cuando una partícula llega al uno de los extremos del carril rebota y cambia el signo de su velocidad, pero no cambia su módulo.

En un carril finito, con extremos perfectamente reflectantes, las partículas experimentan sucesivos choques.

El interés del problema radica en investigar la posición de las partículas en el momento en el que ocurre cada uno de los choques. ¿Se observan regularidades?. ¿Cómo cambian si se modifica la relación entre las masas de las partículas o la posición inicial del primer choque?.

Descripción

En el instante t=0, las posiciones de las partículas de masas m_x y m_y son x₀ e y₀, (0≤x₀ < y₀<L) sus velocidades iniciales son u_x=u₀ y u_y=0, tal como se muestra en la figura.

Primer choque

En el instante t=(y₀-x₀)/u_x tiene lugar el choque elástico

Las velocidades de las partículas después del choque son:

$v_{x} = \frac{2 m_{y} u_{y} + (m_{x} - m_{y}) u_{x}}{m_{x} + m_{y}} v_{y} = \frac{2 m_{x} u_{x} + (m_{y} - m_{x}) u_{y}}{m_{x} + m_{y}}$

Después del choque puede ocurrir

Que las dos partículas se desplacen hacia la derecha v_x>0, v_y>0,
Que la partícula incidente se desplace hacia la izquierda v_x<0 y la segunda partícula se desplace hacia la derecha v_y>0

Ponemos el contador parcial de tiempos a cero para calcular la posición del segundo choque.

Segundo choque

Si las dos partículas se desplazan hacia la derecha después del choque v_x>0, v_y>0, la segunda se refleja en el extremo x=L, y choca con la primera.

En el instante t de encuentro

$x = y_{0} + v_{x} t y = L - v_{y} (t - \frac{L - y_{0}}{v_{y}})$

donde (L-y₀)/v_y es el tiempo que tarda la segunda partícula en reflejarse en el extremo x=L y cambiar el signo de la velocidad. El punto de encuentro se obtiene igualando x=y.

$t_{1} = 2 \frac{L - y_{0}}{v_{x} + v_{y}} x_{1} = y_{1} = \frac{2 L v_{x} + y_{0} (v_{y} - v_{x})}{v_{x} + v_{y}}$

Las velocidades iniciales antes del próximo choque son

u_x=v_x, u_y=-v_y

Si después del primer choque, la partícula incidente se desplaza hacia la izquierda v_x<0 y la segunda partícula se desplaza hacia la derecha v_y>0, pueden ocurrir tres casos:

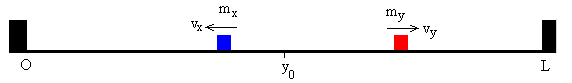
Que se reflejen las dos partículas en los extremos x=0 y x=L, respectivamente y a continuación, choquen.

$x = | v_{x} | (t - \frac{y_{0}}{| v_{x} |}) y = L - v_{y} (t - \frac{L - y_{0}}{v_{y}})$

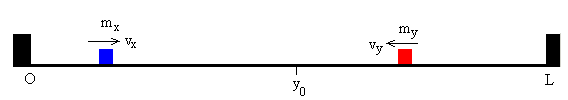
La posición del próximo choque es

$t_{1} = \frac{2 L}{| v_{x} | + v_{y}} x_{1} = y_{1} = \frac{2 L | v_{x} |}{| v_{x} | + v_{y}} - y_{0}$

Las velocidades de las partículas antes del próximo choque son

u_x=-v_x, u_y=-v_y

Que la segunda partícula se refleje en x=L y choque con la primera antes de alcanzar el extremo x=0.

$x = y_{0} - | v_{x} | t y = L - v_{y} (t - \frac{L - y_{0}}{v_{y}})$

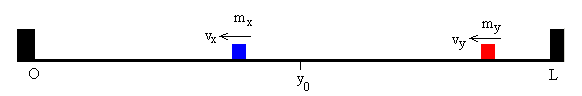
La posición del próximo choque es

$t_{1} = 2 \frac{L - y_{0}}{v_{y} - | v_{x} |} x_{1} = y_{1} = \frac{(| v_{x} | + v_{y}) y_{0} - 2 L | v_{x} |}{v_{y} - | v_{x} |}$

Las velocidades de las partículas antes del choque son

u_x=v_x, u_y=-v_y

Que la primera partícula se refleje en x=0 y choque con la segunda antes de alcanzar el extremo x=L.

$x = | v_{x} | (t - \frac{y_{0}}{| v_{x} |}) y = y_{0} + v_{y} t$

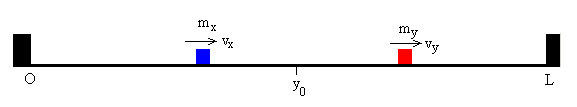
La posición del próximo choque es

$t_{1} = \frac{2 y_{0}}{| v_{x} | - v_{y}} x_{1} = y_{1} = \frac{| v_{x} | + v_{y}}{| v_{x} | - v_{y}} y_{0}$

Las velocidades de las partículas antes del choque son

u_x=-v_x, u_y=v_y

Conocidas las velocidades iniciales u_x y u_y antes del segundo choque, en la posición x₁=y₁ se calcula las velocidades de las dos partículas v_x y v_y después del choque. Un razonamiento similar al empleado a lo largo de este apartado, nos conduce a predecir la posición del tercer choque y así, sucesivamente

Ejemplo:

Masa de las partículas m_x=1.0, m_y=1.25
Longitud del carril, L=1.0
En el instante t=0, las partículas parten de la posiciones x₀=1.0, y₀=0.5
Velocidad de las partículas: u_x=1.0, u_y=0.0

Primer choque

En el instante t=(y₀-x₀)/u_x=0.4 s tiene lugar el primer choque en la posición y₀=0.5

Las velocidades de las partículas después del choque son:

$v_{x} = \frac{2 m_{y} u_{y} + (m_{x} - m_{y}) u_{x}}{m_{x} + m_{y}} = - 0 .111 v_{y} = \frac{2 m_{x} u_{x} + (m_{y} - m_{x}) u_{y}}{m_{x} + m_{y}} = 0 .889$

La partícula incidente se desplaza hacia la izquierda y la segunda partícula se desplaza hacia la derecha. Como la velocidad de la primera partícula es pequeña y la de la segunda es grande, la segunda rebotará en el extremo derecho del carril x=1.0 y alcanzará a la primera antes de que rebote en el extremo izquierdo x=0.

La ecuación del movimiento de las partículas son:

x=0.5-0.111·t
y=1.0-0.889·(t-0.5/0.889)

Igualando x=y, se obtiene el instante y la posición del segundo choque

x₁=y₁=0.357

Las velocidades de las partículas antes del segundo choque son:

u_x=-0.111, u_y=-0.889

Segundo choque

Las velocidades de las partículas después del choque son:

v_x=-0.975, v_y=-0.198

Las dos partículas se mueven hacia la izquierda. La primera partícula se refleja en el extremo izquierdo del carril, x=0, y choca con la segunda partícula.

La ecuación del movimiento de las partículas son

x=0.975·(t-0.357/0.975)
y=0.357-0.198 ·t

Igualando x=y, se obtiene el instante y la posición del tercer choque

x₂=y₂=0.237

Las velocidades de las partículas antes del segundo choque son:

u_x=0.975, u_y=-0.198

Tercer choque

Las velocidades de las partículas después del choque son:

v_x=-0.328, v_y=0.845

La primera partícula se dirige hacia el extremo izquierdo, la segunda hacia el extremo derecho. Las dos partículas se reflejan en los extremos del carril antes del cuarto choque

La ecuación del movimiento de las partículas son

x=0.328·(t-0.237 /0.328)
y=1.0-0.845(t-0.763/0.845)

Igualando x=y, se obtiene el instante y la posición del cuarto choque

x₃=y₃=0.322

Las velocidades de las partículas antes del segundo choque son:

u_x=0.328, u_y==-0.845

Cuarto choque

Las velocidades de las partículas después del choque son:

v_x=-0.975, v_y=0.197

La primera partícula se dirige hacia el extremo izquierdo, se refleja y choca con la segunda partícula....

Actividades

La longitud del carril se ha fijado en L=1.0 m
La masa de la primera partícula se ha fijado en m_x=1.0
La velocidad inicial de la primera partícula se ha fijado en u_x=1.0
La segunda partícula está inicialmente en reposo, u_y=0.0

Se introduce

La masa de la segunda partícula m_y, actuando en la barra de desplazamiento titulada Masa.
La posición inicial y₀ de la segunda partícula, o del primer choque entre las partículas, actuando en la barra de desplazamiento titulada Posición.

Se pulsa el botón titulado Empieza

Se observa los sucesivos choques y reflexiones de las partículas en los extremos del carril.

En la parte superior del applet se representa

En el eje vertical la posición del choque
En el eje horizontal, el número de choque

Probar los siguientes casos:

Posición del choque y₀=0.5

Masa de la segunda partícula m_y=1.25, 1.5, 1.75, 2.0

Posición del choque y₀=0.2

Masa de la segunda partícula m_y=1.25, 1.5, 1.75, 2.0, 2.25, 2.5

Posición del choque y₀=0.707

Masa de la segunda partícula m_y=1.25, 1.5, 1.75, 2.0

Posición del choque y₀=0.5

Masa de la segunda partícula m_y=0.05, 0.2, 0.35, 0.5

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

De Luca R. Elastic collisions of classical point particles on a finite frictionless linear track with perfectly reflecting endpoints. Eur. J. Phys. 27 (2006) pp. 437-449