• Inicio
• Curso Interactivo de Física

El lenguaje Java y los procedimientos numéricos

Los procedimientos numéricos permiten el tratamiento de problemas que no tienen solución analítica. En el libro “Feynman Lectures on Physics” (Feynman, 1971) se explica el significado de las ecuaciones del movimiento resolviendo numéricamente, las ecuaciones diferenciales correspondientes al movimiento de una masa unida a un muelle elástico y las del movimiento planetario.

Existen potentes programas comerciales como Maple o Mathematica que permiten integrar ecuaciones diferenciales, pero la aproximación que se sigue en el Curso Interactivo es el aprendizaje de la Física, del lenguaje Java y los procedimientos numéricos básicos, a la vez:
El Curso de Lenguaje Java trata de los siguientes temas:

1. Variables. Tipos básicos de datos. El flujo del programa.
2. Clases y objetos. Clases esenciales en Java.
3. La herencia y el polimorfismo
4. Las excepciones.
5. Los applets. El contexto gráfico. Fuentes de texto. Colores.
6. El interfaz de usuario. El modelo de eventos (the AWT Event Model ).
7. Multitarea,  programando una animación.

El objetivo de este Curso es la enseñanza de la Programación Orientada a Objetos y la creación de applets similares a los que se encuentran en el Curso Interactivo de Física, poniendo el énfasis en la parte más difícil de entender, el modelo de eventos.

El Curso de Procedimientos Numéricos trata los siguientes temas:

1. Regresión lineal.
2. Números complejos.
3. Matrices y vectores. Sistema de ecuaciones lineales. Valores propios y vectores propios
4. Búsqueda de raíces. Método del punto medio. Raíces de un polinomio
5. Integración de funciones: método de Simpson.
6. Integración de ecuaciones diferenciales: Método Runge-Kutta.
7. Métodos de Monte Carlo.

Java pertenece a una familia de lenguajes que incluyen al C y C++ en los cuales las rutinas de procedimientos numéricos tienen una sintaxis similar. Se ha tomado de Numerical Recipes (Press, 1992) el código fuente en C de varios métodos que se han traducido al lenguaje Java.

1. Integral elíptica para calcular el periodo de un péndulo para cualquier amplitud

El péndulo simple es uno de los ejemplos más estudiados en un curso de Física, es por otra parte, un ejemplo de oscilador no lineal. Muchos problemas en otras ramas de la Física se pueden reducir a la ecuación diferencial que describe el movimiento de un péndulo. El periodo P de un péndulo para cualquier amplitud es (Puig, 1972).

${\displaystyle P=\frac{2P_0}{\pi }{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\varphi }{\sqrt{1-k^2{\text{sin}}^2\varphi }}}}$

donde P₀ es el periodo para las oscilaciones de pequeña amplitud.
El applet, figura 6, muestra la solución numérica, vemos el pozo de potencial en la parte superior, y la representación del movimiento del péndulo en el espacio de las fases x-v en la parte inferior.

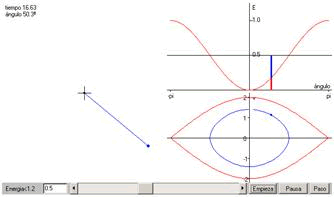
Figura 6. El applet del péndulo simple.

2. Funciones de Bessel en la difracción Fraunhofer de una abertura circular.

Se estudia la difracción Fraunhofer de una abertura circular de radio a. La intensidad en un punto de la pantalla es (Hecht, 1986)

${\displaystyle I(\theta )=I(0){\left(\frac{2J_1(\alpha )}{\alpha }\right)}^2\alpha =\frac{2\pi a}{\lambda }\sin \theta }$

λ es la longitud de onda, θ es la dirección del punto respecto del eje que pasa a través del centro de la abertura, Jn(α) es la función Bessel de orden n.

Los mínimos de intensidad se producen cuando J₁(α)=0, con la excepción de α=0 que es el máximo central. Los máximos secundarios se producen cuando J₂(α)=0, véase la figura 7.

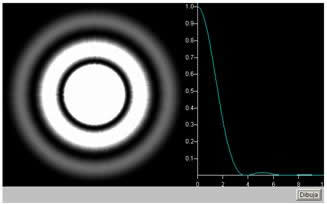
Figura 7.- El applet de la difracción por una abertura circular.

3. Método de Jacobi en el análisis de un sistema de masas acopladas mediante muelles.

Un sistema de masas acopladas es interesante, ya que permite entender el origen de las bandas de energía en la Física del estado sólido.
Se empieza con un sistema de dos masas acopladas mediante muelles. La aplicación del principio de superposición nos lleva a una solución que es la suma de funciones periódicas que oscilan a diferente frecuencia. Después se estudia un sistema de tres masas acopladas. Finalmente, un sistema formado por varias masas acopladas mediante muelles que tienen la misma constante.

En este applet, figura 8, vemos un sistema de 10 masas conectadas mediante muelles de la misma constante k. El applet muestra los modos normales de vibración y proporciona el valor de la frecuencia de cada uno de dichos modos.

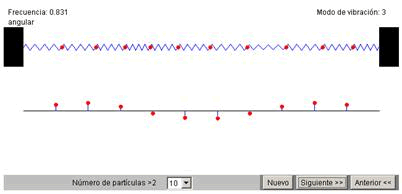
Figura 8.- Modos normales de vibración de una cadena monoatómica.

4. Vibraciones de una cadena que cuelga

En un artículo publicado en la revista American Journal of Physics se plantea un interesante problema: el movimiento hacia arriba y hacia abajo de una cadena (Satterly, 1950). El enunciado del problema es el siguiente: una cadena está apilada en una superficie horizontal, por uno de sus extremos se une a una cuerda inextensible y de masa despreciable, que pasa por una polea, de momento de inercia despreciable. El otro extremo de la cuerda está unido a un peso igual a una longitud a de la cadena, (Davis, 1952). 

La figura 9, muestra la cadena desplaza una distancia x hacia arriba. Las ecuaciones del movimiento son:

${\displaystyle \begin{array}{l}\text{Movimiento hacia arriba}\text{Movimiento hacia abajo}\\ \frac{d^{2}x}{d{t}^2}=\frac{1}{a+x}\left(g(a-x)-{\left(\frac{dx}{dt}\right)}^2\right)\frac{d^{2}x}{d{t}^2}=g\frac{a-x}{a+x}\end{array}}$

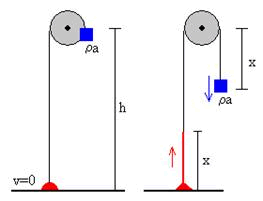
Figura 9.- Posición inicial de la cadena t=0 , y la posición en el instante t.

Para describir el movimiento, tenemos que unir, alternativamente, las soluciones de la primera ecuación diferencial válida para dx/dt>0 con las soluciones de la segunda ecuación diferencial válida para dx/dt<0.
El encuentro se produce en los correspondientes puntos de retorno dx/dt=0, en los instantes en los que x(t) alcanza su máximo o mínimo local, véase la figura 10. Suponiendo las condiciones iniciales x=0, dx/dt=0, la sucesión de los puntos de retorno para el movimiento hacia arriba y para el movimiento hacia abajo de la cadena convergen hacia la posición de equilibrio x/a=1.

La aproximación numérica consiste en escribir el código del procedimiento de Runge_Kutta en una función denominada resolver() de una clase base abstracta RK que llama a una función denominada mover() definida en la clase base e implementada en las clases derivadas MueveArriba y MueveAbajo. La variable rk del tipo RK (clase base abstracta) puede referirse a un objeto de cualquiera de los dos tipos.

La sentencia rk.resolver() está dentro de un bucle y se ejecuta muchas veces. El valor de rk cambia dependiendo si la velocidad dx/dt del extremo de la cadena es positiva o negativa. La función mover que es llamada por el método resolver es la apropiada para el tipo de objeto al cual rk actualmente se refiere. Así, la herencia y el polimorfismo ayudan al programador a mostrar la conducta compleja de este sistema de masa variable.

El applet, figura 10, muestra la solución numérica de este sistema oscilante. El movimiento amortiguado del extremo de la cadena se debe a los procesos disipativos que tienen lugar en el choque de los eslabones de la cadena con el plano horizontal.

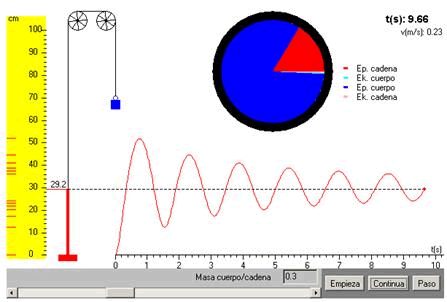
Figura 10.- Vibraciones de una cadena que cuelga.

Curso Interactivo de Física en Internet © Ángel Franco García