Función meromorfa

Una función se denomina meromorfa cuando puede expresarse como razón de dos funciones enteras. Está claro que toda función entera es meromorfa puesto que se puede poner como f(z)/1. Sin embargo, lo recíproco no es cierto, por ejemplo, 1/z es meromorfa pero no entera.

Función periódica

Una función meromorfa f(z) se dice que es periódica si existe un número, distinto de cero tal que

f(z+ω)=f(z)     (1)

para cualquier z (en el caso de que la función tuviera un polo en el punto z, entonces también lo tendría en el punto z+ω).

El número ω que posee tal propiedad (1) se le denomina periodo de la función f(z). Si sustituimos z por z-ω en la expresión (1) obtenemos:

f(z-ω+ω)=f(z-ω)
f(z)=f(z-ω)

para cualquier z. Es decir, si ω es periodo de la función f(z), también lo será -ω. Supongamos ahora que ω₁ y ω₂ son dos periodos (iguales o distintos ) de la función f(z), entonces tendremos:

f(z+ω₁+ω₂)=f(z+ω₁)

esto por ser ω₂ periodo de la función y como ω₁ también lo es, entonces :

f(z+ω₁)=f(z)

de donde deducimos que ω₁+ω₂ también es un periodo de la función f(z).

De la misma manera veríamos que si ω₁, ω₂, ω₃...ω_n son n-periodos de la función f(z), ω₁+ω₂+ω₃...+ω_n es también un periodo de dicha función. En el caso particular en que los n-periodos fuesen iguales tendríamos que nω también es un periodo de la función f(z), y por lo expuesto anteriormente, su opuesto -nω también lo será. De todo ello deducimos la siguiente

Propiedad.- Si ω₁, ω₂, ω₃...ω_n son n-periodos de la función f(z) y p₁,p₂, p₃,..p_n son n-números enteros, entonces p₁ω₁+p₂ω₂+p₃ω₃+...+p_nω_n también es un periodo de f(z).

Teorema

Si f(z) es periódica y no constante, entonces el conjunto de todos los números complejos que son periodos de f(z) no tienen ningún punto de acumulación finito.

Demostración: Supongamos que no se cumple, es decir existe un punto de acumulación ω₀ finito del conjunto de periodos. Entonces por ser ω₀ punto de acumulación tendremos una sucesión de periodos {ω_n}, distintos entre si tal que:

${\displaystyle \underset{n\to \infty }{\lim }\left\{{\omega }_n\right\}={\omega }_0}$

y por tanto: f(ω₁)=f(ω₂)=... =f(ω_p=...

Luego, f(z) toma valores iguales en un conjunto infinito de puntos que tienen como punto de acumulación finito a ω₀, de lo que deducimos que f(z) tiene que ser constante lo cual contradice la hipótesis.

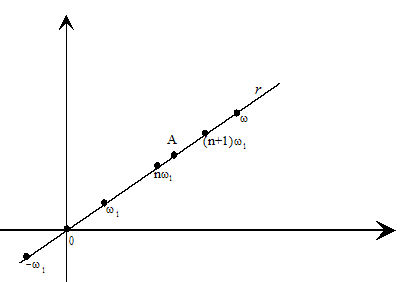
Consecuencia.- Si f(z) no es constante y ω es un periodo distinto de cero de f(z) entonces pω (p=0, ±1, ±2,...) también serán periodos de f(z) y estarán situados en una recta r que pasa por el origen de coordenadas, y por el punto ω. Además, el segmento [-ω, ω] contendrá una cantidad finita de periodos de f(z). Esto nos permitirá poder encontrar un periodo ω₁, distinto de cero (dentro de éste segmento) y que sea el más próximo al origen de coordenadas. Por tanto, en la recta r tendremos un segmento [-ω₁, ω₁], en el cual no existen periodos de f(z) distintos de cero.

Teorema

Cualquier periodo de f(z) situado en esta recta r es de la forma nω₁, donde n es un número entero.

Demostración.- Supongamos que no se cumple, es decir, tenemos un periodo A en la recta r comprendido entre los puntos nω₁ y (n+1)ω₁, entonces,

0<|A-nω₁|<|ω₁|,

con lo cual A-nω₁ es un periodo de f(z) distinto de cero e interior al segmento [-ω₁, ω₁]. Esto está en contradicción con la elección que habíamos hecho del segmento [-ω₁, ω₁].

Función monoperiódica

Una función f(z) decimos que es monoperiódica o simplemente periódica cuando todos los puntos de f(z) se agotan con nω₁.

Periodo fundamental

Llamaremos periodo fundamental al número ω₁ (o también -ω₁) que posee la propiedad de que cualquier periodo de la función se puede expresar como un múltiplo entero del mismo.

Supongamos ahora que f(z) posee periodos que no están situados en la recta r, por ejemplo ω'. Si en el triángulo D' de vértices 0, ω₁, ω' existen periodos distintos de los de los vértices, entonces éstos no pertenecen al segmento [0, ω₁] y como hay una cantidad finita, siempre podremos encontrar un ω₂ cuya distancia a la recta r sea mínima. De aquí se deduce que el triángulo D de vértices 0, ω₁, ω₂ no contiene ningún periodo distinto del de sus vértices y si lo completamos hasta un paralelogramo, tampoco tendrá ningún periodo distinto al de sus vértices, pues si tuviera un ω el ω₁+ω₂-ω también sería periodo y caería en D lo cual no puede ser por su propia construcción (ver figura).

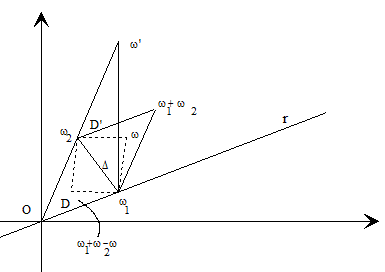
En este caso se puede demostrar que cualquier periodo de la función f(z) se puede expresar por:

m₁ω₁+m₂ω₂     (2)

siendo m₁ y m₂ números enteros

Función elíptica

Una función f(z) decimos que es Elíptica o doblemente Periódica cuando cualquiera de sus periodos se puede expresar mediante (2).

A ω₁ y ω₂ se le denomina periodos fundamentales, y a Δ paralelogramo fundamental.

Teorema

Para una función f(z) doblemente periódica existe un conjunto infinito de pares de periodos fundamentales. Si ω₁ y ω₂ es un par, entonces todos los demás están dados por:

Ω₁=l₁ω₁+l₂ω₂     Ω₂=k₁ω₁+k₂ω₂

donde

${\displaystyle \left|\begin{array}{cc}{l}_1& l_2\\ k_1& k_2\end{array}\right|=\pm 1}$

con l₁, l₂, k₁, k₁ enteros.

Demostración.- Ω₁=l₁ω₁+l₂ω₂, Ω₂=k₁ω₁+k₂ω₂

Operando

${\displaystyle {\omega }_1=\frac{k_2{\Omega }_1}{A}-\frac{l_2{\Omega }_2}{A}{\omega }_2=\frac{l_1{\Omega }_2}{A}-\frac{k_1{\Omega }_1}{A}}$

donde

${\displaystyle A=\left|\begin{array}{cc}{l}_1& l_2\\ k_1& k_2\end{array}\right|}$

y como A=±1 tenemos que ω₁ y ω₂ se pueden expresar como una combinación de Ω₁ y Ω₂ donde los coeficientes son enteros.

Entonces para cualquier periodo ω de la función

${\displaystyle \omega =p_1{\omega }_1+p_2{\omega }_2=p_1\left(\frac{k_2{\Omega }_1-l_2{\Omega }_2}{A}\right)+p_2\left(\frac{l_1{\Omega }_2-k_1{\Omega }_1}{A}\right)}$

es decir,

${\displaystyle \omega =\mu {\Omega }_1+\delta {\Omega }_2,\mu ,\delta \in Z}$

donde deducimos que Ω₁ y Ω₂ es un par fundamental. Además como existe un conjunto infinito de cuaternas de números enteros que cumplen la condición (2), tendremos un conjunto infinito de pares fundamentales distintos, y asociados a estos, un conjunto infinito de paralelogramos fundamentales.

Teorema

Las áreas de todos los paralelogramos fundamentales son iguales para una función f(z) doblemente periódica.

Demostración.- Sean ω₁=a₁+i·b₁ y ω₂=a₂+i·b₂ un par fundamental y Ω₁, Ω₂ otro par fundamental, entonces por el teorema anterior

Ω₁=λ₁(a₁+i·b₁)+λ₂(a₂+i·b₂)
Ω₂=k₁(a₁+i·b₁)+k₂(a₂+i·b₂)

Donde el valor del determinante

${\displaystyle \left|\begin{array}{cc}{\lambda }_1& {\lambda }_2\\ k_1& k_2\end{array}\right|=\pm 1}$

Ahora

${\displaystyle \begin{array}{l}\text{Área}\text{(paralelogramo}{\Omega }_1,{\Omega }_2)=\left|\begin{array}{cc}{\lambda }_1{a}_1+{\lambda }_2{a}_2& {\lambda }_1{b}_1+{\lambda }_2{b}_2\\ k_1{a}_1+k_2{a}_2& k_1{b}_1+k_2{b}_2\end{array}\right|=\\ =\pm \left|\begin{array}{cc}{\lambda }_1& {\lambda }_2\\ k_1& k_2\end{array}\right|.\left|\begin{array}{cc}{a}_1& b_1\\ a_2& b_2\end{array}\right|=\pm \left|\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right|=\pm \text{Área}\text{(paralelogramo}{\omega }_1,{\omega }_2)\end{array}}$

Teorema de Jacobi

Una función periódica no constante f(z) es simple o doblemente periódica.