Definición

A la función que figura entre las llaves se le representa por ℘(z) y se le denomina función p de Weierstrass (se lee pe de z y al signo ℘ se le llama signo de Weierstrass)

${\displaystyle \wp (z)=\frac{1}{z^2}+{\displaystyle \sum _{\Omega \ne 0}\left[\frac{1}{{(z-\Omega )}^2}-\frac{1}{{\Omega }^2}\right]}.}$

Propiedades de ℘(z)

1. La función ℘(z) es meromorfa con polos de segundo orden en cada uno de los puntos Ω (incluyendo el origen de coordenadas). Y una parte principal

${\displaystyle \frac{1}{{(z-\Omega )}^2}}$

2. La serie que define a ℘(z) es absolutamente convergente.

Para demostrarlo vamos a considerar solamente los términos de la serie que cumplen que |Ω|>2|z|, entonces

${\displaystyle \begin{array}{l}\left|\frac{1}{{(z-\Omega )}^2}-\frac{1}{{\Omega }^2}\right|=\left|\frac{{\Omega }^2-z^2-{\Omega }^2+2\Omega z}{{\Omega }^2{(z-\Omega )}^2}\right|=\left|\frac{z(2\Omega -z)}{{\Omega }^2{(z-\Omega )}^2}\right|\le \\ \le \frac{2\left|\Omega \right|\left(1+\frac{\left|z\right|}{2\left|\Omega \right|}\right)\left|z\right|}{{\left|\Omega \right|}^4{\left(1-\frac{\left|z\right|}{\left|\Omega \right|}\right)}^2}=\frac{2\left(1+\frac{\left|z\right|}{2\left|\Omega \right|}\right)\left|z\right|}{{\left|\Omega \right|}^3{\left(1-\frac{\left|z\right|}{\left|\Omega \right|}\right)}^2}<\end{array}}$

y como {|z|/|Ω|}<1/2 tenemos

${\displaystyle <\frac{2\left(1+\frac{1}{4}\right)\left|z\right|}{{\left|\Omega \right|}^3\frac{1}{4}}=\frac{10\left|z\right|}{{\left|\Omega \right|}^3}}$

y como la serie ${\displaystyle \sum \frac{1}{{\left|\Omega \right|}^{\lambda }}}$ era convergente para λ>2 se deduce que la serie nuestra converge absolutamente como queríamos demostrar.

3. La función ℘(z) es una función par.

Para ello calculemos ℘(-z)

${\displaystyle \begin{array}{l}\wp (-z)=\frac{1}{{(-z)}^2}+{\displaystyle \sum _{\Omega \ne 0}\left[\frac{1}{{(-z-\Omega )}^2}-\frac{1}{{\Omega }^2}\right]}=\frac{1}{z^2}+{\displaystyle \sum _{\Omega \ne 0}\left[\frac{1}{{(z+\Omega )}^2}-\frac{1}{{\Omega }^2}\right]}=\\ =\frac{1}{z^2}+{\displaystyle \sum _{\Omega \ne 0}\left[\frac{1}{{\left[z-(-\Omega )\right]}^2}-\frac{1}{{(-\Omega )}^2}\right]}\end{array}}$

Esta última serie se diferencia de la serie

${\displaystyle \frac{1}{z^2}+{\displaystyle \sum _{\Omega \ne 0}\left[\frac{1}{{(z-\Omega )}^2}-\frac{1}{{\Omega }^2}\right]}}$

sólo en el orden de sus términos, por lo tanto la suma es la misma, es decir

${\displaystyle \wp (z)=\wp (-z).}$

4. La función ℘(z) es doblemente periódica y sus periodos fundamentales son 2ω₁ y 2ω₃

Para demostrar esto , vamos a calcular la derivada de ℘(z)

${\displaystyle \wp \text{'}(z)=-\frac{2}{z^3}-{\displaystyle \sum _{\Omega \ne 0}\frac{2}{{(z-\Omega )}^3}=-2\left[\frac{1}{z^3}+{\displaystyle \sum _{\Omega \ne 0}\frac{1}{{(z-\Omega )}^3}}\right]}=-2g(z)}$

pues

${\displaystyle g(z)={\displaystyle \sum \frac{1}{{(z-\Omega )}^3}}}$

y como sólo se diferencian en un factor numérico, tenemos que la función ℘'(z) es doblemente periódica de periodos 2ω₁ y 2ω₃ igual que la función g(z).
Por lo tanto,

${\displaystyle \wp \text{'}(z+2{\omega }_j)=\wp \text{'}(z)}$ para j=1, 3

e integrando

${\displaystyle \wp (z+2{\omega }_j)=\wp (z)+C_j}$ para j=1, 3

Haciendo z=-ω_j, obtenemos:

${\displaystyle \wp ({\omega }_j)=\wp (-{\omega }_j)+C_j}$ para j=1, 3

pero por la propiedad anterior la función ℘(z) es par, luego,

C_j=0 para j=1, 3 y por tanto, $\wp (z+2{\omega }_j)=\wp (z)$

La función ℘(z) es doblemente periódica como queríamos demostrar.

Del mismo modo que en el caso de la función g(z) vamos a comprobar que dichos periodos son fundamentales.

Sea ω un periodo cualquiera de la función ℘(z). Como Ω es un polo de ℘(z), ω+Ω tiene que ser uno de los polos, es decir,

ω+Ω=Ω₁ de donde $\omega ={\Omega }_1-\Omega =m_{1}2{\omega }_1+m_{2}2{\omega }_3,m_1,m_2\in Z$

5. La función ℘(z) es elíptica de orden dos.

Al paralelogramo fundamental de periodos de la función ℘(z) con los vértices 0, 2ω₁, 2ω₂, 2ω₃ se le debe adjuntar solamente un polo doble en el origen de coordenadas, los otros tres pertenecen a los paralelogramos vecinos.

Conclusión ℘(z) es una función elíptica de segundo orden. Las partes principales correspondientes a sus polos son de la forma

${\displaystyle \frac{1}{{(z-\Omega )}^2}}$

Propiedades de su función derivada ℘'(z)

${\displaystyle \wp \text{'}(z)=-2{\displaystyle \sum \frac{1}{{(z-\Omega )}^3}}}$

1. Es una función meromorfa con polos de tercer orden en cada uno de los puntos Ω (incluyendo el origen de coordenadas) y una parte principal

${\displaystyle \frac{1}{{(z-\Omega )}^3}}$

2. La función ℘'(z) es doblemente periódica cuyos periodos fundamentales son 2ω₁ y 2ω₃.

Sólo se diferencia en un factor numérico de la función elíptica g(z) de periodos fundamentales 2ω₁ y 2ω₃ considerada anteriormente.

3. ℘'(z) es una función elíptica de orden tres, (ya visto con la función g(z))

4. La función ℘'(z) es impar al igual que la función g(z)

5. Los puntos ω₁, ω₃, ω₁+ω₃=ω₂ y todos sus puntos congruentes son ceros de la función ℘'(z).

Ya lo teníamos demostrado con la función g(z), pero ahora lo vamos a demostrar de otra manera. Como la función ℘'(z) es elíptica de orden tres por uno de los teoremas vistos anteriormente, tendrá tres A-puntos en el paralelogramo fundamental de periodos y podemos distinguir los siguientes casos:

1. Si A=∞, estos tres puntos se convierten en un punto triple (el origen de coordenadas si se trata del paralelogramo fundamental de periodos)

2. Si A≠∞, caso particular A=0, obtenemos los tres ceros .Veamos,

${\displaystyle \wp \text{'}(-z+2{\omega }_j)=\wp \text{'}(-z)=-\wp \text{'}(z)}$ para j=1, 2, 3 y haciendo z=ω_j tenemos

${\displaystyle \wp \text{'}({\omega }_j)=-\wp \text{'}({\omega }_j)\text{y}\text{como}\wp \text{'}({\omega }_j)\ne \infty }$

${\displaystyle 2\wp \text{'}({\omega }_j)=0\Rightarrow \wp \text{'}({\omega }_j)=0j=\mathrm{1,2,3}}$



Estos ceros serán simples pues en caso contrario la cantidad de ceros en el paralelogramo fundamental sería mayor que tres.

Con todo lo visto podemos enunciar para la función ℘(z) la siguiente:

Propiedad.- Los A-puntos de la función ℘(z) para todos los posibles valores complejos de A, están situados simétricamente respecto del centro del paralelogramo (en el interior de él) o respecto de los puntos medios de sus lados (en los lados). Además, los puntos que están situados en el centro o en los puntos medios de los lados así como el situado en el ángulo inferior de la izquierda del paralelogramo son dobles. (Este último polo doble).

Demostración.- Para cualquier valor de A ,existen dos A-puntos en el paralelogramo de periodos, pues la función ℘(z) es de orden dos.

1. Caso de A=∞ los dos puntos se convierten en un polo doble (en el origen de coordenadas, si se trata del paralelogramo fundamental de periodos)

2. A≠∞ aquí a su vez vamos a distinguir:

1. Si A tiene uno de los valores

${\displaystyle \wp ({\omega }_j)=e_j\text{para}(j=\mathrm{1,2,3})}$

los A-puntos correspondientes se confunden dos a dos en los puntos ω₁, ω₂, ω₃, pues,

${\displaystyle \wp \text{'}({\omega }_j)=0y\wp \text{'}\text{'}({\omega }_j)\ne 0\text{para}j=\mathrm{1,2,3}}$

es decir los puntos ω₁, ω₂, ω₃ son dobles para la función ℘(z).

2. A≠e_j, j= 1, 2, 3 tenemos pares de A-puntos distintos entre sí, pues en caso contrario ℘'(z) tendría ceros en el paralelogramo de periodos, además de los tres puntos ω₁, ω₂, ω₃, lo que es imposible pues es de orden tres.

Vamos a ver la posición de cada par en el paralelogramo.

${\displaystyle \wp (-z+2{\omega }_j)=\wp (-z)=\wp (z)\text{por}\text{ser}\wp (z)\text{par}(j=\mathrm{1,2,3})}$

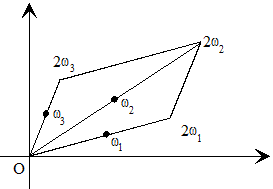
Luego ℘(z) toma valores iguales en los puntos z y 2ω_j-z y estos puntos cumplen

${\displaystyle \frac{z+(2{\omega }_j-z)}{2}={\omega }_j(j=\mathrm{1,2,3})}$

es decir, son simétricos respecto de ω_j. Véase la figura, caso j=1.



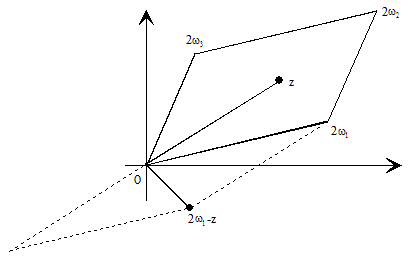
Sea A≠∞ y A≠e_j, si z₁ es uno de los A-puntos de la función ℘(z), entonces

z₁≠0 y z₁≠ω_j (j=1, 2, 3)

Si z₁ está situado en el interior del paralelogramo fundamental de periodos, 2ω₂-z₁ también está situado en el interior del mismo, simétricamente respecto del centro ω₂ del paralelogramo y por tanto es el segundo A-punto de la función ℘(z).



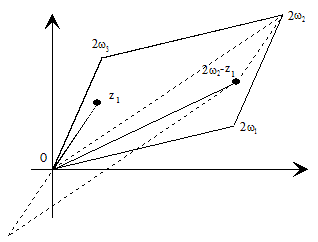
Si z₁ está situado en el lado que une los vértices 0 y 2ω_j (j=1, 3) del paralelogramo fundamental, entonces 2ω_j-z₁ está situado en el mismo lado y simétricamente respecto del punto medio ω_j de este lado, y por tanto, es el segundo A-punto de la función ℘(z).

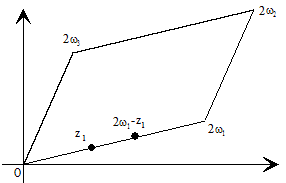
Estudio de la función ℘(z) en dos casos particulares

Primer caso

Supongamos que 2ω₁ es un número real positivo 2α y 2ω₃ un número imaginario puro 2β·i con (β>0). Aquí los paralelogramos de periodos son rectángulos.

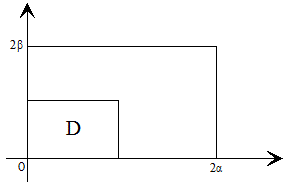
Vamos a estudiar la función ℘(z) en el rectángulo D de la figura

${\displaystyle D:0\le x\le \alpha ,0\le y\le \beta .}$

Por lo visto anteriormente, no pueden pertenecer a este rectángulo dos A-puntos distintos de la función ℘(z), exceptuando los puntos dobles que están situados en los vértices del rectángulo, luego ℘(z) toma valores distintos en diferentes puntos del rectángulo

${\displaystyle \wp (z_1)\ne \wp (z_2)\text{si}{z}_1\ne z_2,z_1,z_2\in D}$

y como es uniforme y analítica en este recinto a excepción de polos, es univalente. Por tanto, ℘(z) nos transforma D biunívoca y conformemente en otro recinto G del plano z.
Entonces nos queda estudiar la imagen de la frontera del rectángulo D.

Véamos

${\displaystyle \begin{array}{l}\wp (x+iy)=\frac{1}{{(x+iy)}^2}+{\displaystyle \sum _{\Omega \ne 0}\left[\frac{1}{{(x+iy-2m\alpha -2ni\beta )}^2}-\frac{1}{{(2m\alpha +2ni\beta )}^2}\right]},\\ \\ \text{Siendo }\Omega \text{=}2m\alpha +2ni\beta \end{array}}$

Calculemos ahora su conjugado

${\displaystyle \overline{\wp (x+iy)}=\frac{1}{{(x-iy)}^2}+{\displaystyle \sum _{\Omega \ne 0}\left[\frac{1}{{(x-iy-2m\alpha +2ni\beta )}^2}-\frac{1}{{(2m\alpha -2ni\beta )}^2}\right]}}$

y comparémoslo con

${\displaystyle \wp (x-iy)=\frac{1}{{(x-iy)}^2}+{\displaystyle \sum _{\Omega \ne 0}\left[\frac{1}{{(x-iy-2m\alpha -2ni\beta )}^2}-\frac{1}{{(2m\alpha +2ni\beta )}^2}\right]},}$

Pero el conjunto de números 2mα-2niβ para todas las combinaciones posibles de los números enteros m y n es el mismo que el de los números 2mα+2niβ (los periodos de la función ℘(z)). Es decir, las series sólo se diferenciarán en el orden de sus términos, luego

${\displaystyle \overline{\wp (x+iy)}=\wp (x-iy).}$

1. En el caso particular de y=0

${\displaystyle \overline{\wp (x)}=\wp (x)}$

Con lo cual tenemos que la función ℘(z) es un número real para cualquier x real.

2. Si z=α+i·y tenemos por una parte

${\displaystyle \overline{\wp (\alpha +iy)}=\wp (\alpha -iy).}$

y por otra, como α+i·y y α-i·y son simétricos respecto de ω₁=α

${\displaystyle \wp (\alpha +iy)=\wp (\alpha -iy).}$

También llegamos a la conclusión de que los valores de ℘(α+i·y) son reales para cualquier valor de y

3. Si z₁=x+i·β, z₂=x-i·β tenemos que z₁=z₂+2i·β y como 2i·β es el periodo de la función ℘(z)

${\displaystyle \wp (x+i\beta )=\wp (x-i\beta )}$

luego también son reales para cualquier x.

4. Por último, como la función ℘(z) es par,

${\displaystyle \wp (iy)=\wp (-iy).}$

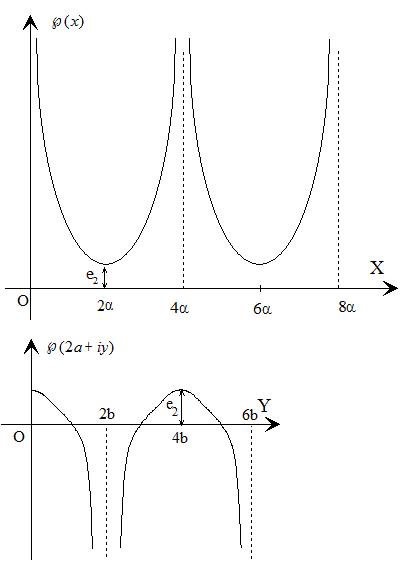
Conclusión.- La función ℘(z) toma valores reales en los lados del rectángulo de periodos y en las líneas medias (luego en los lados del rectángulo D)

PROPIEDAD.- La función ω=℘(z) de periodos fundamentales 2α y 2β·i, transforma conformemente el rectángulo 0<x<α y 0<x<β en el semiplano inferior

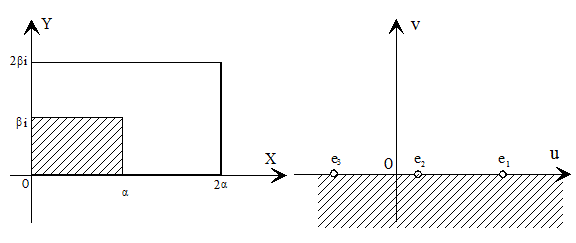
Si el punto z describe el contorno del rectángulo D en sentido contrario al del movimiento de las agujas del reloj, comenzando en el vértice z=0, entonces el punto ω=℘(z) se mueve sobre el eje real, comenzando desde ℘(0)=∞ y terminando en el mismo punto, y lo hace todo el tiempo hacia un mismo lado, es decir, no pasa dos veces sobre el mismo punto. Luego variando continuamente desde -∞ hasta ∞ el punto ω=℘(z) describe una sola vez el eje real.

Para los valores reales z=x próximos a cero, en la expresión de ℘(z) predomina el término 1/x² de donde, deducimos que el punto ω parte de +∞ y se mueve por el eje real pasando por los puntos intermedios

${\displaystyle \begin{array}{l}\wp ({\omega }_1)=\wp (\alpha )=e_1,\wp ({\omega }_2)=\wp (\alpha +\beta i)=e_2,\wp ({\omega }_3)=\wp (\beta i)=e_3\\ e_1>e_2>e_3\end{array}}$

(en este orden) dirigiéndose hacia -∞, pues cuando z=i·y e y está próximo a cero en ℘(i·y) predomina el término -1/y²

Como el contorno del rectángulo D se transforma en el eje real, este rectángulo se transforma en un semiplano, además al recorrer el contorno en sentido contrario al movimiento de las agujas del reloj, el rectángulo D queda a la izquierda del observador, por lo tanto, el semiplano correspondiente tiene que quedar a la izquierda del observador cuando se recorre el eje real en dirección de decrecimiento, es decir, será el semiplano inferior como queríamos demostrar.

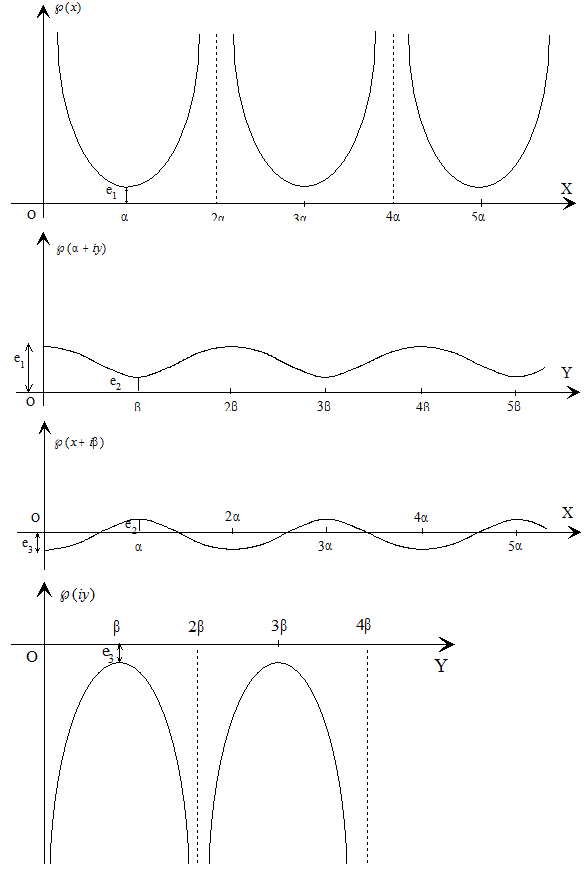
Además, como la función ℘(z) toma valores iguales en los puntos que son simétricos respecto de los semiperiodos ω₁, ω₃ llegamos a la conclusión de que dicha función tomará dos veces todos los valores reales del intervalo (e₁, +∞) en el lado del paralelogramo fundamental

${\displaystyle 0\le x\le 2\alpha ,y=0}$

dos veces los valores del intervalo (e₂, e₁) en la línea media,

${\displaystyle x=\alpha ,0\le y\le 2\beta ,}$

dos veces los valores del intervalo (e₃, e₂) en la línea media,

${\displaystyle 0\le x\le 2\alpha ,y=\beta }$

y finalmente, dos veces los valores reales del intervalo (-∞, e₃) en el lado

${\displaystyle x=0,0\le y\le 2\beta }$

En todos los demás puntos del paralelogramo fundamental, como ℘(z) es una función de segundo orden, tomará valores imaginarios.

Segundo caso

Supongamos ahora que los periodos son conjugados.

${\displaystyle 2{\omega }_1=2a-2bi,2{\omega }_3=2a+2bi}$

Entonces los paralelogramos de periodos son rombos cuyas diagonales son paralelas al eje real e imaginario, respectivamente.

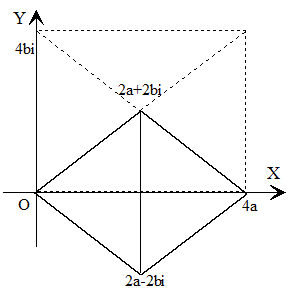
Como,

${\displaystyle 2{\omega }_3+2{\omega }_1=4a,2{\omega }_3-2{\omega }_1=4bi}$

la función ℘(z) posee un periodo real 4a y otro imaginario puro 4b·i, pero la diferencia con el caso anterior es que estos periodos no son fundamentales, porque el rectángulo construido sobre los lados 4a y 4b·i contienen en su interior (en el centro) un periodo el 2a+2b·i.
En este caso,

${\displaystyle \begin{array}{l}\wp (x+iy)=\frac{1}{{(x+iy)}^2}+{\displaystyle \sum _{\Omega \ne 0}\left\{\frac{1}{{\left[x+iy-2(a-bi)m-2(a+bi)n\right]}^2}-\frac{1}{{\left[2(a-bi)m+2(a+bi)n\right]}^2}\right\}}\\ \\ \text{siendo}\Omega =2(a-bi)m+2(a+bi)n\\ \\ \overline{\wp (x+iy)}=\frac{1}{{(x-iy)}^2}+{\displaystyle \sum _{\Omega \ne 0}\left\{\frac{1}{{\left[x-iy-2(a+bi)m-2(a-bi)n\right]}^2}-\frac{1}{{\left[2(a+bi)m+2(a-bi)n\right]}^2}\right\}}\\ \wp (x-iy)=\frac{1}{{(x-iy)}^2}+{\displaystyle \sum _{\Omega \ne 0}\left\{\frac{1}{{\left[x-iy-2(a-bi)m-2(a+bi)n\right]}^2}-\frac{1}{{\left[2(a-bi)m+2(a+bi)n\right]}^2}\right\}}\end{array}}$

Como los números 2(a+b·i)m+2(a-b·i)n para todas las combinaciones posibles de los enteros m y n forman el mismo conjunto de números (los periodos de la función ℘(z)) que los números 2(a-b·i)m+2(a+b·i)n. Entonces, los términos de estas dos últimas series sólo se diferenciarán en el orden, luego,

${\displaystyle \overline{\wp (x+iy)}=\wp (x-iy)}$

En particular tomando y=0

${\displaystyle \overline{\wp (x)}=\wp (x)}$

Como vemos la función ℘(z) es real para cualquier x.

Por otra parte, los puntos 2a+i·y y 2a-i·y son simétricos respecto del semiperiodo ω₂=2a por consiguiente,

${\displaystyle \wp (2a+iy)=\wp (2a-iy)}$

y por lo visto anteriormente

${\displaystyle \overline{\wp (2a+iy)}=\wp (2a-iy)}$

luego

${\displaystyle \overline{\wp (2a+iy)}=\wp (2a+iy)}$

Llegamos a la conclusión de que ℘(2a+i·y) también toma valores reales para cualquier valor de y. Esto significa que la función ℘(z) toma valores reales en cada una de las diagonales del rombo.
En el segmento 0≤x≤2a, y=0 decrece de +∞ hasta ℘(ω₂)=℘(2a)=e₂ y después en el segmento x=2a, 0≤y≤2b continúa decreciendo desde e₂ hasta -∞.
Luego deducimos que ℘(z) toma dos veces cada valor real mayor que e₂ en la diagonal del paralelogramo fundamental situada en el eje real, y toma también dos veces cada valor real menor que e₂ en la diagonal que es perpendicular al eje real.
En los puntos del paralelogramo fundamental que no están situados en la diagonal, la función toma valores imaginarios. En particular

${\displaystyle e_1=\wp ({\omega }_1)=\wp (a-bi),e_3=\wp ({\omega }_3)=\wp (a+bi)}$

Como la función ℘(z) es periódica, en el eje imaginario también toma valores reales

${\displaystyle \wp (iy)=\wp \left[2a+i(y+2b)\right]}$

Desarrollo en serie de Laurent de la función ℘(z)

Sea

${\displaystyle \begin{array}{l}A(z)=\frac{1}{{(z-\Omega )}^2}-\frac{1}{{\Omega }^2}=\frac{1}{{\Omega }^2}\left[{\left(1-\frac{z}{\Omega }\right)}^{-2}-1\right]\Omega \ne 0\\ A\text{'}(z)=\frac{-2}{{\Omega }^2}{\left(1-\frac{z}{\Omega }\right)}^{-3}\left(\frac{-1}{\Omega }\right)=\frac{2}{{\Omega }^3}{\left(1-\frac{z}{\Omega }\right)}^{-3},A\text{'}(0)=\frac{2}{{\Omega }^3}\\ A\text{'}\text{'}(z)=\frac{2(-3)}{{\Omega }^3}{\left(1-\frac{z}{\Omega }\right)}^{-4}\left(\frac{-1}{\Omega }\right)=\frac{2.3}{{\Omega }^4}{\left(1-\frac{z}{\Omega }\right)}^{-4},A\text{'}\text{'}(0)=\frac{2.3}{{\Omega }^4}\\ .\\ .\\ .\\ A^{(n}(z)=\frac{\mathrm{2.3...}n(n+1)}{{\Omega }^{n+2}}{\left(1-\frac{z}{\Omega }\right)}^{-(n+2)},A^{(n}(0)=\frac{\mathrm{2.3...}n(n+1)}{{\Omega }^{n+2}}.\\ \text{Luego}\\ \text{A(z)=}{\displaystyle \sum _1^{\infty }\frac{n+1}{{\Omega }^{n+2}}{z}^n}\end{array}}$

Aplicando el criterio de D'Alembert

${\displaystyle \begin{array}{l}\left|\frac{u_{n+1}}{u_n}\right|=\left|\frac{(n+2)z^{n+1}}{{\Omega }^{n+3}}:\frac{(n+1)z^n}{{\Omega }^{n+2}}\right|=\left|\frac{(n+2)z}{(n+1)\Omega }\right|=\frac{(n+2)}{(n+1)}\left|\frac{z}{\Omega }\right|\\ \underset{n\to \infty }{\lim }\frac{(n+2)}{(n+1)}\left|\frac{z}{\Omega }\right|=\left|\frac{z}{\Omega }\right|<1\Rightarrow \left|z\right|<\left|\Omega \right|\end{array}}$

La serie es convergente en el círculo |z|<|Ω|.

De todo esto tenemos para ℘(z) el siguiente desarrollo en serie de potencias de z

${\displaystyle \begin{array}{l}\wp (z)=\frac{1}{z^2}+{\displaystyle \sum _{\Omega \ne 0}\left[\frac{2z}{{\Omega }^3}+\frac{3z^2}{{\Omega }^4}+\frac{4z^3}{{\Omega }^5}+\mathrm{...}+\frac{(n+1)z^n}{{\Omega }^{n+2}}+\mathrm{...}\right]}=\\ =\frac{1}{z^2}+2{\displaystyle \sum _{\Omega \ne 0}\frac{1}{{\Omega }^3}}z+3{\displaystyle \sum _{\Omega \ne 0}\frac{1}{{\Omega }^4}}{z}^2+\mathrm{...}+(n+1){\displaystyle \sum _{\Omega \ne 0}\frac{1}{{\Omega }^{n+2}}}{z}^n+\mathrm{...}\end{array}}$

el cual es convergente en el recinto 0<|z|<ζ (siendo ζ el menor de los módulos de los periodos distintos de cero).
Ahora bien, la función ℘(z) es par, por lo tanto todos los coeficientes de las potencias impares de z valen cero. Así,

${\displaystyle \wp (z)=\frac{1}{z^2}+c_2{z}^2+c_4{z}^4+\mathrm{...}+c_{2m}{z}^{2m}+\mathrm{...}}$

donde

${\displaystyle c_{2m}=(2m+1){\displaystyle \sum _{\Omega \ne 0}\frac{1}{{\Omega }^{2m+2}}}}$

Derivando obtenemos

${\displaystyle \wp \text{'}(z)=\frac{-2}{z^3}+2c_{2}z+4c_4{z}^3+\mathrm{...}+2m{c}_{2m}{z}^{2m-1}+\mathrm{...}}$

Relación algebraica entre las funciones ℘(z) y ℘'(z)

Formamos una combinación sencilla de las funciones ℘(z) y ℘'(z) que no tenga polos en el paralelogramo fundamental. Dicha combinación tendrá que ser una función elíptica (por serlo ℘(z) y ℘'(z)) sin polos, por lo tanto constante.

Viendo que las partes principales de los desarrollos de ℘(z) y ℘'(z) son 1/z² y -2/z³ respectivamente, podemos poner la combinación

${\displaystyle \begin{array}{l}{\left[\wp \text{'}(z)\right]}^2=-4{\left[\wp (z)\right]}^3\\ {\left[\wp \text{'}(z)\right]}^2=\left[\frac{4}{z^6}-\frac{8c_2}{z^2}-16c_4+\mathrm{...}\right];{\left[\wp (z)\right]}^3=\left[\frac{1}{z^6}+\frac{3c_2}{z^2}+3c_4+\mathrm{...}\right]\end{array}}$

entonces,

${\displaystyle {\left[\wp \text{'}(z)\right]}^2-4{\left[\wp (z)\right]}^3=-\frac{20c_2}{z^2}-28c_4-\mathrm{...}}$

Los términos que no se han puesto contienen potencias no negativas de z.
Si añadimos a la expresión obtenida el término 20c₂℘(z) tenemos,

${\displaystyle {\left[\wp \text{'}(z)\right]}^2-4{\left[\wp (z)\right]}^3+20c_2\wp (z)=-28c_4-\mathrm{...}}$

Luego, la combinación buscada.

El primer miembro, representa una función elíptica (pues sus sumandos lo son) que no tiene polos en el paralelogramo fundamental de periodos, luego por lo tanto será una constante.

En el segundo miembro, para z=0 el valor que se obtiene es -28c₄ por lo cual

${\displaystyle \begin{array}{l}{\left[\wp \text{'}(z)\right]}^2-4{\left[\wp (z)\right]}^3+20c_2\wp (z)=-28c_4\\ {\left[\wp \text{'}(z)\right]}^2=4{\left[\wp (z)\right]}^3-20c_2\wp (z)-28c_4\end{array}}$

Ecuación diferencial de primer orden que satisface la función ℘(z).

Los coeficientes 20c₂ y 28c₄ los designaremos por:

${\displaystyle \begin{array}{l}{g}_2=20c_2=\mathrm{3.4.5}{\displaystyle \sum _{\Omega \ne 0}\frac{1}{{\Omega }^4}}\\ g_3=28c_4=\mathrm{4.5.7}{\displaystyle \sum _{\Omega \ne 0}\frac{1}{{\Omega }^6}}\\ \text{pues}\text{,}{\text{c}}_2=3{\displaystyle \sum _{\Omega \ne 0}\frac{1}{{\Omega }^4}}y{\text{c}}_4=5{\displaystyle \sum _{\Omega \ne 0}\frac{1}{{\Omega }^6}}\end{array}}$

Y los denominaremos INVARIANTES de la función ℘(z).

Esta denominación se debe a que no dependen de la forma en que se hayan elegido los periodos fundamentales de la función ℘(z).

Además, como sabíamos que la serie

${\displaystyle {\displaystyle \sum _{\Omega \ne 0}\frac{1}{{\left|\Omega \right|}^{\lambda }}}\text{es}\text{convergente}\forall \lambda \text{>2}}$

tenemos que los invariantes son sumas de series absolutamente convergentes,extendidas al conjunto de todos los periodos de la función ℘(z) que son distintos de cero.

Resumiendo, la ecuación obtenida es:

${\displaystyle {\left[\wp \text{'}(z)\right]}^2=4{\left[\wp (z)\right]}^3-g_2\wp (z)-g_3}$

y si hacemos ℘(z)=v tenemos

${\displaystyle {\left[\frac{dv}{dz}\right]}^2=4v^3-g_{2}v-g_3.}$

Pero la función ℘'(z) tiene los ceros ω₁, ω₂, ω₃ luego, el polinomio 4v³-g₂v-g₃ se anulará en

${\displaystyle v_j=\wp ({\omega }_j)=e_j,j=\mathrm{1,2,3}}$

y podremos poner

${\displaystyle 4v^3-g_{2}v-g_3=4(v-e_1)(v-e_2)(v-e_3)}$

con lo cual la ecuación nos quedará

${\displaystyle {\left[\wp \text{'}(z)\right]}^2=4\left[\wp (z)-e_1\right]\left[\wp (z)-e_2\right]\left[\wp (z)-e_3\right]}$

Además como los números e₁, e₂, e₃ son distintos entre sí, el discriminante de la ecuación

${\displaystyle 4v^3-g_{2}v-g_3=0}$

tiene que ser distinto de cero

${\displaystyle \Delta =\frac{1}{16}(g_2{}^3-27g_3{}^2)={(e_2-e_3)}^2{(e_3-e_1)}^2{(e_1-e_2)}^2\ne \mathrm{0,}}$

y de las relaciones anteriores se obtienen:

${\displaystyle \begin{array}{l}{e}_1+e_2+e_3=0\\ e_1{e}_2+e_2{e}_3+e_3{e}_1=-\frac{g_2}{4}\\ e_1.e_2.e_3=\frac{g_3}{4}\end{array}}$

La relación

${\displaystyle {\left[\wp \text{'}(z)\right]}^2-4{\left[\wp (z)\right]}^3+20c_2\wp (z)+28c_4=0}$

tiene una interpretación importante: consideremos la curva algebraica

${\displaystyle y^2=4x^3-20c_{2}x-28c_4}$

las fórmulas x=℘(z), y=℘'(z) dan una representación paramétrica de esta curva.
Se puede demostrar que para todo punto (x, y)∈C×C de la curva algebraica, existe un z∈C y sólo uno tal que

${\displaystyle x=\wp (z),y=\wp \text{'}(z)}$

Por otra parte en

${\displaystyle {\left[\frac{dv}{dz}\right]}^2=4v^3-g_{2}v-g_3}$

para cada valor de v nos da dos valores de v' que sólo se diferencian en el signo. Esto concuerda con el hecho de que la función ℘(z) es par y la función ℘'(z) es impar. Pero como la función ℘(z) es uniforme, de la expresión

${\displaystyle \wp \text{'}(z)=\sqrt{4{\left[\wp (z)\right]}^3-g_2\wp (z)-g_3}}$

entre los dos valores de la raíz tendremos que elegir cada vez el que da el valor ℘'(z).

Obtención de la integral elíptica de primera especie en la forma normal de Weierstrass

Vamos a considerar una curva rectificable γ que una el punto z₀ con otro punto z y que no pase por los polos de la función ℘(z).
Poniendo

${\displaystyle dz=\frac{d\wp (z)}{\sqrt{4{\left[\wp (z)\right]}^3-g_2\wp (z)-g_3}}}$

e integrando a lo largo de la curva γ, obtenemos

${\displaystyle z-z_0={\displaystyle \underset{\gamma }{\int }\frac{d\wp (z)}{\sqrt{4{\left[\wp (z)\right]}^3-g_2\wp (z)-g_3}}.}}$

Por otra parte, si la imagen de la curva γ en el plano w es la curva ℘(z)=Γ que une los puntos w₀=℘(z₀) y w= ℘(z), entonces la integral a largo de la curva Γ la podremos expresar por

${\displaystyle z-z_0={\displaystyle \underset{w_0}{\overset{w}{\int }}\frac{dt}{\sqrt{4t^3-g_{2}t-g_3}}}.}$

Esta integral es una función multiforme de w, pues el valor de la integral a lo largo de distintos caminos Γ que unen w₀ con w siempre será el mismo cuando los caminos pertenecen a un mismo recinto simplemente conexo que no contenga a los puntos singulares de la función subintegral e₁, e₂ y e₃ (en cada uno de estos puntos se anula).

Sin embargo, no se puede afirmar que los valores de las integrales sean iguales para dos caminos entre los cuales esté situado uno ó varios puntos e_j (j=1, 2, 3) ya que para un mismo valor de w=℘(z) le corresponde un conjunto infinito de valores distintos de z.
Todos los que cumplen

${\displaystyle z=\pm z\text{'}+2m{\omega }_1+2n{\omega }_3,}$

donde z' es alguno de los w-puntos de la función ℘(z) y m y n son números enteros cualesquiera.

Cuando z₀ tiende a cero w₀=℘(z₀) tiende a ∞ y como la integral

${\displaystyle {\displaystyle \underset{\infty }{\overset{w}{\int }}\frac{dt}{\sqrt{4t^3-g_{2}t-g_3}}}}$

es convergente, tenemos

${\displaystyle z={\displaystyle \underset{\infty }{\overset{w}{\int }}\frac{dt}{\sqrt{4t^3-g_{2}t-g_3}}}.}$

En esta igualdad w=℘(z) y el valor de la raíz cuadrada $\sqrt{4t^3-g_{2}t-g_3}$ tiene que coincidir con ℘'(z). Luego, de todo esto, deducimos que la función ℘(z) es inversa respecto de dicha integral.

${\displaystyle z={\displaystyle \underset{\infty }{\overset{w}{\int }}\frac{dt}{\sqrt{4t^3-g_{2}t-g_3}}}.}$

la denominaremos integral elíptica de primera especie en la forma normal de Weierstrass.