Péndulo esférico

Se denomina así a un punto material que se mueve sin rozamiento sobre la superficie de una esfera.

Elijamos un sistema de coordenadas cilíndrico. Entonces la ecuación de la esfera se puede expresar por:

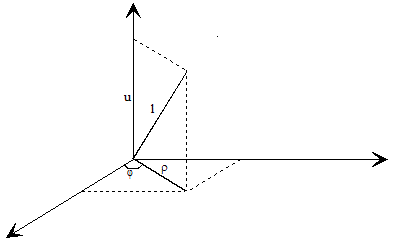
ρ²+u²=l², donde l es el radio de la esfera. Como el péndulo está bajo la acción de la fuerza de la gravedad -mg y la reacción normal de la esfera, según el teorema de las fuerzas vivas, aplicado al péndulo, tendremos:

${\displaystyle \frac{m{V}^2}{2}-\frac{m{V}_0{}^2}{2}=-mg(u-u_0)}$

es decir

V²=-2gu+h, donde h es una constante

Por otra parte, como las fuerzas que actúan sobre el péndulo siempre están situadas en un plano con el eje u, se puede aplicar el teorema de las áreas, el cual afirma que la velocidad areolar del movimiento de la proyección del péndulo sobre el plano u=0 respecto del origen de coordenadas se mantiene constante:

${\displaystyle {\rho }^2\frac{d\phi }{dt}=C}$

De esto, deducimos que el ángulo φ es una función monótona del tiempo t. Las ecuaciones anteriores nos van a determinar las coordenadas u, ρ y φ del punto móvil en función del tiempo.

Demostraremos que estas coordenadas se expresan mediante las funciones ℘, ζ, σ

Cálculo de u, para ello eliminamos φ y ρ en las ecuaciones anteriores.

${\displaystyle \rho =\sqrt{l^2-u^2}\frac{d\phi }{dt}=\frac{C}{{\rho }^2}}$

y

${\displaystyle V^2=\frac{d{s}^2}{d{t}^2}={\left[\frac{d\rho }{dt}\right]}^2+{\rho }^2{\left[\frac{d\phi }{dt}\right]}^2+{\left[\frac{du}{dt}\right]}^2}$

de

${\displaystyle V^2=-2gu+h\Rightarrow \frac{u^{2}u{\text{'}}^2}{l^2-u^2}+\frac{C^2}{l^2-u^2}+u{\text{'}}^2=-2gu+h}$

donde du/dt=u'. De aquí

${\displaystyle l^{2}u{\text{'}}^2=(h-2gu)(l^2-u^2)-C^2=q(u)}$

donde q(u) es un polinomio de tercer grado.

Si u₀(-l<u₀<l) es la coordenada del péndulo en el momento inicial, entonces, tendremos que tener: q(u₀))≥0, ya que la velocidad

${\displaystyle u\text{'}=\pm \frac{\sqrt{q(u)}}{l}}$

es un número real

Observando que

${\displaystyle q(+\infty )=+\infty ,q(l)=-C^2<\mathrm{0,}q(u_0)\ge \mathrm{0,}q(-l)=-C^2<0yq(-\infty )=-\infty }$

concluimos que todos los ceros u₁, u₂, u₃ del polinomio de tercer grado q(u) son reales.

Si q(u₀)>0, entonces los ceros están situados en los intervalos (l, +∞), (u₀, l) y (-l, u₀), uno en cada intervalo. Supongamos el siguiente orden:

${\displaystyle -l<u_3<u_0<u_2<l<u_1}$

Si q(u₀)=0, entonces en el intervalo (l, +∞) habrá un cero u₁ de forma que el número total de éstos en el mismo será impar, mientras que el intervalo (-∞, -l) no contendrá ningún cero. Por lo tanto, dos ceros tienen que estar situados en uno de los semiintervalos (-l, u₀] ó [u₀,l) y resulta la misma disposición que antes, con la sola diferencia que entre u₀ y u₃ o entre u₀ y u₂ aparece el signo de igualdad. En particular, es posible el caso en que

u₂=u₃=u₀

Entonces q(u)=2q(u-u₁)(u-u₀)² y la ecuación

${\displaystyle l^{2}u{\text{'}}^2=(h-2gu)(l^2-u^2)-C^2=q(u)}$

es integrable en funciones elementales.

A continuación, vamos a suponer que todas las raíces de la ecuación q(u)=0 son simples. En este caso q(u) se mantiene no negativo en el segmento [u₃, u₂], que contiene el valor u₀, y cambia de signo al pasar u por la frontera de este segmento. De aquí, deducimos que durante todo el tiempo del movimiento la coordenada u tiene que satisfacer las desigualdades

${\displaystyle -l<u_3\le u\le u_2<l}$

es decir, el péndulo se mantiene todo el tiempo dentro de cierto segmento esférico.

Volviendo a la ecuación

${\displaystyle l^{2}u{\text{'}}^2=(h-2gu)(l^2-u^2)-C^2=q(u)}$

y haciendo la sustitución u=av+b donde a≠0 y b son coeficientes reales. Tenemos,

${\displaystyle a^2{l}^{2}v{\text{'}}^2=q(av+b)\Rightarrow v{\text{'}}^2=\frac{1}{a^2{l}^2}q(av+b).}$

Elijamos a y b de modo que el polinomio

${\displaystyle \frac{1}{a^2{l}^2}q(av+b)\text{tome la forma }4v^3-g_{2}v-g_3.}$

Para ello, es suficiente igualar a cuatro el coeficiente superior del polinomio e igualar a cero el coeficiente de v². Entonces

${\displaystyle a=\frac{2l^2}{g},b=\frac{h}{6g}}$

y la ecuación queda de la forma

${\displaystyle v{\text{'}}^2=4v^3-g_{2}v-g_3.}$

Los ceros del polinomio 4v³-g₂v-g₃, son

${\displaystyle e_j=\frac{u_i-b}{a}(j=\mathrm{1,2,3})}$

donde e₁>e₂>e₃ puesto que u₁>u₂>u₃ y a>0. Al segmento u₃≤u≤u₂ le corresponde ahora el segmento e₃≤v≤e₂.
De aquí, se deduce que el discriminante

${\displaystyle \Delta =g_2{}^3-27g_3{}^2>0}$

y por lo tanto, por lo visto anteriormente, sabemos que existe una función elíptica ℘(z) con los periodos fundamentales: uno real 2α y el otro imaginario puro 2i·β, que cumple

${\displaystyle {\left[\wp \text{'}(\tau )\right]}^2=4{\left[\wp (\tau )\right]}^3-g_2\wp (\tau )-g_3.}$

Los periodos 2α y 2i·β se calculan mediante

${\displaystyle \alpha ={\displaystyle \underset{e_1}{\overset{+\infty }{\int }}\frac{d\lambda }{\sqrt{4{\lambda }^3-g_2\lambda -g_3}}}\beta ={\displaystyle \underset{-\infty }{\overset{e_3}{\int }}\frac{d\lambda }{\sqrt{-(4{\lambda }^3-g_2\lambda -g_3)}}.}}$

Si τ=σ+i·β, entonces como ya vimos ℘(τ)=℘(σ+i·β) es una función de σ de periodo 2α, la cual es diferenciable y creciente desde e₃ hasta e₂ en el segmento [0, α] y decreciente desde e₂ hasta e₃ en el segmento [α, 2α]. Los mismos valores toma también ℘(τ) en cualquier recta τ=σ+(2k+1)i·β (k=0, ±1, ±2,...) . Hagamos la sustitución v=℘(σ+i·β) en la ecuación

${\displaystyle v{\text{'}}^2=4v^3-g_{2}v-g_3}$

Tenemos

${\displaystyle {\left[\frac{d\wp (\sigma +i\beta )}{d\sigma }\right]}^2{\left[\frac{d\sigma }{dt}\right]}^2=4{\left[\wp (\sigma +i\beta )\right]}^3-g_2\wp (\sigma +i\beta )-g_3}$

de donde

${\displaystyle {\left[\frac{d\sigma }{dt}\right]}^2=1\Rightarrow \sigma =\pm (t-t_0)}$

donde ±t₀ es la constante de integración y, por consiguiente,

${\displaystyle v=\wp \left[\pm (t-t_0)+i\beta \right]}$

Como

${\displaystyle \wp (-\sigma +i\beta )=\wp (\sigma -i\beta )=\wp (\sigma +i\beta )}$

la elección del signo en el resultado obtenido es indiferente. Tomaremos

${\displaystyle v=\wp \left[(t-t_0)+i\beta \right]}$

de modo que para t=t₀, ℘(i·β)=e₃=min v. Calcularemos el tiempo t desde este momento, entonces tendremos

${\displaystyle v=\wp (t+i\beta )\text{y}u=av+b=\frac{2l^2}{g}\wp (t+i\beta )+\frac{h}{g}.}$

Luego, la ecuación

${\displaystyle l^{2}u{\text{'}}^2=(h-2gu)(l^2-u^2)-C^2=q(u)}$

está resuelta.

Conclusión

Nos ha resultado que u es una función periódica de t, de periodo 2α, y se expresa mediante una función elíptica ℘. Además alcanza el valor mínimo u₃ para t=0, 2α, 4α... y el valor máximo u₂ en t=0, α, 3α...

Ahora vamos a calcular el ángulo φ=φ(t) para ello expresemos dφ en la forma

${\displaystyle d\phi =\frac{Cdt}{l^2-u^2}=\frac{Cdt}{2l}\left(-\frac{1}{u-l}+\frac{1}{u+l}\right).}$

La función u=a℘(τ)+b toma los valores ±l para

${\displaystyle \wp (\tau )=\frac{\pm l-b}{a}}$

Pero

${\displaystyle \frac{l-b}{a}>\frac{u_2-b}{a}=e_{2}y\frac{-l-b}{a}<\frac{u_3-b}{a}=e_3.}$

Luego el valor de τ que satisface a la condición

${\displaystyle u=a\wp (\tau )+b=l}$

puede expresarse en la forma

${\displaystyle \tau =\alpha +i\gamma }$

y el valor de τ que satisface la condición

${\displaystyle u=a\wp (\tau )+b=-l}$

en la forma

${\displaystyle \tau =i\delta }$

donde γ y τ son números reales.

Así, pues

${\displaystyle u-l=a\left[\wp (t)-\wp (\alpha +i\gamma )\right],u+l=a\left[\wp (t)-\wp (i\delta )\right]}$

y

${\displaystyle d\phi =\frac{Cdt}{2al}\left[-\frac{1}{\wp (t)-\wp (\alpha +i\gamma )}+\frac{1}{\wp (t)-\wp (i\delta )}\right].}$

Para calcular aquí la constante C, observamos que como l²u'²-q(u) es una función meromorfa de u, la cual se anula para todos los 0≤t<∞, o sea, para todos los u del segmento u₃≤u≤u₂, resulta que, en virtud del teorema de unicidad para las funciones analíticas, ésta es idénticamente igual a cero. Por lo tanto, para cualquier número complejo τ tenemos

${\displaystyle l^{2}u{\text{'}}^2-q(u)=a^2{l}^2\wp {\text{'}}^2(\tau )-q\left[a\wp (\tau )+b\right]=0}$

y

${\displaystyle l^{2}u{\text{'}}^2=(h-2gu)(l^2-u^2)-C^2=q(u)}$

luego

${\displaystyle a^2{l}^2{\left[\wp \text{'}(\alpha +i\gamma \right]}^2=q(l)=-C^2}$

y

${\displaystyle a^2{l}^2{\left[\wp \text{'}(i\delta )\right]}^2=q(-l)=-C^2}$

De aquí que

${\displaystyle {\left[\wp \text{'}(\alpha +i\gamma )\right]}^2={\left[\wp \text{'}(i\delta )\right]}^2=-\frac{C^2}{a^2{l}^2}}$

Como

${\displaystyle \wp (\alpha +i\gamma )=\wp (-\alpha -i\gamma )=\wp (\alpha -i\gamma )=l}$

y

${\displaystyle \wp (i\delta )=\wp (-i\delta )=-l}$

mientras que

${\displaystyle \wp \text{'}(\alpha +i\gamma )=-\wp \text{'}(-\alpha -i\gamma )=-\wp \text{'}(\alpha -i\gamma )}$

y

${\displaystyle \wp \text{'}(i\delta )=-\wp \text{'}(-i\delta )}$

podemos elegir los valores de γ y δ de forma que se cumplan las igualdades

${\displaystyle \wp \text{'}(\alpha +i\gamma )=\wp \text{'}(i\delta )=\frac{iC}{al}}$

junto con ℘(α+i·γ)=l y ℘(i·δ)=-l. Entonces la ecuación

${\displaystyle d\phi =\frac{Cdt}{2al}\left[-\frac{1}{\wp (t)-\wp (\alpha +i\gamma )}+\frac{1}{\wp (t)-\wp (i\delta )}\right]}$

se puede poner como

${\displaystyle 2i\frac{d\phi }{dt}=\frac{\wp \text{'}(i\delta )}{\wp (t)-\wp (i\delta )}-\frac{\wp \text{'}(\alpha +i\gamma )}{\wp (t)-\wp (\alpha +i\gamma )}}$

y utilizando la fórmula

${\displaystyle \frac{\wp \text{'}(z)}{\wp (z)-\wp (t)}=\zeta (z+t)+\zeta (z-t)-2\zeta (z)}$

tenemos

${\displaystyle 2i\frac{d\phi }{dt}=-\zeta (i\delta +t)-\zeta (i\delta -t)+2\zeta (i\delta )+\zeta (\alpha +i\gamma +t)+\zeta (\alpha +i\gamma -t)-2\zeta (\alpha +i\gamma )}$

de done

${\displaystyle 2i\phi =\left\{\begin{array}{l}\ln A-\ln \sigma (t+i\delta )+\ln \sigma (t-i\delta )+2\zeta (i\delta )t+\ln \sigma (t+\alpha +i\gamma )\\ -\ln \sigma (t-\alpha -i\gamma )-2\zeta (\alpha +i\gamma )t\end{array}\right\}}$

luego

${\displaystyle e^{2i\phi }=A\frac{\sigma (t+\alpha +i\gamma )\sigma (t-i\delta )}{\sigma (t-\alpha -i\gamma )\sigma (t+i\delta )}\exp 2\left[\zeta (i\delta )-\zeta (\alpha +i\gamma )\right]t}$

Para t=0 resulta e^2iφ₀=A, por lo tanto,

${\displaystyle e^{2i(\phi -{\phi }_0)}=\frac{\sigma (t+\alpha +i\gamma )\sigma (t-i\delta )}{\sigma (t-\alpha -i\gamma )\sigma (t+i\delta )}\exp 2\left[\zeta (i\delta )-\zeta (\alpha +i\gamma )\right]t}$

Esta fórmula junto con

${\displaystyle u=av+b=\frac{2l^2}{g}\wp (t+i\beta )+\frac{h}{g}}$

nos resuelven completamente el problema del movimiento del péndulo esférico.