Problema de la inversión de las integrales elípticas

Se trata de demostrar que la función inversa de la integral elíptica

$z = \int_{\infty}^{w} \frac{d t}{\sqrt{4 t^{3} - g'' t - g'''}}$

es una función elíptica w=℘(z) con los invariantes g'' y g''' .
El problema lo tendremos resuelto si demostramos que existen unos números complejos 2ω' y 2ω'', cuya razón no sea un número real y que cumplan las ecuaciones:

$g'' = 60 \sum_{Ω \neq 0} \frac{1}{{(2 m ω' + 2 n ω'')}^{4}}, g''' = 140 \sum_{Ω \neq 0} \frac{1}{{(2 m ω' + 2 n ω'')}^{6}},$

siendo Ω=2mω'+2nω'' .

Veamos, si construimos una función ℘(z) de periodos fundamentales 2ω' y 2ω'', podremos afirmar que sus invariantes coinciden con los números dados g'' y g''' y por tanto, satisfacen la ecuación diferencial dada.

Nos vamos a limitar a resolver el problema en el caso más sencillo cuando g'' y g'' son números reales. Distinguiremos dos casos:

Cuando

$Δ = \frac{1}{16} [{(g'')}^{3} - 27 {(g''')}^{2}] > 0$

entonces todas las raíces de la ecuación

$4 t^{3} - g'' t - g''' = 0$

son reales y distintas.
Sean e', e'' y e''' dichas raíces, las vamos a elegir con la condición de que e'> e''>e''', luego

$4 t^{3} - g'' t - g''' = 4 (t - e') (t - e'') (t - e''')$

toma valores reales para t real y, además, positivos cuando t>e' y negativos cuando t<e'''. Si hacemos

$\begin{array}{l} ω' = \int_{+ \infty}^{e'} \frac{d t}{- \sqrt{4 t^{3} - g'' t - g'''}} = \int_{e'}^{+ \infty} \frac{d t}{2 \sqrt{(t - e') (t - e'') (t - e''')}} \\ ω'' = \int_{+ \infty}^{e'''} \frac{d t}{- i \sqrt{- 4 t^{3} + g'' t + g'''}} = i \int_{- \infty}^{e'''} \frac{d t}{2 \sqrt{- (t - e') (t - e'') (t - e''')}} \end{array}$

tenemos que ω' es un número real positivo, mientras que ω'' es un número imaginario puro con su parte imaginaria positiva.
Con todo esto, vamos hacer que ω' y ω'' sean los semiperiodos de la función elíptica ℘(z) y demostraremos, entonces, que esta función es la solución del problema planteado.

Veamos, haciendo

$t = e''' + \frac{e' - e'''}{u^{2}} con u > 0$

t→∞ entonces u→0 y cuando t→e', u→1

La primera integral nos quedará

$ω' = \int_{1}^{0} \frac{\frac{- 2 (e' - e''')}{u^{3}} d u}{2 \sqrt{[e''' + \frac{e' - e'''}{u^{2}} - e']} [e''' + \frac{e' - e'''}{u^{2}} - e''] [e''' + \frac{e' - e'''}{u^{2}} - e''']} .$

Si llamamos

$A = \frac{e' - e'''}{u^{2}}$

el radicando nos queda

$\begin{array}{l} [(e''' - e') + A] [(e''' - e'') + A] A = [- A u^{2} + A] [(e''' - e'') + A] A = \\ = A (1 - u^{2}) [\frac{u^{2} (e''' - e'') A}{e' - e'''} + A] A = A^{3} (1 - u^{2}) [1 - \frac{u^{2} (e'' - e''')}{e' - e'''}] \end{array}$

y la integral

$\begin{array}{l} ω' = \int_{1}^{0} \frac{- \frac{e' - e'''}{u^{3}} d u}{\frac{1}{u^{3}} \sqrt{{(e' - e''')}^{3} (1 - u^{2}) [1 - \frac{e'' - e'''}{e' - e'''} u^{2}]}} = \\ = \frac{1}{\sqrt{e' - e'''}} \int_{0}^{1} \frac{d u}{\sqrt{(1 - u^{2}) (1 - k^{2} u^{2})}} \end{array}$

siendo

$0 < k^{2} = \frac{e'' - e'''}{e' - e'''} < 1$

En la segunda integral sustituimos t por -t

$ω'' = \frac{i}{2} \int_{\infty}^{- e'''} \frac{- d t}{\sqrt{(t + e') (t + e'') (t + e''')}} = \frac{i}{2} \int_{- e'''}^{\infty} \frac{d t}{\sqrt{(t + e') (t + e'') (t + e''')}}$

hacemos

$t = \frac{e' - e'''}{u^{2}} - e' con u > 0$

cuando t→-e''' entonces u→1 y cuando t→∞, u→0

$ω'' = \frac{i}{2} \int_{1}^{0} \frac{- 2 \frac{e' - e'''}{u^{3}} d u}{\sqrt{[\frac{e' - e'''}{u^{2}} - e' + e'] [\frac{e' - e'''}{u^{2}} - e' + e''] [\frac{e' - e'''}{u^{2}} - e' + e''']}}$

operando, como anteriormente, el radicando, llamando

$B = \frac{e' - e'''}{u^{2}}$

tenemos

$\begin{array}{l} B (B + e'' - e') (B + e''' - e') = B (B + e'' - e') (B - B u^{2}) = \\ B^{2} (1 - u^{2}) [B + B \frac{e'' - e'}{e' - e'''} u^{2}] = B^{3} (1 - u^{2}) [1 + \frac{e'' - e'}{e' - e'''} u^{2}] \end{array}$

luego

$\begin{array}{l} ω'' = i \int_{0}^{1} \frac{\frac{e' - e'''}{u^{3}} d u}{\frac{1}{u^{3}} \sqrt{{(e' - e''')}^{3} (1 - u^{2}) [1 - \frac{u^{2} (e' - e'')}{e' - e'''}]}} = \\ = \frac{i}{\sqrt{e' - e'''}} \int_{0}^{1} \frac{d u}{\sqrt{(1 - u^{2}) [1 - \frac{u^{2} (e' - e'')}{e' - e'''}]}} = \frac{i}{\sqrt{e' - e'''}} \int_{0}^{1} \frac{d u}{\sqrt{(1 - u^{2}) (1 - k'^{2} u^{2})}} \end{array}$

siendo

$0 < k'^{2} = \frac{e' - e''}{e' - e'''} = 1 - k^{2} < 1$

De las fórmulas obtenidas se deduce que

$\frac{i ω'}{ω''} = \frac{\int_{0}^{1} \frac{d u}{\sqrt{(1 - u^{2}) (1 - k^{2} u^{2})}}}{\int_{0}^{1} \frac{d u}{\sqrt{(1 - u^{2}) (1 - k'^{2} u^{2})}}}$

Cuando k² crece desde 0 hasta 1, la integral que figura en el numerador crece desde

$\int_{0}^{1} \frac{d u}{\sqrt{1 - u^{2}}} = \frac{π}{2}$

hasta

${\int_{0}^{1} \frac{d u}{1 - u^{2}} = \frac{1}{2} \ln [\frac{1 + u}{1 - u}] |}_{0}^{1} = \infty$

En este caso k'²=1-k² decrece desde 1 hasta 0 y, por consiguiente, el denominador decrece desde infinito hasta π/2. Luego la razón i·ω'/ω'' crece desde 0 hasta infinito, pasando por todos los valores positivos cuando

$k^{2} = \frac{e'' - e'''}{e' - e'''}$

crece desde 0 hasta 1.
Por esta razón, a cualquier valor de i·ω'/ω'', dado a priori, le corresponde un valor y sólo uno, de k² comprendido entre 0 y 1.

Hallando k² por los valores dados de ω' y ω'', de la fórmula

$\sqrt{e' - e'''} = \frac{1}{ω'} \int_{0}^{1} \frac{d u}{\sqrt{(1 - u^{2}) (1 - k^{2} u^{2})}}$

obtenemos e'-e'''. También podemos suponer conocido

$e'' - e''' = (e' - e''') k^{2}$

y, finalmente, de la relación e'+e''+e'''=0, hallamos cada uno de los números e', e'' y e'''.

En resumen, dando a priori los valores de las integrales

$ω' = \int_{+ \infty}^{e'} \frac{d t}{- \sqrt{4 t^{3} - g'' t - g'''}} y ω'' = i \int_{- \infty}^{e'''} \frac{d t}{\sqrt{- (4 t^{3} - g'' t - g''')}}$

(con la condición de que ω' y ω''/i sean números positivos), podemos obtener unívocamente los valores de las raíces e', e'' y e''' de la ecuación

$4 t^{3} - g'' t - g''' = 0$

y, por lo tanto, también los valores de los coeficientes g'' y g'''. Utilizaremos esto, para demostrar que los invariantes g₂ y g₃ de la función construida ℘(z) coinciden con los números g'' y g''', con lo cual terminamos la resolución del problema de inversión en el caso considerado.

Anteriormente, ya habíamos estudiado que cuando la función ℘(z) tenía un periodo real y otro imaginario puro, entonces w=℘(z) tomaba valores reales y decrecía desde infinito hasta e₁=℘(ω') cuando a lo largo del eje real se variaba desde 0 hasta ω'.

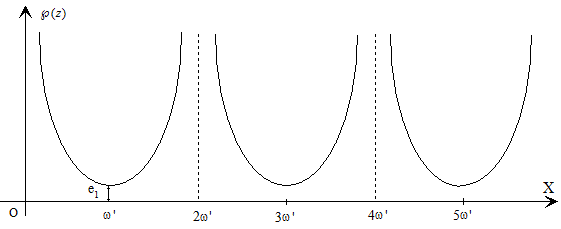
Designando con g₂ y g₃ los invariantes de la función ℘(z) y observando que ℘'(z) toma valores reales negativos para 0<z=x <ω', obtenemos:

$℘' (x) = - \sqrt{4 {[℘ (x)]}^{3} - g_{2} ℘ (x) - g_{3}}$

de donde

$ω' = \int_{- \infty}^{e_{1}} \frac{d t}{- \sqrt{4 t^{3} - g_{2} t - g_{3}}}$

También habíamos visto que ℘(z) tomaba valores reales y crecía desde -∞ hasta e₃ cuando z=i·y variaba desde 0 hasta ω'' a lo largo del eje imaginario.

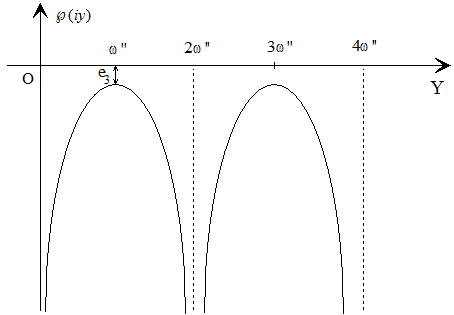
Además, la derivada

$\frac{d ℘ (z)}{d z} = - i \frac{d ℘ (i y)}{d y}$

toma valores imaginarios puros con partes imaginarias negativas. Luego para z=i·y donde 0<y<ω''/i, tenemos

$℘' (i y) = - i \sqrt{- {4 {[℘ (i y)]}^{3} - g_{2} ℘ (i y) - g_{3}}}$

de donde

$ω'' = i \int_{+ \infty}^{e_{3}} \frac{d t}{\sqrt{- (4 t^{3} - g_{2} t - g_{3})}}$

Pero, según lo demostrado, los valores de los coeficientes del polinomio que está en el radicando se determinan unívocamente por los valores de las integrales

$\begin{array}{l} ω' = \int_{+ \infty}^{e'} \frac{d t}{- \sqrt{4 t^{3} - g'' t - g'''}} = \int_{+ \infty}^{e_{1}} \frac{d t}{- \sqrt{4 t^{3} - g_{2} t - g_{3}}} \\ ω'' = i \int_{- \infty}^{e'''} \frac{d t}{- \sqrt{4 t^{3} - g'' t - g'''}} = i \int_{+ \infty}^{e_{3}} \frac{d t}{\sqrt{- (4 t^{3} - g_{2} t - g_{3})}} \end{array}$

Luego, g₂=g'' y g₃=g''' con lo cual terminamos la demostración para este caso.

Cuando

$Δ = \frac{1}{16} {{(g'')}^{3} - 27 {(g''')}^{2}} < 0.$

Aquí la ecuación

$4 t^{3} - g'' t - g''' = 0$

tiene que tener una raíz real e'' y dos raíces imaginarias conjugadas e' y e'''.
Vamos a elegir las notaciones de forma que la parte imaginaria de la raíz e''' sea positiva.

El polinomio

$4 t^{3} - g'' t - g''' = 4 (t - e') (t - e'') (t - e''')$

toma valores reales para t real y, además, positivos si t>e'' y negativos si t< e'', hagamos:

$\begin{array}{l} α = \int_{+ \infty}^{e''} \frac{d t}{- \sqrt{4 t^{3} - g'' t - g'''}} = \int_{e''}^{\infty} \frac{d t}{\sqrt{4 t^{3} - g'' t - g'''}} \\ y \\ β i = \int_{- \infty}^{e''} \frac{d t}{- i \sqrt{- (4 t^{3} - g'' t - g''')}} = i \int_{- \infty}^{e''} \frac{d t}{\sqrt{- (4 t^{3} - g'' t - g'''})} \end{array}$

Aquí α y β son números reales y positivos.

Ahora vamos a construir una función elíptica ℘(z) de periodos

$2 ω' = α - i β y 2 ω'' = α + i β$

y demostraremos que ésta es la solución del problema de inversión planteado, es decir que posee los invariantes g'' y g'''.
Para ello realizamos el cambio de variable

$t = e'' + u^{2}, u > 0$

en las integrales anteriores, obteniendo

$\begin{array}{l} α = \int_{0}^{\infty} \frac{2 u d u}{2 \sqrt{(e'' + u_{2} - e') (e'' + u_{2} - e'') (e'' + u_{2} - e''')}} = \\ = \int_{0}^{\infty} \frac{u d u}{\sqrt{u_{2} (u_{2} + e'' - e') (u_{2} + e'' - e''')}} \end{array}$

haciendo

$e'' - e' = ρ e^{i ϕ} entonces e'' - e''' = ρ e^{- i ϕ} donde 0 < ϕ < π$

y por lo tanto

$α = \int_{0}^{\infty} \frac{d u}{\sqrt{(u^{2} + ρ e^{i ϕ}) (u^{2} + ρ e^{- i ϕ})}} = \int_{0}^{\infty} \frac{d u}{\sqrt{u^{4} + 2 u^{2} ρ \cos ϕ + ρ^{2}}}$

finalmente poniendo $u = \sqrt{ρ} t$

$α = \int_{0}^{\infty} \frac{\sqrt{ρ} d t}{ρ \sqrt{t^{4} + 2 t^{2} \cos ϕ + 1}} .$

En la segunda integral lo primero que vamos hacer es cambiar t por -t,

$β = \int_{+ \infty}^{- e''} \frac{- d t}{\sqrt{4 (t + e') (t + e'') (t + e''')}} = \int_{- e''}^{\infty} \frac{d t}{2 \sqrt{(t + e') (t + e'') (t + e''')}}$

a continuación,

$t = - e'' + u^{2}, u > 0$

sustituyendo

$\begin{array}{l} β = \int_{0}^{\infty} \frac{2 u d u}{2 \sqrt{(- e'' + u^{2} + e') (- e'' + u^{2} + e') (- e'' + u^{2} + e''')}} = \\ \int_{0}^{\infty} \frac{u d u}{\sqrt{u^{2} [u^{2} - (e'' - e')] [u^{2} - (e'' - e''')]}} \end{array}$

con el cambio

$e'' - e' = ρ e^{i ϕ} entonces e'' - e''' = ρ e^{- i ϕ} donde 0 < ϕ < π$

$β = \int_{0}^{\infty} \frac{d u}{\sqrt{[u^{2} - ρ e^{i ϕ}] [u^{2} - ρ e^{- i ϕ}]}} = \int_{0}^{\infty} \frac{d u}{\sqrt{u^{4} - 2 u^{2} ρ \cos ϕ + ρ^{2}}}$

poniendo finalmente $u = \sqrt{ρ} t$

$β = \int_{0}^{\infty} \frac{\sqrt{ρ} d t}{ρ \sqrt{t^{4} - 2 t^{2} \cos ϕ + 1}}$

De las fórmulas halladas, se deduce que

$\frac{α}{β} = \frac{\int_{0}^{\infty} \frac{d t}{\sqrt{t^{4} + 2 t^{2} \cos ϕ + 1}}}{\int_{0}^{\infty} \frac{d t}{\sqrt{t^{4} - 2 t^{2} \cos ϕ + 1}}} .$

Si ø varia desde 0 hasta π su coseno decrece desde 1 a -1 y la integral del numerador crece desde

$\int_{0}^{\infty} \frac{d t}{1 + t^{2}} = \frac{π}{2}$

hasta el infinito y la integral del denominador decrece desde infinito hasta π/2. De aquí deducimos que la razón α/β crece desde 0 hasta infinito y, por consiguiente, a cada valor de ésta razón, dado a priori, le corresponde un único valor ø comprendido entre 0 y π.
Calculando ø mediante los valores dados de α y β y poniéndolo en la expresión de α, hallamos :

$\sqrt{ρ} = \frac{1}{α} \int_{0}^{\infty} \frac{d t}{\sqrt{t^{4} + 2 t^{2} \cos ϕ + 1}} .$

Por lo tanto, los valores de ρ y ø se determinan unívocamente por los valores de α y β. Luego las diferencias e''-e' y e''-e''' también y mediante la relación e'+e''+e'''=0 las tres raíces de la ecuación

$4 t^{3} - g'' t - g''' = 0$

y finalmente, sus coeficientes g' y g'''.

Resumiendo, dando a priori los valores de las integrales

$α = \int_{+ \infty}^{e''} \frac{d t}{- \sqrt{4 t^{3} - g'' t - g'''}} y β = \int_{- \infty}^{e''} \frac{d t}{\sqrt{- (4 t^{3} - g'' t - g''')}}$

(siendo α y β números positivos) podemos determinar unívocamente los coeficientes g'' y g''' del polinomio 4t³-g''t-g'''.
Utilizaremos esto, para demostrar que los invariantes g₂ y g₃ de la función que hemos construido coinciden con los números dados g'' y g'''.

Habíamos estudiado anteriormente, que cuando la función ℘(z) tenía un par de periodos fundamentales conjugados α+i·β y α-i·β entonces w=℘(z) tomaba valores reales y decrecía desde infinito hasta e₂=℘(α) cuando z=x recorría el eje real desde 0 hasta α.

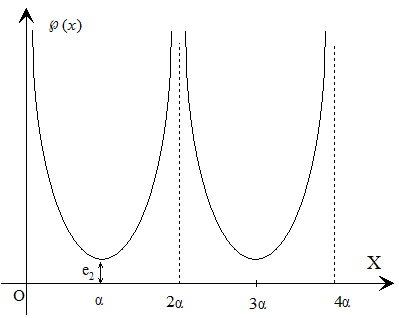
Observando que la derivada ℘'(z) tiene que tener en este caso valores reales negativos, obtenemos:

$℘' (x) = - \sqrt{4 {[℘ (x)]}^{3} - g_{2} ℘ (x) - g_{3}}$

de donde

$α = \int_{+ \infty}^{e_{2}} \frac{d t}{- \sqrt{4 t^{3} - g_{2} t - g_{3}}} .$

También vimos como la función ℘(z) toma valores reales y decrece desde e₂ hasta -∞ cuando z=a+i·y recorre el segmento de la recta paralela al eje imaginario desde el punto α hasta el punto α+i·β

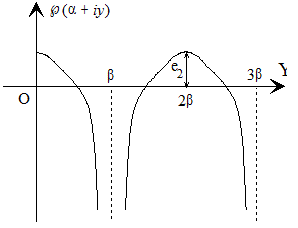
Además,

$\frac{d ℘ (z)}{d z} = - i \frac{d ℘ (α + i y)}{d y}$

toma valores imaginarios puros con la parte imaginaria positiva.
Luego, para z=α+i·y, donde 0<y<β

$℘' (α + i y) = i \sqrt{- {4 {[℘ (α + i y)]}^{3} - g_{2} ℘ (α + i y) - g_{3}}}$

de donde

$i β = (α + i β) - α = i \int_{- \infty}^{e_{2}} \frac{d t}{\sqrt{- (4 t^{3} - g_{2} t - g_{3})}}$

Como, según lo demostrado, los valores de los coeficientes del polinomio que está en el radicando se determinan de forma unívoca por los valores de las integrales consideradas

$\begin{array}{l} α = \int_{+ \infty}^{e''} \frac{d t}{- \sqrt{4 t^{3} - g'' t - g'''}} = \int_{+ \infty}^{e_{2}} \frac{d t}{- \sqrt{4 t^{3} - g_{2} t - g_{3}}} \\ β = \int_{- \infty}^{e''} \frac{d t}{\sqrt{- (4 t^{3} - g'' t - g'''})} = \int_{- \infty}^{e''} \frac{d t}{\sqrt{- (4 t^{3} - g_{2} t - g_{3}})} \end{array}$

deducimos que g₂=g'' y g₃=g''', con lo cual terminamos la demostración.

Conclusiones

De todo el estudio realizado se deduce, que si los invariantes g₂ yg₃ de la función ℘(z) son números reales, entonces ℘(z) posee un par de periodos fundamentales

uno real y el otro imaginario puro cuando el discriminante Δ es positivo,
conjugados cuando el discriminante Δ es negativo.

En cada uno de estos casos w=℘(z) representa la inversión de la integral elíptica

$z = \int_{\infty}^{w} \frac{d t}{\sqrt{4 t^{3} - g_{2} t - g_{3}}}$

cuyo par de periodos fundamentales para el caso (1) viene dado por:

$2 ω_{1} = \int_{\infty}^{e_{1}} \frac{d t}{- \sqrt{4 t^{3} - g_{2} t - g_{3}}} y 2 ω_{3} = \int_{- \infty}^{e_{3}} \frac{d t}{- i \sqrt{- (4 t^{3} - g_{2} t - g_{3})}}$

y para el caso (2) por:

$\begin{array}{l} α +i β = \int_{\infty}^{e_{2}} \frac{d t}{- \sqrt{4 t^{3} - g_{2} t - g_{3}}} + i \int_{- \infty}^{e_{2}} \frac{d t}{\sqrt{- (4 t^{3} - g_{2} t - g_{3})}} \\ α - i β = \int_{\infty}^{e_{2}} \frac{d t}{- \sqrt{4 t^{3} - g_{2} t - g_{3}}} - i \int_{- \infty}^{e_{2}} \frac{d t}{\sqrt{- (4 t^{3} - g_{2} t - g_{3})}} \end{array}$

Condición necesaria y suficiente

La condición necesaria y suficiente para que la función ℘(z) tome valores reales en el eje real es que los invariantes sean reales.

Necesaria

Si ℘(z) toma valores reales en el eje real, entonces

$4 {[℘ (z)]}^{3} - g_{2} ℘ (z) - g_{3} = {[℘' (z)]}^{2}$

también toma valores reales para z=x. Luego,

$℘ (x) Im g_{2} + Im g_{3} = 0$

para todos los valores reales de x, de donde

$Im g_{2} = Im g_{3} = 0$

por lo tanto g₂ y g₃ son números reales.

Suficiente

Si g₂ y g₃ son números reales, como hemos visto anteriormente ℘(z) ó posee un periodo fundamental real y el otro imaginario puro, o dos periodos fundamentales conjugados, en ambos casos la función ℘(z) toma valores reales en el eje real (y también en el imaginario).

Comparación de las funciones doblemente periódicas con las simplemente periódicas

Como analogía:

$\begin{array}{l} ℘ (z) {\begin{cases} Tiene un polo doble en cada uno de los periodos Ω =2m ω_{1} + 2 n ω_{3} . \\ La parte principal en el polo es 1/(z- Ω)^{2} \end{cases} \\ {cosec}^{2} z {\begin{cases} Tiene un polo doble en cada uno de sus periodos ω =n π . \\ La parte principal en el polo es 1/(z- ω)^{2} \end{cases} \end{array}$

Entre la funciones trigonométricas hay funciones más simples que cosec²(z) y que están estrechamente relacionadas con esta función, por ejemplo ctg(z) con polos simples en cada uno de los periodos ω y con las partes principales 1/(z-ω), y sin(z) con ceros simples en cada uno de los periodos. También tenemos la siguiente relación entre ellas:

$[ctg (z)]' = - {cosec}^{2} (z) y [\ln \sin (z)]' = ctg (z) .$

Entre las funciones elípticas no pueden existir funciones con polos simples en los periodos (y que no tengan otros polos más), ni funciones enteras. Sin embargo, sin exigir que sean elípticas, se pueden construir funciones que estén ligadas con ℘(z) del mismo modo que las funciones ctg(z) y sin(z) están ligadas con cosec²(z). Por ejemplo,