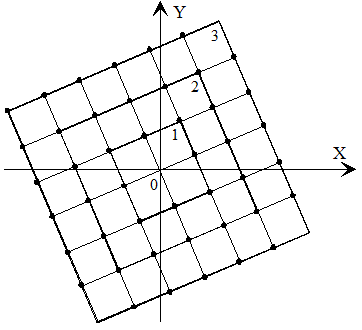
Sea f(z) una función meromorfa doblemente periódica. Sus periodos fundamentales los designaremos por 2ω₁, 2ω₃ y 2ω₂=2ω₁+2ω₃ representa el vértice del paralelogramo fundamental Δ que es opuesto al origen de coordenadas. El recorrido del contorno del paralelogramo de periodos correspondiente al orden de los vértices 0, 2ω₁, 2ω₂, ω₃, se efectuará en sentido contrario a las agujas del reloj, esto ocurre cuando la parte imaginaria del número complejo ω₃/ω₁ es mayor que cero.

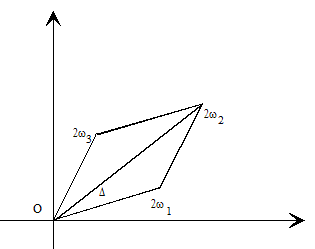
Veamos:

de nuestra elección geométrica si:

${\displaystyle \begin{array}{l}{\omega }_1=r_1{e}^{i{\theta }_1}{\omega }_3=r_3{e}^{i{\theta }_3}\\ \frac{{\omega }_3}{{\omega }_1}=\frac{r_3}{r_1}{e}^{i({\theta }_3-{\theta }_1)}=\frac{r_3}{r_1}{e}^{i\theta }\end{array}}$

Por tanto :

${\displaystyle \mathrm{Im}\left(\frac{{\omega }_3}{{\omega }_1}\right)=\frac{r_3}{r_1}\sin \theta >\mathrm{0,}\text{pues}\text{,}0<\theta <\pi .}$

Definición

Dos puntos distintos del plano z, z₁, z₂ diremos que son congruentes (respecto de los periodos 2ω₁, 2ω₃) si y solo si z₁-z₂=2mω₁+2pω₃ donde m y p son números enteros.

De la definición se deduce:

1. El paralelogramo de periodos no contiene ningún par de puntos congruentes.
2. Los puntos de sus lados y distintos de los vértices son congruentes entre sí.
3. Los puntos de los vértices forman una cuaterna de puntos congruentes entre sí.

A continuación vamos a adjuntar a cada paralelogramo Δ_m1m2 con los vértices 2m₁ω₁+2m₂ω₃, (2m₁+1)ω₁+2m₂ω₃, (2m₁+1)ω₁+(2m₂+1)ω₃, 2m₁ω₁+(2m₂+1)ω₃, su extremo inferior de la izquierda 2m₁ω₁+2m₂ω₃ y los puntos de los lados inferior e izquierdo, excluyendo de éstos sus extremos (2m₁+1)ω₁+2m₂ω₃ y 2m₁ω₁+(2m₂+1)ω₃. Debido a esto, queda adjuntado al paralelogramo solamente un punto de cada par o cuaterna de puntos del contorno congruentes entre sí. Este paralelogramo de periodos completado con estos puntos, igual que anteriormente lo representaremos por Δ_m1m2

Siendo z=2m₁ω₁+2m₂ω₃

Dicho paralelogramo tiene las siguientes propiedades:

1. Dos puntos cualesquiera distintos del paralelogramo Δ_m1m2 no son congruentes entre sí.
2. Para cada punto z' del plano, siempre hay un punto z y solo uno en el paralelogramo Δ_m1m2 congruente con z'.

Teorema 1

Si una función periódica esta definida en un paralelogramo fundamental, entonces está definida en todo el plano. (Se deduce de lo anterior).

Teorema 2

Si f(z) y g(z) son funciones elípticas con unos mismos periodos 2ω₁ y 2ω₃ entonces f(z)+g(z), f(z)-g(z), f(z)·g(z) y f(z)/g(z) (este último cuando g(z) no es idénticamente nulo) son funciones elípticas con los mismos periodos.

En general, si se efectúan operaciones racionales con funciones elípticas f₁(z), f₂(z),...f_n(z) que tengan los mismos periodos 2ω₁, 2ω₃ (excluyendo la división por una función idénticamente nula) se obtiene otra función elíptica con los mismos periodos.

Teorema 3

La derivada de una función elíptica es también una función elíptica y con los mismos periodos.

Demostración.- Primero f'(z) es meromorfa ya que la derivada de una función meromorfa es meromorfa.
Ahora escogemos un punto arbitrario z₁ donde f(z) es analítica y sea z₂ un punto congruente con z₁, entonces tenemos:

${\displaystyle \frac{f(z_1+\Delta z)-f(z_1)}{\Delta z}=\frac{f(z_2+\Delta z)-f(z_2)}{\Delta z}}$

Tomando límites cuando Δz→0, obtenemos

f'(z₁)=f'(z₂)

Luego f'(z) tiene los mismos periodos que f(z) y además no puede ser nunca una constante ya que entonces tendríamos f(z)=cz+d, que no es elíptica. En consecuencia el teorema.

Teorema 4

Una función elíptica f(z)≠const no puede ser entera.

Demostración.- Supongamos lo contrario, es decir que f(z) es entera, entonces en el paralelogramo cerrado de periodos es continúa y por tanto estará acotada.

|f(z)|<C

Sabemos que para cada punto del plano z' siempre existe un punto z y solo uno en el paralelogramo de periodos que es congruente con z', por lo tanto la función tomará en el punto z' el mismo valor que en el punto z y aplicando el teorema de Liouville llegamos a la conclusión de que f(z) es constante, lo cual es una contradicción.

Del teorema deducimos las siguientes:

Consecuencias

1. Si f(z) es una función elíptica no constante, entonces tiene al menos un polo en el paralelogramo de periodos.

2. El número total de polos pertenecientes a uno de los paralelogramos de periodos tiene que ser finito, pues en caso contrario tendríamos un punto de acumulación de polos en el paralelogramo cerrado de periodos.

3. La suma de los órdenes de todos los polos que pertenecen a un mismo paralelogramo de periodos no depende de la elección de los periodos fundamentales.

En efecto, dado el paralelogramo Δ, si consideramos otro Φ formado con otro par de periodos fundamentales:

2Ω₁=m2ω₁+n2ω₃    2Ω₃=p2ω₁+q2ω₃    mq-np=1

entonces a cada polo ø∈Φ corresponde un polo, y solo uno δ∈Δ congruente con él, y recíprocamente. Más aún, los órdenes de los polos ø y δ son iguales. Pues como f(z) es periódica, su desarrollo en serie de Laurent en un entorno del punto δ se convierte en el desarrollo en un entorno del punto ø mediante la sustitución de z-ø por z-δ sin que se alteren los coeficientes.

Definición

Llamaremos orden de la función f(z) a la suma de los órdenes de todos los polos que pertenecen a un paralelogramo fundamental.

Teorema 5

La suma de los residuos de una función elíptica f(z), respecto de todos los polos situados en el paralelogramo de periodos, es igual a cero.

Demostración.- Tendremos que comprobar que la integral de f(z) a lo largo de un circuito que contenga en su interior a todos los polos pertenecientes a uno de los paralelogramos de periodos Δ, y que no contenga a otros polos, es cero. Si en el contorno C del paralelogramo cerrado Δ no hay ningún polo de la función f(z), entonces éste nos sirve para la integración. Pero si en C hay polos, sustituiremos el circuito C por el contorno C' de un paralelogramo Δ' con los lados paralelos e iguales a los de Δ de modo que en C' no haya ningún polo de la función f(z), y en el interior de C' estén contenidos todos los polos pertenecientes a Δ. Esto se conseguirá desplazando C por la diagonal del paralelogramo Δ en dirección desde el vértice 2ω₂ hacia el vértice O en una magnitud menor que la distancia desde el conjunto de polos, pertenecientes a Δ hasta el conjunto de puntos pertenecientes al lado de la derecha y al lado superior. Los vértices del circuito de integración C' los denotaremos por: z₁, z₁+2ω₁, z₁+2ω₂, z₁+2ω₃.

${\displaystyle \begin{array}{l}\frac{1}{2\pi i}{\displaystyle \underset{C\text{'}}{\int }f(z)dz}=\\ \frac{1}{2\pi i}{\displaystyle \underset{z_1}{\overset{z_1+2{\omega }_1}{\int }}f(z)dz}+\frac{1}{2\pi i}{\displaystyle \underset{z_1+2\omega {}_1}{\overset{z_1+2{\omega }_2}{\int }}f(z)dz}+\frac{1}{2\pi i}{\displaystyle \underset{z_1+2\omega {}_2}{\overset{z_1+2\omega {}_3}{\int }}f(z)dz}+\frac{1}{2\pi i}{\displaystyle \underset{z_1+2{\omega }_3}{\overset{z_1}{\int }}f(z)dz}\end{array}}$

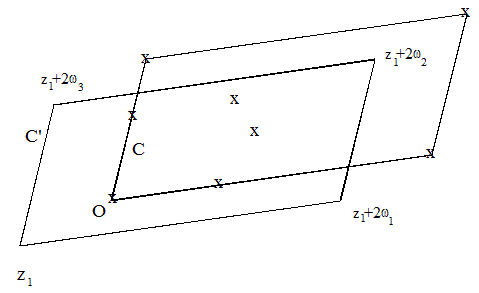
Vamos a demostrar que la suma de la primera y tercera integral vale cero así como la de la segunda y cuarta.

Si suponemos que la ecuación del lado que une los vértices z₁ y z₁+2ω₁ es

${\displaystyle z=z_1+2{\omega }_{1}t,0\le t\le 1}$

entonces

${\displaystyle \frac{1}{2\pi i}{\displaystyle \underset{z_1}{\overset{z_1+2{\omega }_1}{\int }}f(z)dz}=\frac{2{\omega }_1}{2\pi i}{\displaystyle \underset{0}{\overset{1}{\int }}f(z_1+2{\omega }_{1}t)dt}}$

La ecuación del lado que une los vértices z₁+2ω₃, z₁+2ω₂ será:

${\displaystyle z=z_1+2{\omega }_3+(2{\omega }_2-2{\omega }_3)t=z_1+2{\omega }_3+2{\omega }_{1}t,0\le t\le 1}$

y por tanto

${\displaystyle \begin{array}{l}\frac{1}{2\pi i}{\displaystyle \underset{z_1+2{\omega }_2}{\overset{z_1+2{\omega }_3}{\int }}f(z)dz}=-\frac{1}{2\pi i}{\displaystyle \underset{z_1+2{\omega }_3}{\overset{z_1+2{\omega }_2}{\int }}f(z)dz}=-\frac{2{\omega }_1}{2\pi i}{\displaystyle \underset{0}{\overset{1}{\int }}f(z_1+2{\omega }_3+2{\omega }_{1}t)dt=}\\ -\frac{2{\omega }_1}{2\pi i}{\displaystyle \underset{0}{\overset{1}{\int }}f(z_1+2{\omega }_{1}t)dt}\end{array}}$

Luego la suma de las dos integrales calculadas vale cero.

Del mismo modo demostraríamos que la suma de la segunda y la cuarta también vale cero. Por tanto

${\displaystyle \frac{1}{2\pi i}{\displaystyle \underset{C\text{'}}{\int }f(z)dz}=0}$

Con esto hemos demostrado que la suma de los residuos de la función f(z) respecto de todos los polos que están situados en el interior de C' vale cero .

Corolario.- No hay funciones elípticas de primer orden. Es decir, el orden de una función elíptica f(z)≠const no es menor que dos

Demostración.- Supongamos que no se cumple, esto es, f(z) posee en el paralelogramo de periodos un solo polo δ simple. Entonces en el desarrollo de Laurent de la función f(z) en un entorno del punto δ, su parte principal tiene la forma D/(z-δ) donde D es el residuo de la función f(z) respecto del punto δ

Pero según lo demostrado en el teorema anterior D y por tanto f(z) no tiene polos en el paralelogramo de periodos y según el teorema 4, f(z) será constante con lo cual llegamos a una contradicción.

Definición

Sea A un número complejo arbitrario. A las raíces de la ecuación f(z)=A las llamaremos A-puntos de la función f(z).

Teorema 6

El número de A-puntos de una función elíptica f(z)≠const, pertenecientes al paralelogramo de periodos, no depende de A y es igual al orden de la función elíptica (al menos es igual a dos).

Demostración.-

1. para A=∞ el teorema se deduce de la definición de orden de la función elíptica.

2. para A≠∞ si recordamos que la integral

${\displaystyle \frac{1}{2\pi i}{\displaystyle \int \frac{f\text{'}(z)}{f(z)-A}}dz}$

tomada en sentido positivo a lo largo del circuito que contiene en su interior a todos los polos y A-puntos pertenecientes a un paralelogramo de periodos, es igual a la diferencia entre el número de polos y A-puntos, entonces tendremos que demostrar que dicha integral vale cero .

Si en el contorno C del paralelogramo cerrado Δ no hay ningún polo ni A-puntos, entonces éste nos sirve para la integración. En caso contrario lo desplazaremos por la diagonal desde 2ω₂ hasta 0 de modo que todos los polos y A-puntos estén en el interior.

Si C' es el nuevo contorno (no contendrá ni polos ni A-puntos) entonces

${\displaystyle \frac{1}{2\pi i}{\displaystyle \underset{C\text{'}}{\int }\frac{f\text{'}(z)}{f(z)-A}dz}=0}$

pues como f(z) y f'(z) son elípticas con los mismos periodos, toda combinación racional

${\displaystyle \frac{f\text{'}(z)}{f(z)-A}=g(z)}$

también es elíptica y con los mismos periodos y como sabemos que la suma de los residuos de la función g(z), respecto de todos los polos situados en el paralelogramo de periodos vale cero, ya tenemos lo que buscábamos.

Teorema 7

La suma de todos los A-puntos de una función elíptica f(z)≠const, pertenecientes a un paralelogramo de periodos, es congruente a la suma de todos los polos, pertenecientes también a un paralelogramo de periodos.

Demostración.- Supongamos A≠∞ pues el caso A=∞ es evidente. Vamos a considerar el circuito C' que utilizamos en la demostración del teorema anterior y a continuación vamos a tomar la integral

${\displaystyle \frac{1}{2\pi i}{\displaystyle \underset{C\text{'}}{\int }z\frac{f\text{'}(z)}{f(z)-A}dz}}$

que como sabemos nos da la diferencia entre la suma de todos los A-puntos y la suma de todos los polos situados en el interior de C'. Entonces para demostrar el teorema tendremos que ver que dicha integral es igual a algún periodo de la función f(z).

${\displaystyle \begin{array}{l}\frac{1}{2\pi i}{\displaystyle \underset{C\text{'}}{\int }z\frac{f\text{'}(z)}{f(z)-A}dz}=\frac{1}{2\pi i}{\displaystyle \underset{z_1}{\overset{z_1+2\omega {}_1}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}+\frac{1}{2\pi i}{\displaystyle \underset{z_1+2\omega {}_1}{\overset{z_1+2\omega {}_2}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}-\\ -\frac{1}{2\pi i}{\displaystyle \underset{z_1+2\omega {}_3}{\overset{z_1+2\omega {}_2}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}-\frac{1}{2\pi i}{\displaystyle \underset{z_1}{\overset{z_1+2\omega {}_3}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}\end{array}}$

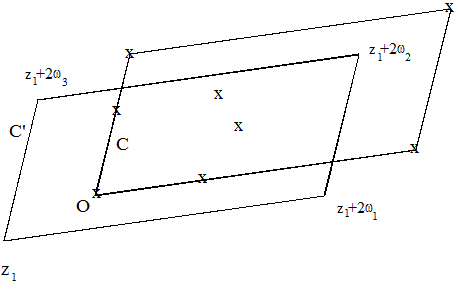
La ecuación del lado del circuito que va de z₁ a z₁+2ω₁ vendrá dada por:

${\displaystyle z=z_1+2{\omega }_{1}t,0\le t\le 1.}$

Por lo tanto

${\displaystyle \frac{1}{2\pi i}{\displaystyle \underset{z_1}{\overset{z_1+2\omega {}_1}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}=\frac{2{\omega }_1}{2\pi i}{\displaystyle \underset{0}{\overset{1}{\int }}(z_1+2{\omega }_{1}t)\frac{f\text{'}(z_1+2{\omega }_{1}t)}{f(z_1+2{\omega }_{1}t)-A}dz}.}$

La ecuación del lado del circuito que va de z₁+2ω₃ a z₁+2ω₂ vendrá dada por:

${\displaystyle z=z_1+2{\omega }_3+(2{\omega }_2-2{\omega }_3)t=z_1+2{\omega }_3+2{\omega }_{1}t,0\le t\le 1}$

entonces

${\displaystyle \begin{array}{l}-\frac{1}{2\pi i}{\displaystyle \underset{z_1+2\omega {}_3}{\overset{z_1+2\omega {}_2}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}=-\frac{2{\omega }_1}{2\pi i}{\displaystyle \underset{0}{\overset{1}{\int }}(z_1+2{\omega }_3+2{\omega }_{1}t)\frac{f\text{'}(z_1+2{\omega }_3+2{\omega }_{1}t)}{f(z_1+2{\omega }_3+2{\omega }_{1}t)-A}dt}=\\ =-\frac{2{\omega }_1}{2\pi i}{\displaystyle \underset{0}{\overset{1}{\int }}(z_1+2{\omega }_3+2{\omega }_{1}t)\frac{f\text{'}(z_1+2{\omega }_{1}t)}{f(z_1+2{\omega }_{1}t)-A}dt}\end{array}}$

Luego

${\displaystyle \begin{array}{l}\frac{1}{2\pi i}{\displaystyle \underset{z_1}{\overset{z_1+2\omega {}_1}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}-\frac{1}{2\pi i}{\displaystyle \underset{z_1+2{\omega }_3}{\overset{z_1+2\omega {}_1}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}=-\frac{2{\omega }_1}{2\pi i}2{\omega }_3{\displaystyle \underset{0}{\overset{1}{\int }}\frac{f\text{'}(z_1+2{\omega }_{1}t)}{f(z_1+2{\omega }_{1}t)-A}dt}=\\ =-\frac{2{\omega }_3}{2\pi i}{\left\{\ln \left[f(z_1+2{\omega }_{1}t)-A\right]\right\}}_0^1=-\frac{2{\omega }_3}{2\pi i}\ln \left[\frac{f(z_1+2{\omega }_1)-A}{f(z_1)-A}\right]=-\frac{2{\omega }_3}{2\pi i}\ln 1=\\ -\frac{2{\omega }_3}{2\pi i}2k\pi i=-2k{\omega }_3\end{array}}$

Por lo tanto, un periodo de f(z). Del mismo modo calcularemos

${\displaystyle \frac{1}{2\pi i}{\displaystyle \underset{z_1+2\omega {}_1}{\overset{z_1+2\omega {}_2}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}-\frac{1}{2\pi i}{\displaystyle \underset{z_1}{\overset{z_1+2\omega {}_3}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}.}$

La ecuación del lado de circuito que va de z₁+2ω₁ a z₁+2ω₂ viene dada por:

${\displaystyle z=z_1+2{\omega }_1+(2{\omega }_2-2{\omega }_1)t,0\le t\le 1.}$

Por lo tanto

${\displaystyle \begin{array}{l}\frac{1}{2\pi i}{\displaystyle \underset{z_1+2\omega {}_1}{\overset{z_1+2\omega {}_2}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}=\frac{2{\omega }_3}{2\pi i}{\displaystyle \underset{0}{\overset{1}{\int }}(z_1+2{\omega }_1+2{\omega }_{3}t)\frac{f\text{'}(z_1+2{\omega }_1+2{\omega }_{3}t)}{f(z_1+2{\omega }_1+2{\omega }_{3}t)-A}dt}=\\ =\frac{2{\omega }_3}{2\pi i}{\displaystyle \underset{0}{\overset{1}{\int }}(z_1+2{\omega }_1+2{\omega }_{3}t)\frac{f\text{'}(z_1+2{\omega }_{3}t)}{f(z_1+2{\omega }_{3}t)-A}dt}\end{array}}$

Ahora la ecuación del lado que va de z₁ a z₁+2ω₃ es

${\displaystyle z=z_1+2{\omega }_{3}t,0\le t\le 1.}$

luego

${\displaystyle \frac{1}{2\pi i}{\displaystyle \underset{z_1}{\overset{z_1+2\omega {}_3}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}=\frac{2{\omega }_3}{2\pi i}{\displaystyle \underset{0}{\overset{1}{\int }}(z_1+2{\omega }_{3}t)\frac{f\text{'}(z_1+2{\omega }_{3}t)}{f(z_1+2{\omega }_{3}t)-A}dt}=}$

por tanto

${\displaystyle \begin{array}{l}\frac{1}{2\pi i}{\displaystyle \underset{z_1+2\omega {}_1}{\overset{z_1+2\omega {}_2}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}-\frac{1}{2\pi i}{\displaystyle \underset{z_1}{\overset{z_1+2\omega {}_3}{\int }}z\frac{f\text{'}(z)}{f(z)-A}dz}=\\ \frac{2{\omega }_1}{2\pi i}2{\omega }_3{\displaystyle \underset{0}{\overset{1}{\int }}\frac{f\text{'}(z_1+2{\omega }_{3}t)}{f(z_1+2{\omega }_{3}t)-A}}=\frac{2{\omega }_1}{2\pi i}{\left\{\ln \left[f(z_1+2{\omega }_{3}t)-A\right]\right\}}_0^1=\\ \frac{2{\omega }_1}{2\pi i}\ln \left[\frac{f(z_1+2{\omega }_3)-A}{f(z_1)-A}\right]=\frac{2{\omega }_1}{2\pi i}\ln 1=-\frac{2{\omega }_1}{2\pi i}2m\pi i=2m{\omega }_1\end{array}}$

Como anteriormente un periodo de f(z)

Entonces

${\displaystyle \frac{1}{2\pi i}{\displaystyle \underset{C\text{'}}{\int }z\frac{f\text{'}(z)}{f(z)-A}dz=2m{\omega }_1-2k{\omega }_3=\Omega .}}$

donde Ω será un periodo de la función f(z) con lo cual queda demostrado el teorema.

Teorema 7

La serie

${\displaystyle {\displaystyle \sum \frac{1}{{\left|\Omega \right|}^{\lambda }}}}$ es convergente para λ>2

La sumación se extiende a todos los periodos Ω=2kω₁+2lω₂ excluyendo el valor Ω=0.

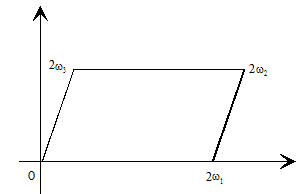
Demostración.- Vemos que todos los periodos Ω distintos de cero están situados en los contornos de ciertos paralelogramos ,semejantes entre sí, con los centros en el origen de coordenadas.
Fijándonos en la figura, el primero de los paralelogramos contiene en su contorno ocho periodos distintos, el segundo dieciséis, el tercero veinticuatro.

Si suponemos, según esto, que el contorno del n-ésimo paralelogramo contiene 8n periodos, entonces, proyectándolos sobre el (n+1)-ésimo paralelogramo en direcciones paralelas a 2ω₁ y 2ω₃, tenemos que a cada periodo situado en el contorno del n-ésimo paralelogramo y distinto de los vértices, le corresponde un periodo en el contorno del (n+1)-ésimo paralelogramo, mientras que a cada uno de los cuatro vértices le corresponden dos periodos; además tenemos que añadir los cuatro vértices del (n+1)-ésimo paralelogramo, con lo cual obtendremos ocho periodos más que en el contorno del n-ésimo paralelogramo, es decir, 8(n+1) periodos.

Como vemos la cantidad de periodos crece en progresión aritmética de razón 8 . Si llamamos d a la distancia del origen de coordenadas hasta el contorno del primer paralelogramo, tendremos que la distancia desde el mismo punto hasta el contorno del n-ésimo paralelogramo es nd.
Entonces, para cualquier periodo Ω situado en el último circuito se cumple

|Ω|≥nd de donde $\frac{1}{{\left|\Omega \right|}^{\lambda }}\le \frac{1}{n^{\lambda }{d}^{\lambda }}$

Por consiguiente

${\displaystyle \begin{array}{l}{\displaystyle \sum \frac{1}{{\left|\Omega \right|}^{\lambda }}}<<\frac{8}{d^{\lambda }}+\frac{2.8}{{(2.d)}^{\lambda }}+\frac{3.8}{{(3.d)}^{\lambda }}+\mathrm{...}+\frac{n.8}{{(n.d)}^{\lambda }}+\mathrm{...}=\\ {\displaystyle \sum _{n=1}^{\infty }\frac{8}{n^{\lambda -1}{d}^{\lambda }}}=\frac{8}{d^{\lambda }}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^{\lambda -1}}}\end{array}}$

que es convergente para λ=3, 4, 5,...

De aquí deducimos que la serie nuestra

${\displaystyle {\displaystyle \sum \frac{1}{{\left|\Omega \right|}^{\lambda }}}}$ también es convergente para λ=3, 4, 5,...

como queríamos demostrar.

Consecuencia.-. La serie

${\displaystyle {\displaystyle \sum \frac{1}{{(z-\Omega )}^3}}}$

es absoluta y uniformemente convergente en cada recinto acotado del plano (donde se quitan una cantidad finita de términos de la serie que tienen polos en este recinto ). Nos es suficiente con suponer que z pertenece a un círculo con centro en el origen de coordenadas |z|<R, y considerar los términos de la serie que corresponden a los periodos Ω que están situados fuera de un círculo de radio 2R.
Entonces, para éstos términos

${\displaystyle \left|\frac{z}{\Omega }\right|<\frac{1}{2}}$ y por tanto,

${\displaystyle \left|\frac{1}{{(z-\Omega )}^3}\right|\le \frac{1}{{(\left|\Omega \right|-\left|z\right|)}^3}=\frac{1}{{\left|\Omega \right|}^3.{\left(1-\frac{\left|z\right|}{\left|\Omega \right|}\right)}^3}<\frac{1}{{\left|\Omega \right|}^3{\left(1-\frac{1}{2}\right)}^3}=\frac{8}{{\left|\Omega \right|}^3}}$

que por el lema anterior es convergente y por tanto la serie

${\displaystyle {\displaystyle \sum \frac{1}{{(z-\Omega )}^3}}}$

es absoluta y uniformemente convergente.

Ahora si designamos a la suma de la serie por g(z), la representaremos en el círculo |z|<R por

${\displaystyle g(z)={\displaystyle \sum _{\left|\Omega \right|\le R}\frac{1}{{(z-\Omega )}^3}}+{\displaystyle \sum _{\left|\Omega \right|>R}\frac{1}{{(z-\Omega )}^3}}}$

Propiedades de la función g(z)

1. La función g(z) es analítica en cualquier círculo |z|<R, a excepción de polos de tercer orden en todos los periodos pertenecientes al círculo indicado. Por lo tanto, es una función meromorfa en todo el plano infinito.

Veamos, la primera suma de la función g(z) es una función racional que tiene un polo de tercer orden en cada periodo perteneciente al círculo |z|<R.

La segunda suma sólo se diferencia en un número finito de términos de la serie

${\displaystyle {\displaystyle \sum _{\left|\Omega \right|>2R}\frac{1}{{(z-\Omega )}^3}}}$

cuya convergencia uniforme en el círculo |z|<R acabamos de ver, por lo tanto es analítica.

2. La función g(z) es periódica siendo 2ω₁, 2ω₃ un par de periodos fundamentales

Primero comprobaremos que 2ω₁ y 2ω₃ son periodos de la función g(z)

${\displaystyle g(z+2{\omega }_j)={\displaystyle \sum \frac{1}{{\left[z-(\Omega -2{\omega }_j)\right]}^3}}}$

Pero Ω-2ω_j también es uno de los periodos dados Ω-2ω_j=Ω₁ y cuando Ω recorre el conjunto de todos los periodos dados, Ω₁ también lo recorre puesto que la transformación Ω-2ω_j=Ω₁ significa un desplazamiento del retículo de periodos según el cual éste se transforma en sí mismo, por tanto la serie

${\displaystyle {\displaystyle \sum \frac{1}{{\left[z-(\Omega -2{\omega }_j)\right]}^3}}}$

sólo se diferencia de la serie

${\displaystyle {\displaystyle \sum \frac{1}{{\left[z-\Omega \right]}^3}}}$

en el orden de sus términos, es decir g(z)=g(z+2ω_j) siendo j = 1, 3.

Ahora veamos que son fundamentales. Para ello, sea ω un periodo cualquiera de la función g(z) como Ω es un polo de g(z) entonces Ω+ω=Ω' tiene que ser uno de los polos, de donde

${\displaystyle \omega =\Omega \text{'}-\Omega =2m_1{\omega }_1+2m_3{\omega }_3}$

Con lo cual, cualquier periodo de la función g(z) se puede poner como combinación lineal de los periodos 2ω₁ y 2ω₃ con coeficientes enteros m₁ y m₃.

3. La función g(z) es elíptica de tercer orden.

Cada vértice del paralelogramo 0, 2ω₁, 2ω₂, 2ω₃, es un polo de tercer orden para g(z), pero de éstos cuatro polos solamente uno, el que está situado en el origen de coordenadas, se incluye en el paralelogramo fundamental, los otros tres pertenecen a los paralelogramos vecinos. Con esto ya tenemos que g(z) es elíptica de tercer orden.



4. La función g(z) es una función impar.

Veamos,

${\displaystyle g(-z)={\displaystyle \sum \frac{1}{{(-z-\Omega )}^3}=-{\displaystyle \sum \frac{1}{{\left[z-(-\Omega )\right]}^3}}}}$

Pero el conjunto de todos los números -Ω coincide con el conjunto de los Ω sí la serie

${\displaystyle {\displaystyle \sum \frac{1}{{\left[z-(-\Omega )\right]}^3}}}$

sólo se diferencia de la serie

${\displaystyle {\displaystyle \sum \frac{1}{{\left[z-\Omega \right]}^3}}}$

en el orden de sus términos, por lo tanto su suma será g(z), y por tanto, g(-z)=-g(z) como queríamos comprobar.

5. Si z_a y z_b son simétricos en un punto (1/2)(m₁2ω₁+m₂2ω₃) con m₁ y m₂ ∈Z y además no congruentes con el cero respecto de los periodos 2ω₁, 2ω₃, entonces

${\displaystyle g(z_a)=-g(z_b)}$

Vamos a comprobarlo,

${\displaystyle \frac{1}{2}(z_a+z_b)=\frac{1}{2}(m_{1}2{\omega }_1+m_{2}2{\omega }_3)\Rightarrow z_a=-z_b+m_{1}2{\omega }_1+m_{2}2{\omega }_3.}$

Luego z_a será congruente con -z_b y por tanto, g(z_a)=g(-z_b) y como la función g(z) es impar obtenemos que

${\displaystyle g(z_a)=-g(z_b)}$

6. La función g(z) tiene ceros en los puntos ω₁, ω₃, (ω₁+ω₃) y todos los puntos congruentes con ellos

Veamos, sean z_a y z_b simétricos en uno de los puntos ω₁, ω₂, (ω₁+ω₃) por la propiedad anterior

${\displaystyle g(z_a)=-g(z_b)}$

Supongamos que z_a y en consecuencia también z_b→ω₁, ω₃ ó (ω₁+ω₃), el que sea, el centro de simetría. Entonces

${\displaystyle g({\omega }_1)=-g({\omega }_1)\Rightarrow 2g({\omega }_1)=0\Rightarrow g({\omega }_1)=0}$

y lo mismo con los otros dos, luego son ceros de la función g(z).

A continuación vamos a integrar la función g(z).

Sea z₁ un punto cualquiera del plano y distinto de los polos de la función g(z). Si integramos término a término la serie

${\displaystyle {\displaystyle \sum \frac{1}{{\left[z-\Omega \right]}^3}}}$

a lo largo de una curva rectificable γ que no pase por los polos y que una a z₁ con otro punto z, también distinto de los polos de la función g(z), obtenemos :

${\displaystyle \phi (z)=C+{\displaystyle \underset{z_1}{\overset{z}{\int }}g(z)dz=C-\frac{1}{2}{\displaystyle \sum \left[\frac{1}{{(z-\Omega )}^2}-\frac{1}{{(z_1-\Omega )}^2}\right]}}.}$

Propiedads de φ(z)

1. La función φ(z) es analítica en z≠Ω

2. La función φ(z) tiene polos de orden dos en cada uno de los puntos Ω y una parte principal.

${\displaystyle -\frac{1}{2{(z-\Omega )}^2}}$

3. La función φ(z) es par.

4. 2ω₁ y 2ω₃ son un par de periodos fundamentales

Escribamos ahora φ(z) en la forma:

${\displaystyle \phi (z)=C-\frac{1}{2}\frac{1}{z^2}+\frac{1}{2}\frac{1}{z_1{}^2}-\frac{1}{2}{\displaystyle \sum _{\Omega \ne 0}\left[\frac{1}{{(z-\Omega )}^2}-\frac{1}{{(z_1-\Omega )}^2}\right]}}$

De esto deducimos que φ(z)+(1/2)z² es una función meromorfa, para la cual el punto z=0 es un punto regular y su valor en dicho punto es:

${\displaystyle {\left[\phi (z)+\frac{1}{2z^2}\right]}_{z=0}=C+\frac{1}{2}\frac{1}{z_1{}^2}-\frac{1}{2}{\displaystyle \sum _{\Omega \ne 0}\left[\frac{1}{{\Omega }^2}-\frac{1}{{(z_1-\Omega )}^2}\right]}}$

Si elegimos la constante de integración C de forma que

${\displaystyle {\left[\phi (z)+\frac{1}{2z^2}\right]}_{z=0}=0}$

Restando término a término las dos expresiones nos resulta,

${\displaystyle \phi (z)=-\frac{1}{2}\left\{\frac{1}{z^2}+{\displaystyle \sum _{\Omega \ne 0}\left[\frac{1}{{(z-\Omega )}^2}-\frac{1}{{\Omega }^2}\right]}\right\}.}$