Cálculos aritméticos

Command Window, es la ventana principal, cuyo propósito es realizar cálculos, correr programas (scripts), asignar valores a variables.
Figure Window, se representan funciones de diversos modos en 2D y en 3D.
Editor Window, crea y depura los ficheros script y función, se obtiene seleccionado en el menú File/New, o en el icono debajo de File
Command History Window, guarda los comandos que se han introducido en Command Window
Workspace Window, proporciona información acerca de las variables que se están utilizando.
Current Folder Window, muestra los ficheros creados y guardados en la carpeta de trabajo
Help Window, proporciona ayuda

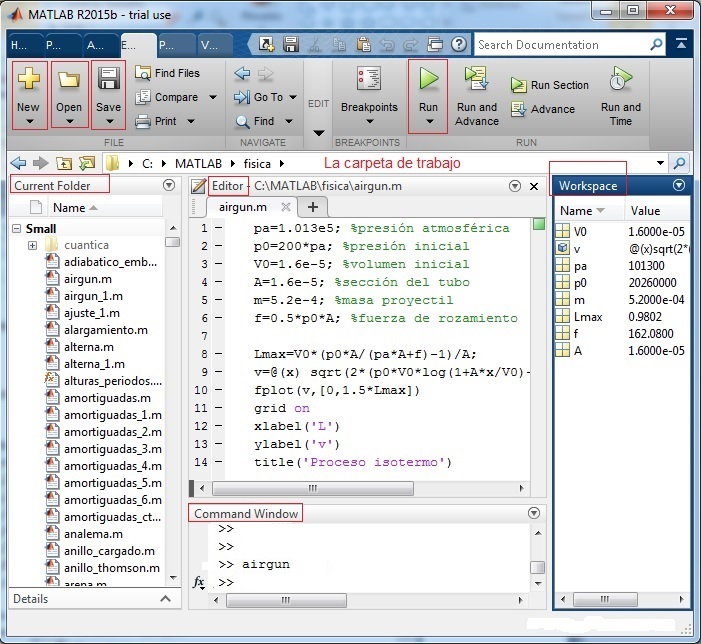
En la figura, se muestra los elementos principales del Entorno de Desarrollo por defecto, seleccionando Layout/Default. En la barra superior, los botones New para crear un script o una función, Open para cargar un script o una función existente en la carpeta de trabajo (un fichero con extensión .m). Save para guardar un script o una función, nuevo o modificado. Run para correr un script como el que aparece en la ventana del editor

Debajo de los botones aparece la ubicación de la carpeta de trabajo, que se selecciona con la flecha hacia abajo al lado de la lupa

Debajo, se disponen cuatro ventanas: la carpeta de trabajo (Current floder) con la lista de los ficheros que podemos ordenar, la ventana del editor (Editor), debajo la ventana de comandos (Command window) y a la derecha la ventana de las variables (Workspace) que han sido creadas cuando corremos el script (Run) con los valores (Value) que guardan

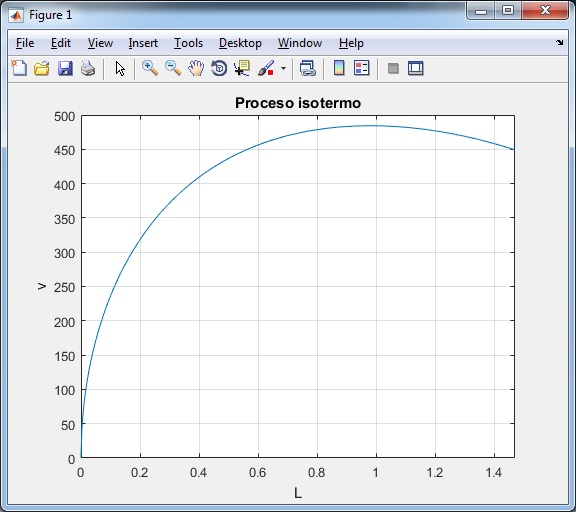
Cuando se ejecuta el script aparece la ventana gráfica Figure 1

Operaciones aritméticas

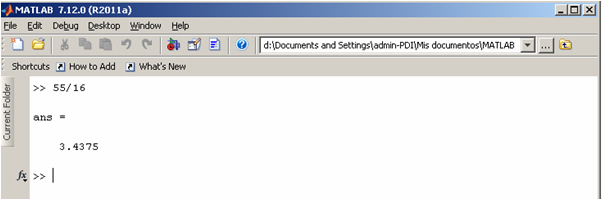
Una vez que se introduce el comando después del símbolo >> y se pulsa la tecla Retorno, el comando se ejecuta

Introducimos 55/16 y pulsamos Retorno

>> 55/16
ans = 3.4375

para calcular el cociente entre 55 y 16, tal como se muestra en la figura

Como ocurre en las calculadoras reutilizamos el último resultado para el siguiente cálculo. Por ejemplo, calculamos el discriminante de una ecuación de segundo grado y lo utilizamos para calcular una de las raíces reales.

MATLAB utiliza la variable ans para guardar el resultado del cálculo. Más adelante veremos el concepto de variable. Sumamos al resultado, 11 y al pulsar Retorno después de 11, obtenemos una nueva respuesta.

>> ans+11
ans = 14.4375

Comentarios

Cuando ponemos el símbolo % al comienzo de la línea, se trata de una línea de comentarios.

>>  %esto es un comentario

Los comentarios vienen precedidos por el carácter % (tanto por ciento) aparecen en color verde en MATLAB y no se procesan. Los comentarios sirven para explicar un comando o una porción de código.

El punto y coma ;

Cuando se pulsa Retorno después del comando se muestra la respuesta del cálculo o del contenido de la variable. Pero si se termina el comando con punto y coma ; y se pulsa Retorno, la respuesta no se muestra.

>> 3*4;

El comando clc

Limpia la ventana de comandos. Este comando no cambia nada, no borra las variables de la memoria

>> clc

Operaciones aritméticas

Suma	+	6+2=8
Diferencia	-	6-2=4
Producto	*	6*2=12
Cociente	/	6/2=3
Elevado a	^	6^2=36

Los comandos nos permiten realizar operaciones aritméticas combinadas como:

>> 5^2+3*4+9/3+8*(5+2)
ans = 96

Paréntesis y precedencia de las operaciones

Las operaciones producto * y el cociente / tienen precedencia sobre la suma + y la diferencia -, tal como podemos ver en el siguiente cuadro. Utilizamos paréntesis para cambiar el orden en el que se efectúan las operaciones

>>  2*3+4
ans = 10
>> 2*(3+4)
ans = 14
>>  2/3+4
ans = 4.6667
>> 2/(3+4)
ans = 0.2857
>> 27^1/3
ans =     9
>> 27^(1/3)
ans =     3

Hay que tener cuidado a la hora de realizar las operaciones, ya que a veces obtenemos un resultado distinto al esperado, si no estamos acostumbrados a escribir las operaciones en una sola línea y no utilizamos de modo adecuado los paréntesis.

Funciones elementales

MATLAB dispone de numerosas funciones predefinidas, algunas de ellas son las siguientes:

abs(x)	Valor absoluto de x
sqrt(x)	Raíz cuadrada de x
nthroot(x,n)	Raíz n de x. Si n=3 sería la raíz cúbica de x
sign(x)	Devuelve -1 si x es menor que 0, 0 si x es igual a 0, y 1 en el otro caso
rem(x,y)	Devuelve el resto de la división x/y . Por ejemplo, rem(26,4) devuelve 2
exp(x)	Calcula e^x
log(x)	Calcula lnx, logaritmo natural
log10(x)	Calcula log₁₀x, logaritmo en base 10 de x
sin(x) sind(x)	Calcula el seno de x, x en radianes (o grados)
cos(x) cosd(x)	Calcula el coseno de x, x en radianes (o grados)
tan(x) tand(x)	Calcula la tangente de x, x en radianes (o grados)
asin(x) asind(x)	Calcula el arco seno, donde x ha de ser un número comprendido entre -1 a 1. La función devuelve el ángulo en radianes entre -π/2 y +π/2 (o grados)
acos(x) acosd(x)	Calcula el arco coseno, donde x ha de ser un número comprendido entre -1 a 1. La función devuelve el ángulo en radianes entre 0 y π (o grados)
atan(x) atand(x)	Calcula el arco tangente. La función devuelve el ángulo en radianes entre -π/2 y +π/2 (o grados)
atan2(y,x)	Calcula el arco tangente de y/x. Devuelve el ángulo en radianes entre -π y +π, dependiendo del signo de x e y
sinh(x)	Calcula $\frac{e^{x} - e^{- x}}{2}$
cosh(x)	Calcula $\frac{e^{x} + e^{- x}}{2}$
tanh(x)	Calcula $\frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}$
asinh(x)	Calcula $\ln (x + \sqrt{x^{2} + 1})$ (*)
acosh(x)	Calcula $\ln (x + \sqrt{x^{2} - 1})$ (*)
atanh(x)	Calcula $\ln \sqrt{\frac{1 + x}{1 - x}} para \| x \| \leq 1$ (*)
factorial(x)	Calcula 1·2·3···x

(*) Al final de la página, se justifican las fórmulas correspondientes a asinh, acosh y atanh

Para calcular la raíz cuadrada de un número positivo $\sqrt{144}$ , escribimos

>> sqrt(144)
ans = 12

La raíz cuadrada de un número negativo $\sqrt{-4}$ , escribimos

>> sqrt(-4)
ans = 0 + 2.0000i

nos da un número complejo

Calculamos la raíz cuarta de un número positivo, $\sqrt[4]{6561}$

>> nthroot(6561,4)
ans = 9

No se puede calcular la raíz cuarta de un número negativo, Se puede calcular la raíz n de un número negativo si el resultado es real, es decir, si n es impar.

Para calcular el seno de 30 grados se escribe

>> sind(30)
ans = 0.5000

Los ángulos se expresan también en radianes. Para calcular el seno de 30°=π/6 se escribe

>> sin(pi/6)
ans = 0.5000

El ángulo cuyo coseno es -0.5 se calcula del siguiente modo

>> acos(-0.5)
ans = 2.0944  (respuesta en radianes)

O bien,

>> acosd(-0.5)
ans = 120  (respuesta en grados)

Resto de la división entre dos números x e y: 14=4×3+2

>> rem(14,4)
ans = 2

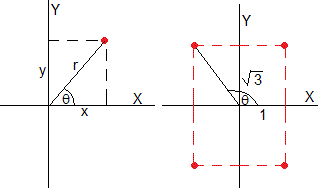
La transformación entre coordendas rectangulares y polares es una operación frecuente en Física

$\begin{array}{l} r = \sqrt{x^{2} + y^{2}} \\ \tan θ = \frac{y}{x} \end{array}$

La función atn nos da los mismos valores del ángulo θ para el primer y tercer cuadrante, para el segundo y cuarto

>> atan(sqrt(3))*180/pi
ans =   60.0000
>> atan(-sqrt(3))*180/pi
ans =  -60.0000

que tendremos que discriminar dependiendo del signo de la abscisa x. Es más apropiado, utilizar la función atan2 para esta tarea

>> atan2(sqrt(3),1)*180/pi
ans =   60.0000
>> atan2(sqrt(3),-1)*180/pi
ans =  120.0000
>> atan2(-sqrt(3),-1)*180/pi
ans = -120.0000
>> atan2(-sqrt(3),1)*180/pi
ans =  -60.0000

Para el tercer y cuarto cuadrante atan2 produce ángulos negativos, que se convierten en positivos sumando 360°

Formatos

Representación de los números en MATLAB

Número	Mantisa-exponente	MATLAB
2412.6	2.4126×10³	2.4126e3
0.00002	2×10^-5	2e-5
20000	2×10⁴	2e4

Podemos representar un número como 0.00002 o bien, 2e-5

Si queremos mostrar un resultado con muchos decimales, escribimos

>> format long
>> pi
ans = 3.141592653589793

Si queremos mostrar menos decimales

>> format short
>> pi
ans =  3.1416

format short	4 decimales si 0.001≤numero≤1000 de otro modo, el formato es short e	>> 351/7 ans=50.1429 >> 35100/7 ans = 5.0143e+03
format long	15 decimales, si 0.001≤numero≤100 de otro modo, el formato es long e	>> 351/7 ans = 50.142857142857146 >> 3510/7 ans = 5.014285714285714e+02
format short e	Notación científica con 4 decimales	>> 351/7 ans = 5.0143e+001
format long e	Notación científica con 14 decimales	>> 351/7 ans = 5.014285714285715e+001
format short g	Notación científica con 5 decimales	>> 351/7 ans = 50.143
format long g	Notación científica con 15 decimales	>> 351/7 ans = 50.1428571428571
format bank	2 decimales	>> 351/7 ans = 50.14

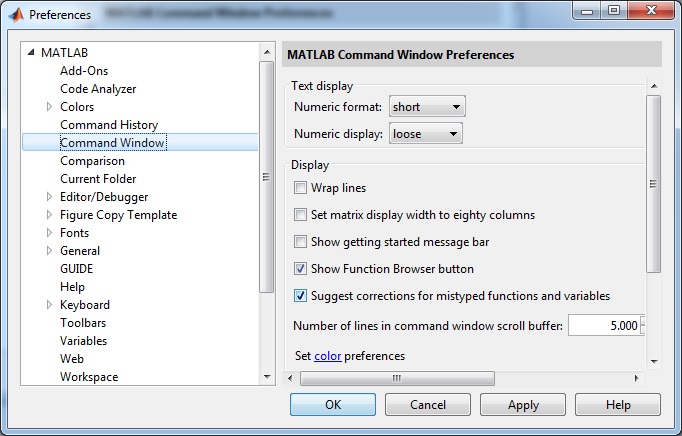
El formato por defecto (short) y otras características del entorno MATLAB se pueden cambiar en el cuadro de diálogo titulado MATLAB Command Window Preferences

Fracciones

Podemos operar con fracciones y obtener el resultado de la operación como una fracción simplificada, estableciendo el formato rational o rat

>>  format rat
>>  12/18
ans  = 2/3
>>  1/2+2/3
ans  = 7/6
>>  1/2*2/3
ans  = 1/3
>>  (2/3)/(4/5)
ans  = 5/6

Volvemos al formato por defecto

>> format short

Aproximación a números enteros

La función round aproxima un número decimal al entero más próximo.

>> round(2.52)
ans =     3
>> round(2.49)
ans =     2
>> round(2.5)
ans =     3

La función ceil redondea hacia arriba, la función floor redondea hacia abajo

>> floor(2.51)
ans =     2
>> ceil(2.4)
ans =     3

La función fix elimina la parte decimal

>> fix(2.49)
ans =     2
>> fix(-2.4)
ans =    -2

Ayuda

Obtenemos información acerca de una palabra reservada por MATLAB (comando, función, etc) mediante help seguido de dicha palabra. Por ejemplo, queremos tener información sobre la función que calcula el seno (sin) de un ángulo.

>> help sin
SIN    Sine of argument in radians.
SIN(X) is the sine of the elements of X.
 
See also asin, sind.

    Reference page for sin
    Other functions named sin

MATLAB, como herramienta de cálculo

MATLAB es una buena herramienta para realizar los cálculos que solemos hacer con una calculadora científica, pero hace mucho más como vamos a ver a lo largo de estas páginas.

Nota, funciones: asinh, acosh, atanh

y=asinh(x)

$\begin{array}{l} \sinh (x) = \frac{e^{x} - e^{- x}}{2} = y \\ e^{2 x} - 1 = 2 y e^{x} \\ e^{2 x} - 2 y e^{x} - 1 = 0 \\ e^{x} = \frac{2 y + \sqrt{4 y^{2} + 4}}{2} \\ x = \ln (y + \sqrt{y^{2} + 1}) \end{array}$

y=acosh(x)

$\begin{array}{l} \cosh (x) = \frac{e^{x} + e^{- x}}{2} = y \\ e^{2 x} + 1 = 2 y e^{x} \\ e^{2 x} - 2 y e^{x} + 1 = 0 \\ e^{x} = \frac{2 y + \sqrt{4 y^{2} - 4}}{2} \\ x = \ln (y + \sqrt{y^{2} - 1}) \end{array}$

y=atanh(x)

$\begin{array}{l} \tanh (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}} = y \\ e^{2 x} (1 - y) = 1 + y \\ e^{x} = \sqrt{\frac{1 + y}{1 - y}} \\ x = \ln \sqrt{\frac{1 + y}{1 - y}} \end{array}$

con |y|<1