Ejemplos
Sistema de ecuaciones lineales. Regla de Cramer
Sea un sistema lineal de tres ecuaciones con tres incógnitas. Aplicamos la regla de Cramer
A·X=B. Donde A es la matriz de los coeficientes, B es el vector de los términos independientes y X es el vector de las incógnitas.
Vamos a elaborar un script para resolver un sistema de ecuaciones lineales que es compatible y determinado y lo aplicaremos al siguiente ejemplo.
A=[0,4,-2,-2;1,2,4,-3;-3,-3,8,-2;-1,1,6,-3];
B=[-4,5,7,7]'; %vector columna
den=det(A); %denominador
X=zeros(length(B),1); %vector columna
for j=1:length(B)
num=A;
num(1:end,j)=B; %matriz numerador
X(j)=det(num)/den; %incógnitas
end
disp(X) %incógnitas
disp(A*X) %comprobación
Determinamos el vector de las incógnitas y comprobamos que el producto A·X es el vector B de los términos independientes
0.6000 %incógnitas
1.6000
2.4000
2.8000
-4.0000 %comprobación
5.0000
7.0000
7.0000
Rellenar un área de color
Utilizamos los vectores en combinación con los operadores lógicos para producir ciertos efectos que nos pueden ser útiles en las representaciones gráficas.
El comando
Primero, vamos a recordar como se extrae un vector de otro mediante operadores lógicos
>> x=linspace(-1.5,4.5,10) x =-1.5000 -0.8333 -0.1667 0.5000 1.1667 1.8333 2.5000 3.1667 3.8333 4.5000 >> u=x>1 & x<3 u = 0 0 0 0 1 1 1 0 0 0 >> x(u) ans = 1.1667 1.8333 2.5000
Como vemos, se extraen aquellos elementos cuyo índice se corresponde con el valor uno.
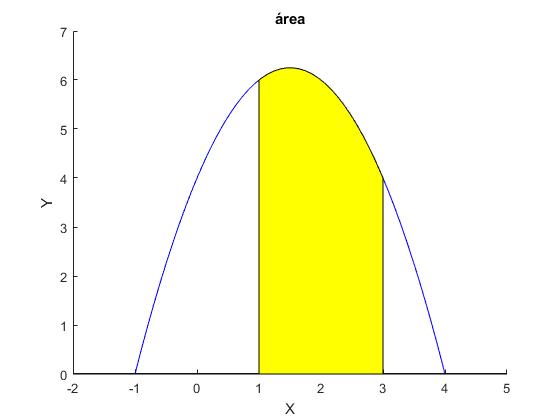
Dibujamos la función -x2+3x+4 y definimos la región comprendida entre la curva, el eje X y las rectas x=1 y x=3 que queremos colorear con el comando
Punto
x=linspace(-1,4,50);
f=@(x) -x.^2+3*x+4;
y=f(x);
hold on
plot(x,y,'b')
line([-2 5],[0 0],'color','k'); %eje horizontal X
xx=[1 1 x(x>1 & x<3) 3 3];
yy=[0 f(1) y(x>1 & x<3) f(3) 0];
fill(xx,yy,'y'); %rellena un área de color especificado
title('área')
xlabel('X')
ylabel('Y')
hold off
Máximos de una función
Representamos la función suma de cuatro armónicos de frecuencias angulares ω=1, 3, 3.5, 4 y 6 rad/s en el intervalo (0.1,10)
x(t)=cos(t)+0.5·cos(3t)+0.4·cos(3.5t)+0.7·cos(4t)+0.2·cos(6t)
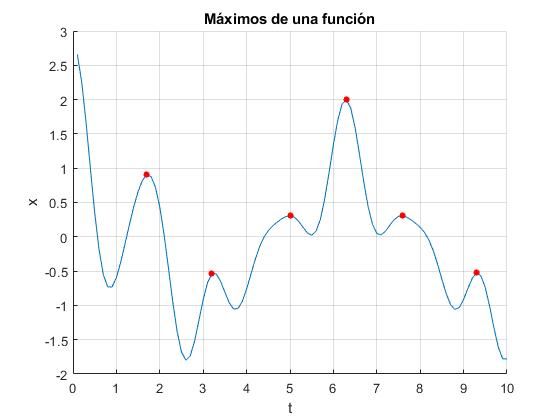
Nos fijamos en el primer máximo que está en el intervalo (1,2). La función crece hasta
>> s=[1,2,5]; >> diff(s) ans = 1 3
dx(dx<=0)=-1 |
|||||
|---|---|---|---|---|---|
| 10 | 1.0 | -0.5948 | 0.2258 | 1 | 0 |
| 11 | 1.1 | -0.3690 | 0.2698 | 1 | 0 |
| 12 | 1.2 | -0.0992 | 0.2778 | 1 | 0 |
| 13 | 1.3 | 0.1786 | 0.2599 | 1 | 0 |
| 14 | 1.4 | 0.4385 | 0.2216 | 1 | 0 |
| 15 | 1.5 | 0.6601 | 0.1630 | 1 | 0 |
| 16 | 1.6 | 0.8231 | 0.0808 | 1 | -2 |
| 17 | 1.7 | 0.9039 | -0.0268 | -1 | 0 |
| 18 | 1.8 | 0.8771 | -0.1550 | -1 | 0 |
| 19 | 1.9 | 0.7220 | -0.2896 | -1 | 0 |
| 20 | 2.0 | 0.4324 | -0.4078 | -1 | 0 |
El primer máximo corresponde al índice
En la tabla la variable
>> s=[0,0,2,0,0,0,0]; >> find(s>0) ans = 3
El código para identificar los máximos de una función es el siguiente
t=0.1:0.1:10;
x=cos(t)+0.5*cos(3*t)+0.4*cos(3.5*t)+0.7*cos(4*t)+0.2*cos(6*t);
hold on
plot(t,x)
dx=diff(x);
dx(dx>0)=1;
dx(dx<=0)=-1;
d2x=diff(dx);
indice_max=find(d2x<0)+1; %<0, máximos; >0 mínimos
t_max=t(indice_max);
for i=1:length(indice_max)
plot(t_max(i),x(indice_max(i)),'ro','markersize',4,'markerfacecolor','r')
end
hold off
grid on
xlabel('t')
ylabel('x')
title('Máximos de una función')
Cálculo de impuestos
La fórmula para calcular los impuestos de los salarios brutos de los empleados de una hopotética empresa es la siguiente:
| Salario bruto | Impuestos |
|---|---|
| Menos de 1000 € | 5% del salario bruto |
| Entre 1000 y 2500 € | 50 € más el 15% de la diferencia entre el salario y 1000 € |
| Entre 2500 y 4000 € | 275 € más el 30% de la diferencia entre el salario y 2500 € |
| Más de 4000 € | 725 € más el 40% de la de la diferencia entre el salario y 4000 € |
Calcular e imprimir en una tabla el salario real de los empleados cuyo salario bruto es: 800, 2300, 3000, 3800 y 4200.
sb=[800 2300 3000 3800 4200]; %salario bruto
for k=sb
if k<1000
descuento=0.05*k;
elseif k<2500
descuento=50+0.15*(k-1000);
elseif k<4000
descuento=275+0.3*(k-2500);
else
descuento=725+0.4*(k-4000);
end
disp([k k-descuento])
end
Corremos el script en la ventana de comandos
>> salario
800 760
2300 2055
3000 2575
3800 3135
4200 3395
Escribimos este script de forma alternativa, sin necesidad de sentencias condicionales (
sb=[800 2300 3000 3800 4200]; %salario bruto
descuento=(sb<1000).*sb*0.05+...
(sb>=1000 & sb<2500).*(50+(sb-1000)*0.15)+...
(sb>=2500 & sb<4000).*(275+(sb-2500)*0.3)+...
(sb>=4000).*(725+(sb-4000)*0.4);
disp([sb' (sb-descuento)'])
Como podemos apreciar cada línea que calcula el vector
| 800 | 2300 | 3000 | 3800 | 4200 | |
|---|---|---|---|---|---|
| |
1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 1 | 0 | |
| 0 | 0 | 0 | 0 | 1 |
Ahora veamos el producto elemento a elemento de los vectores
>> (sb<1000).*sb ans = 800 0 0 0 0
multiplicando el vector [800,0,0,0,0] por 0.05 obtenemos el vector [40,0,0,0,0] que corresponde al descuento para los salarios brutos menores de 1000 euros. Del mismo modo, podemos probar la siguiente línea que calcula el descuento de los salarios comprendidos entre 1000 y 2500 euros. El salario bruto en este intervalo es 2300 euros, por tanto su descuento es 50+(2300-1000)*0.15=245.
Los vectores de la izquierda y de la derecha son, respectivamente
>> (sb>=1000 & sb<2500) ans = 0 1 0 0 0 >> (50+(sb-1000)*0.15) ans = 20 245 350 470 530
El producto elemento a elemento de ambos vectores es [0,245,0,0,0] que corresponde al descuento del segundo salario bruto. Así, para cada vector de salarios brutos sb obtenemos el correspondiente vector de descuentos debidos a los impuestos.
Al correr el script obtenemos una tabla cuya primera columna son los salarios brutos y la segunda los mismos con la deducción por impuestos
800 760
2300 2055
3000 2575
3800 3135
4200 3395
Binomio de Newton
Definimos una función denominada
Primero calculamos el número combinatorio nCm o n sobre m.
Definimos la función
function r=combinatorio(n,m)
k=1:m;
t=(n-k+1)./k;
r=prod(t);
end
Alternativamente, podemos utilizar la función de MATLAB
>> combinatorio(4,2) ans = 6 >> nchoosek(4,2) ans = 6
Definimos la función
function p=pol_newton(n,a)
p=zeros(1, n+1); %reserva espacio en memoria e inicializa a cero
for k=0:n
p(k+1)=combinatorio(n,k)*a^k;
end
end
Probamos la función
>>pol_newton(2,1) ans = 1 2 1 >> pol_newton(3,1) ans = 1 3 3 1 >> pol_newton(4,1) ans = 1 4 6 4 1 >> pol_newton(3,-1) ans = 1 -3 3 -1
Sumas y productos
Dado un conjunto de datos x1,x2....xn, calcular la suma de los siguientes productos
s=(x1-x2)·(x1-x3)...(x1-xn)+(x2-x1)·(x2-x3)...·(x2-xn)+....+(xn-x1)·(xn-x2)...·(xn-xn-1)
En el capítulo Vectores aprendimos a extraer elementos de un vector con otro vector
>> x=[0.97 1.12 2.92 3.00]; >> indice=[1 3 4]; >> x(indice) ans = 0.9700 2.9200 3.0000
Vemos se obtiene el vector
Cuando
>> x=[0.97 1.12 2.92 3.00 3.33 3.97 6.10 8.39 8.56 9.44]; >> n=length(x); >> k=3; >> indice=[1:k-1 k+1:n] indice = 1 2 4 5 6 7 8 9 10 >> x(indice) ans = 0.9700 1.1200 3.0000 3.3300 3.9700 6.1000 8.3900 8.5600 9.4400 >> k=1; >> indice=[1:k-1 k+1:10] indice = 2 3 4 5 6 7 8 9 10 >> x(indice) ans = 1.1200 2.9200 3.0000 3.3300 3.9700 6.1000 8.3900 8.5600 9.4400
Ahora, podemos codificar fácilmente el resultado de la suma de los productos anteriores, recordando que la función
x=[0.97 1.12 2.92 3.00 3.33 3.97 6.10 8.39 8.56 9.44];
suma=0;
n=length(x);
for i=1:n
suma=suma+prod(x(i)-x([1:i-1 i+1:n]));
end
fprintf('La suma es %2.3f\n ',suma)
Corremos el script en la ventana de comandos
>> prueba La suma es 274113.275
Posición del asteriode Pallas
Gauss estaba interesado en calcular de un modo preciso la órbita del asteroide Pallas, a partir de las observaciones de su posición.
| Ascensión | 0 | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 | 330 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Declinación | 408 | 89 | -66 | 10 | 338 | 807 | 1238 | 1511 | 1583 | 1462 | 1183 | 804 |
Disponía de 12 pares de datos (ti,xi) que deseaba interpolar con la suma de seis funciones armónicas.
x= A0+A1cos(ωt)+ B1sin(ωt)+ A2cos(2ωt)+ B2sin(2ωt)+...+ Amcos(mωt)+ Bmsin(mωt)
Donde los coeficientes A0, A1...Am, B1...Bm valen, véase al final de la página Ajuste de datos con funciones armónicas.
En primer lugar, representamos los datos
t=0:30:330;
x=[408 89 -66 10 338 807 1238 1511 1583 1462 1183 804];
hold on
plot(t,x,'ro','markersize',2,'markerfacecolor','r')
xlim([0 360])
xlabel('Ascensión (Grados)')
ylabel('Declinación (Minutos)')
title('Posición del asteroide Pallas')
grid on
Calculamos ahora los coeficientes A0, A1...A6, B1...B6 mediante las expresiones anteriores. La primera intención es utilizar un doble bucle: uno para obtener las sumas parciales y otro para obtener cada uno de los seis coeficientes a y b.
n=length(x);
w=2*pi/360;
a0=sum(x)/n;
a=zeros(1,6); %reserva espacio en memoria para seis elementos
b=zeros(1,6);
for k=1:6
for i=1:n
a(k)=a(k)+x(i)*cos(k*w*t(i))*2/n;
b(k)=b(k)+x(i)*sin(k*w*t(i))*2/n;
end
end
Si tenemos en cuenta como se realizan las operaciones con matrices, podemos reducir significativamente las líneas de código marcadas en negrita:
- El producto de dos matrices de dimensiones (m×k)×(k×n)=(m×n) es una matriz de dimensión m×n
- El producto de un escalar por una matriz es otra matriz de la misma dimensión, cuyos elementos han sido multiplicados por el escalar.
- El coseno o el seno de una matriz, por ejemplo cos(A) es la matriz B(i,j)=cos(A(i,j)), se calcula el coseno de cada uno de los elementos de la matriz, obteniéndose otra matriz de la misma dimensión.
k=1:6; a=cos(w*k'*t)*x'*2/n b=sin(w*k'*t)*x'*2/n
Al correr el script, obtenemos dos vectores columna
a =
-411.0144
43.4167
-4.3333
-1.0833
0.3477
0.1667
b =
-720.2279
-2.1651
5.5000
-1.0104
-0.2721
-0.0000
Conocidos los coeficientes A0, A1...A6, B1...B6, representamos la función x(t), junto a las medidas (ti,xi) en la misma ventana gráfica (hold on)
x= A0+A1cos(ωt)+ B1sin(ωt)+ A2cos(2ωt)+ B2sin(2ωt)+...+ A6cos(6ωt)+ B6sin(6ωt)
t=0:360; x=a0+a'*cos(w*k'*t)+b'*sin(w*k'*t); plot(t,x,'b') hold off
Ahora
Unimos las porciones de código en un único script
t=0:30:330;
x=[408 89 -66 10 338 807 1238 1511 1583 1462 1183 804];
hold on
plot(t,x,'ro','markersize',4,'markerfacecolor','r')
n=length(x);
w=2*pi/360;
a0=sum(x)/n;
k=1:6;
a=cos(w*k'*t)*x'*2/n;
b=sin(w*k'*t)*x'*2/n;
t=0:360;
x=a0+a'*cos(w*k'*t)+b'*sin(w*k'*t);
plot(t,x,'b')
xlim([0 360])
xlabel('Ascensión (grados)')
ylabel('Declinación (minutos)')
title('Posición del asteroide Pallas')
grid on
hold offf
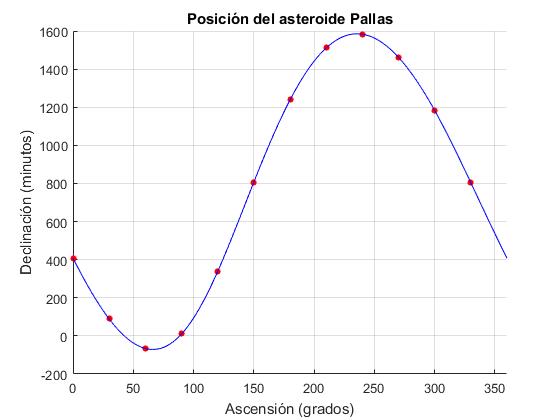
Ejemplos del curso de Física
Funciones básicas: sqrt, sin, etc. y programación
Dinámica de una partícula unida a una goma elástica
Secuencia de colisiones elásticas (II)
Trayectoria de un proyectil disparado desde la superficie de la Tierra
Trayectoria de un proyectil disparado desde una altura h sobre la superficie de la Tierra
Desviación hacia el este de un cuerpo que cae
Choque de un meteorito con la Tierra
Encuentro de una sonda espacial con el planeta Júpiter
Macroestado, microestados. Temperatura, entropía
Vaciado de un depósito cerrado
Esfera cargada próxima a un plano conductor a potencial cero
Dos esferas conductoras una de las cuales está a potencial cero
Fuerza entre dos esferas conductoras
Circuitos de corriente alterna
Intensidad de la radiación solar sobre una superficie plana inclinada
Producto escalar: dot, norm
Suma de los términos de una serie: sum
Sucesivos rebotes en un plano inclinado
Formulación discreta de las ecuaciones del movimiento de un cohete
Análisis de las alturas y periodos de las olas

