Números complejos

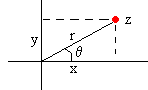
Un número complejo se escribe z=x+iy. x es la parte real, y es la parte imaginaria. $i = \sqrt{- 1}$ es la unidad imaginaria

Forma polar de un número complejo

$\begin{array}{l} z = x + i y \\ {\begin{cases} x = r \cdot \cos θ \\ y = r \cdot \sin θ \end{cases} {\begin{cases} r = \sqrt{x^{2} + y^{2}} \\ \tan θ = \frac{y}{x} \end{cases} \\ z = r \cdot \cos θ + i r \cdot \sin θ = r (\cos θ + i \sin θ) = r e^{i θ} \end{array}$

>> 3+i*4
ans = 3.0000+4.0000i 
>> complex(1,2)
ans =   1.0000 + 2.0000i
>> z=2*exp(i*pi/6)
z =   1.7321 + 1.0000i 
>> z1=2*cos(pi/6)+i*2*sin(pi/6)
z1 =   1.7321 + 1.0000i

Son idénticos los números complejos

$\begin{array}{l} z_{1} = r \exp (i θ) \\ z_{2} = r \exp (i (θ + 2 k π)) k = 0, \pm 1, \pm 2, \pm 3... \end{array}$

Las funciones MATLAB que se aplican a estos números son:

abs(z)	Módulo del número complejo z
angle(z)	Argumento (en radianes) del número complejo z. El ángulo está comprendido entre -π y +π
conj(z)	Número complejo conjugado de z
real(z)	Devuelve la parte real del número complejo z
imag(z)	Devuelve la parte imaginaria del número complejo z

$\begin{array}{l} z = x + i y \\ | z | = \sqrt{x^{2} + y^{2}} \\ θ = {\begin{cases} \tan^{- 1} (\frac{y}{x}) x > 0 y > 0 \\ π - \tan^{- 1} (\frac{y}{| x |}) x < 0 y > 0 \\ - (π - \tan^{- 1} (\frac{| y |}{| x |})) x < 0 y < 0 \\ - \tan^{- 1} (\frac{| y |}{x}) x > 0 y < 0 \end{cases} \end{array}$

Expresamos un número complejo en forma polar

>> abs(4+i*3)
ans = 5
>> angle(4+i*3)
ans = 0.6435
>> 5*exp(i*0.6435)
ans =   4.0000 + 3.0000i
>> angle(4-i*3)*180/pi
ans = -36.8699
>> angle(-4-i*3)*180/pi+360
ans = 216.8699

MATLAB expresa los ángulos en el intervalo (-π, π) o bien (-180, 180) Si el ángulo es negativo le sumamos 2π ó 360 para que se exprese en el intervalo (0, 2π), o bien (0,360)

Operaciones con números complejos

Podemos hacer operaciones con números complejos, tales como suma, diferencia, producto, cociente, potencia y raíz

$\begin{array}{l} z_{1} = x_{1} + i y_{1} = r_{1} \exp (i θ_{1}) \\ z_{2} = x_{2} + i y_{2} = r_{2} \exp (i θ_{2}) \\ z_{1} + z_{2} = (x_{1} + x_{2}) + i (y_{1} + y_{2}) \\ z_{1} - z_{2} = (x_{1} - x_{2}) + i (y_{1} - y_{2}) \\ z_{1} \cdot z_{2} = r_{1} r_{2} \exp i (θ_{1} + θ_{2}) \\ z_{1} \cdot z_{2} = (x_{1} x_{2} - y_{1} y_{2}) + i (x_{1} y_{2} + x_{2} y_{1}) \\ \frac{z_{1}}{z_{2}} = \frac{r_{1}}{r_{2}} \exp i (θ_{1} - θ_{2}) \\ \frac{z_{1}}{z_{2}} = \frac{(x_{1} x_{2} + y_{1} y_{2}) + i (x_{2} y_{1} - x_{1} y_{2})}{x_{2}^{2} + y_{2}^{2}} \end{array}$

>> (2+i*5)+(3-i*2)
ans = 5.0000 +  3.0000i
>> (2+i*5)*(3-i*2)
ans = 16.0000 +11.0000i
>>  (2+i*5)/(3-i*2)
ans  = -0.3077 + 1.4615i

Comprobamos el producto de dos números complejos en forma polar

>> z1=2*exp(i*pi/6)
z1 =   1.7321 + 1.0000i
>> z2=3*exp(i*pi/4)
z2 =   2.1213 + 2.1213i
>> z=z1*z2
z =   1.5529 + 5.7956i
>> abs(z)
ans =    6.0000
>> angle(z)
ans =    1.3090
>> pi/6+pi/4
ans =    1.3090

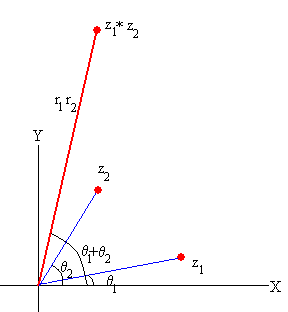
La multiplicación de los números complejos

z₁=r·exp(iθ₁) y z₂=exp(iθ₂)
z=z₁·z₂=r·exp(i(θ₁+ θ₂))

equivale a la rotación de z₁ un ángulo θ₂.

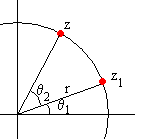
La fórmula de Moivre es una interesante aplicación de la forma polar de un número complejo

$\begin{array}{l} {(e^{i θ})}^{n} = e^{i n θ} \\ {(\cos θ + i \sin θ)}^{n} = \cos (n θ) + i \sin (n θ) \end{array}$

La potencia n de un número complejo z se calcula por la fórmula de Moivre del siguiente modo

$z^{n} = r^{n} (\cos (n θ) + i \sin (n θ))$

El producto de números complejos nos conduce a la fórmula del coseno de la suma de dos ángulo y la del seno de la suma de dos ángulo

$\begin{array}{l} z_{1} \cdot z_{2} = r_{1} (\cos θ_{1} + i \sin θ_{1}) r_{2} (\cos θ_{2} + i \sin θ_{2}) = \\ r_{1} r_{2} ((\cos θ_{1} \cos θ_{2} - \sin θ_{1} \sin θ_{2}) + i (\cos θ_{1} \sin θ_{2} + \sin θ_{1} \cos θ_{2})) \\ z_{1} \cdot z_{2} = r_{1} r_{2} \exp (i (θ_{1} + θ_{2})) = r_{1} r_{2} (\cos (θ_{1} + θ_{2}) + i \sin (θ_{1} + θ_{2})) \\ {\begin{cases} \cos (θ_{1} + θ_{2}) = \cos θ_{1} \cos θ_{2} - \sin θ_{1} \sin θ_{2} \\ \sin (θ_{1} + θ_{2}) = \cos θ_{1} \sin θ_{2} + \sin θ_{1} \cos θ_{2} \end{cases} \end{array}$

Complejo conjugado

Para cada número complejo z=x+iy=r·exp(iθ), existe un número complejo conjugado

$\begin{array}{l} z = x + i y = r \exp (i θ) \\ \bar{z} = x - i y = r \exp (- i θ) \\ z \cdot \bar{z} = (x + i y) \cdot (x - i y) = x^{2} + y^{2} \\ z \cdot \bar{z} = r \exp (i θ) * r \exp (- i θ) = r^{2} \end{array}$

El producto de un número complejo por su correspondiente conjugado nos da el cuadrado del módulo

>> z=3+4*i;
>> abs(z)
ans =     5
>> z1=conj(z)
z1 =   3.0000 - 4.0000i
>> z*z1
ans =    25

Parte real Re(z) e imaginaria Im(z) de un número complejo z=x+iy es devuelto por las funciones real(z) e imag(z)

>> real(3+4i)
ans =     3
>> imag(3+4i)
ans =     4

Otra forma alternativa de calcular la parte real e imaginaria de un número compejo es

$Re (z) = \frac{z + \bar{z}}{2} Im (z) = \frac{z - \bar{z}}{2 i}$

Raíces de un número complejo

La raíz n de un número complejo z es

$\sqrt[k]{z} = \sqrt[n]{r} \exp (i \frac{θ + 2 π k}{n}) k = 0... n - 1$

Para calcular la raíz cúbica del número complejo z=3+4i, escribimos

>> z=3+4*i;
>> n=3;
>> k=0:n-1;
>> z1=nthroot(abs(z),n)*exp(i*(angle(z)+2*pi*k)/n)
>> compass(z1)
z1 =   1.6289 + 0.5202i  -1.2650 + 1.1506i  -0.3640 - 1.6708i

El comando compass nos permite representar gráficamente un número complejo o un vector de números complejos en el plano.

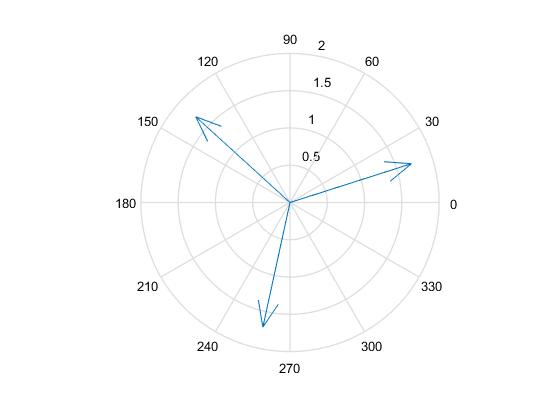
Las raíces de la ecuación z⁸=1 son

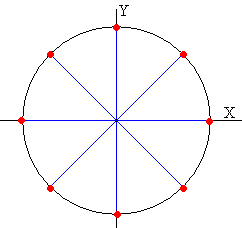
$\begin{array}{l} z_{k} = \exp (i \frac{2 π k}{8}) = \cos \frac{2 π k}{8} + i \sin \frac{2 π k}{8}, k = 0,1,2...7 \\ \pm 1, \pm i, \pm (1 + i) \frac{\sqrt{2}}{2}, \pm (1 - i) \frac{\sqrt{2}}{2} \end{array}$

Las raíces de la ecuación zⁿ=c, se sitúan en un círculo y forman los vértices de un polígono regular de n lados.

Creamos un script para determinar las raíces de un número complejo

z=input('Número complejo: ');
N=input('Raíz: ');
n=0:N-1;
z1=nthroot(abs(z),N)*exp(i*(angle(z)+2*pi*n)/N)
compass(z1)

Propiedades geométricas

Distancia entre dos puntos del plano

$| z_{1} - z_{2} | = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$

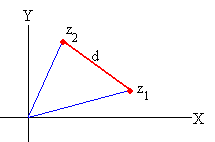
Desigualdad entre los lados de un triángulo

$| z_{1} + z_{2} | \leq | z_{1} | + | z_{2} |$

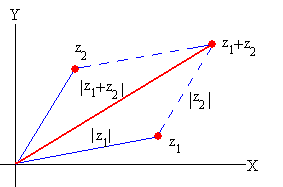
Comprobar esta desigualdad para z₁=7+i y z₂=3+5i

>> z1=7+i;
>> z2=3+5*i;
>> d=abs(z1-z2)
d =    5.6569
>> s=abs(z1+z2)
s =   11.6619
>> d1=abs(z1)
d1 =    7.0711
>> d2=abs(z2)
d2 =    5.8310
>> s<d1+d2 %es |z1+z2|≤|z1|+|z2|
ans =     1 %verdadero