Sentencias condicionales

if

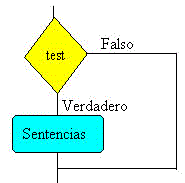
La sentencia if, actúa como cabría esperar. Si la condición es verdadera, la sentencia se ejecuta, de otro modo, se salta dicha sentencia, continuando la ejecución del programa con otras sentencias a continuación de ésta. La forma general de la sentencia if es:

Ejemplos

if a < b
if a >= 3
if b ~= 0
if (x>=2) & (x<10)

if condicion
    sentencias
end

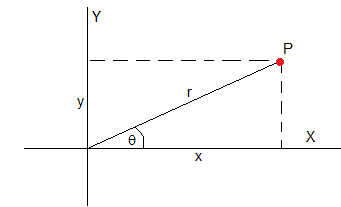
Dado la abscisa x y la ordenada y de un punto P, se pide calcular su distancia r al origen y el ángulo θ que forma con el eje X. Transformar las coordenadas del punto P de rectangulares a polares

$r = \sqrt{x^{2} + y^{2}} \tan θ = \frac{y}{x}$

x=input('Abscisa x: ');
y=input('Ordenada y: ');
r=sqrt(x^2+y^2);
if x>=0
    theta=atan(y/x);
    if y<0
        theta=theta+2*pi;
    end
else
    theta=atan(y/x)+pi;
end
fprintf('La distancia es %1.2f y el ángulo es %3.2f\n',r,theta*180/pi)

Abscisa x: -2
Ordenada y: -3
La distancia es 3.61 y el ángulo es 236.31
>> atan2(-3,-2)*180/pi+360
ans =  236.3099

La función atan2(y,x) nos proporciona también el ángulo en radianes

Es importante la identación para entender el código, tal como se muestra en este script. De este modo, vemos la sentencia o sentencias que se ejecutan en cada bloque if. MATLAB selecciona el código con la combinación de teclas Ctrl+a y lo dispone adecuadamente con la combinación Ctrl+i.

if...else

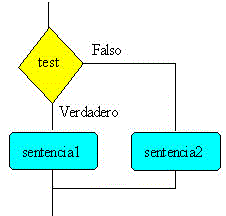
La sentencia if...else completa la sentencia if, para realizar una acción alternativa

Si la condición es verdadera se ejecuta las sentencias 1. La palabra clave else, significa que si la condición no es verdadera se ejecuta las sentencias 2, tal como se ve en la figura.

if condicion
    sentencias_1
else
    sentencias_2
end

Definición de funciones

La función que calcula el signo de un número se define de la siguiente forma: sign(x) devuelve -1 si x es menor que 0, 1 si x es mayor que 0, y 0 en el otro caso. Creamos nuestra propia función que denominaremos signo(x) que se comporta igual que la función MATLAB sgn(x)

Creamos una funcion denominada signo, a la que se le pasa un escalar y devuelve 1, 0 ó -1. La guardamos en el fichero signo.m

function sgn = signo(x)
    if x > 0
        sgn = 1;
    elseif x < 0
        sgn = -1;
    else
        sgn = 0;
    end
end

Probamos la función signo en la ventana de comandos

>> signo(-2)
ans = -1
>> signo(0)
ans = 0
>> signo(4)
ans = 1

Definimos la siguiente función

$f (x) = {\begin{cases} 0 x < 0 \\ x 0 \leq x \leq 1 \\ 2 - x 1 < x \leq 2 \\ 0 x > 2 \end{cases}$

Vamos a trasladar la definición matemática a código, escribiendo en el editor de funciones

function y=f(x)
    if x>=0 & x<=1
        y=x;
    elseif x>1 & x<=2
        y=2-x;
    else
        y=0;
    end
end

Probamos la función en la ventana de comandos

>> f(-1)
ans = 0
>> f(0.5)
ans = 0.5000
>> f(1.8)
ans = 0.2000

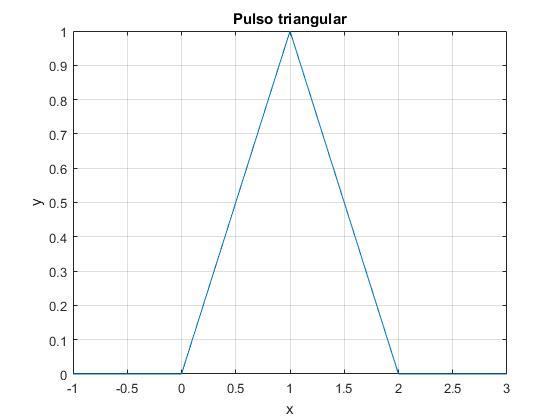
Representamos gráficamente la función f en el intervalo (-1,3)

>> fplot(@f,[-1,3])
>> grid on
>> xlabel('x')
>> ylabel('y')
>> title('Pulso triangular')

Sistemas de ecuaciones lineales

En la página Ecuaciones y sistemas consideraremos un sistema de ecuaciones lineales que podemos escribir Ax=b, donde A es una matriz de dimensión m×n, y x y b son dos vectores columna de longitudes n y m respectivamente. Tenemos un sistema de m ecuaciones con n incógnitas.

El sistema tiene solución si y solo si el rango de la matriz A es igual al rango de la matriz aumentanda A|b.
Si el rango es igual al número n de incógnitas el sistema tiene una solución única.
Si el rango es menor que el número n de incógnitas entonces hay un número infinito de soluciones

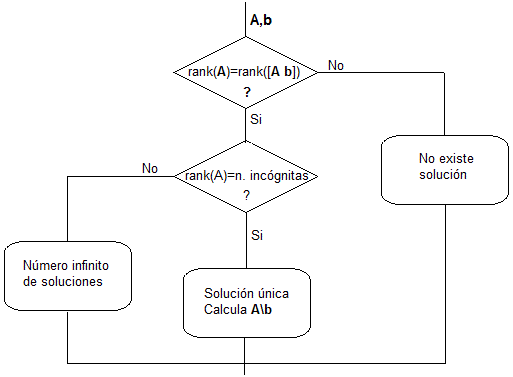
Vamos a escribir una función denominada sistema_ecuaciones, al cual le pasamos las matrices A y b y nos imprime un mensaje si el sistema de ecuaciones no tiene solución o hay un número infinito de soluciones y nos devuelve la solución si es única.

function x =sistema_ecuaciones(A,b)
    rango_A=rank(A);
    rango_Ab=rank([A b]);
    [m,n]=size(A);
    fprintf('Sistema de %i ecuaciones con %i incógnitas\n',m,n);
    if rango_A~=rango_Ab
        disp('El sistema no tiene solución')
    elseif rango_A==n
        disp('Hay una solución única')
        x=A\b;
    elseif rango_A<n
        disp('Hay infinitas soluciones');
    end
end

En la ventana de comandos probamos la función sistema_ecuaciones, con los mismos ejemplos utilizados en la página Matrices.

>> A=[2 1; 2 -1; 1 -2];
>> b=[3;0;4];
>> sistema_ecuaciones(A,b)
Sistema de 3 ecuaciones con 2 incógnitas
El sistema no tiene solución
>> A=[2 1; 2 -1; 1 -2];
>> b=[3;5;4];
>> sistema_ecuaciones(A,b)
Sistema de 3 ecuaciones con 2 incógnitas
Hay una solución única
ans =
    2.0000
   -1.0000
>> A=[2 1; 4 2; 6 3];
>> b=[3;6;9];
>> sistema_ecuaciones(A,b)
Sistema de 3 ecuaciones con 2 incógnitas
Hay infinitas soluciones

switch

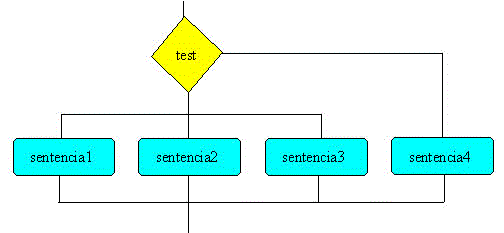
Como podemos ver en la figura del apartado anterior, la sentencia if...elseif...else tiene varias ramas, el programa va por una u otra rama dependiendo del valor verdadero o falso de la expresión evaluada. A veces, es necesario, elegir entre varias alternativas, como se muestra en la siguiente figura

Por ejemplo, considérese las siguientes series de sentencias if...else

if condicion_1
    sentencias_1
elseif condicion_2
    sentencias_2
elseif condicion_3
    sentencias_3
else
    sentencias_4
end

El código resultante puede ser difícil de seguir y confuso incluso para el programador avanzado. MATLAB proporciona una solución elegante a este problema mediante la sentencia condicional switch para agrupar a un conjunto de sentencias if...else.

switch expresion 
    case valor1
        sentencias_1
    case valor2
        sentencias_2
    case valor3
        sentencias_3
    otherwise
        sentencias_4
end

En la sentencia switch, se compara el valor de una variable o el resultado de evaluar una expresión, con un conjunto de valores valor1, valor2, valor3, .., cuando coinciden se ejecuta el bloque de sentencias que están asociadas. Si el compilador no encuentra coincidencia, se ejecuta la sentencia otherwise, si es que está presente en el código.

Longitud de una circunferencia, área de un círculo

La función strcmp compara dos cadenas de caracteres devolviendo 1 si son idénticas y 0 si no los son.

Definimos una función, que toma el radio r y una cadena de caracteres str y devuelve la longitud de la circunferencia si str='circunferencia', el área si str='circulo', ó -1 si no es una de las dos cosas

function z = calcula_1(r,str)   
    if strcmp(str, 'circunferencia')
        z=2*pi*r;
    elseif strcmp(str,'circulo')
        z=pi*r^2;
    else
        z=-1;
    end
end

>> calcula_1(3,'circulo')
ans =   28.2743
>> calcula_1(3,'circunferencia')
ans =   18.8496
>> calcula_1(3,'circu')
ans =    -1

Alternativamente, se puede emplear la sentencia condicional switch

function z = calcula(r,str)
    switch str
        case 'circunferencia'
            z=2*pi*r;
        case 'circulo'
            z=pi*r^2;
        otherwise
            z=-1;
    end
end

Calendario

En el script meses, se introduce el nombre del mes y se guarda en la variable nMes. Cuando se especifica en el comando input el parámetrro 's' no es necesario introducir el nombre entre comillas simples.

A continuación, se utiliza solamente los tres primeros caracteres que se convierten con la función lower a minúsculas. Si se introduce el mes de febrero pregunta si es o no bisiesto. De nuevo, tomamos la primera letra en minúscula como respuesta s o n y la guardamos en la variable bi. Se presentan tres posibilidades, que el mes tenga 31 días, que el mes tenga 30 o que el mes sea febrero con dos posibilidades si es bisiesto tiene 29 días en caso contrario tiene 28 días.

nMes=input('Introduce el nombre del mes): ','s');
mes=lower(nMes(1:3)); %utiliza las tres primeras letras del mes
if mes=='feb' %utilizar strcmp(mes,'feb') para comparar strings
    bisiesto=input('¿Es año bisiesto?:','s');
	bi=lower(bisiesto(1)); %utiliza la primera letra
end
switch mes
    case{'sep','abr','jun','nov'}
         dias=30
    case 'feb'
        if bi=='s'
            dias=29
        else
            dias=28
        end
    otherwise
        dias=31
end

Cuando se comparan cadenas de caracteres (string) es conveniente utilizar la función strcmp de modo que la sentencia if mes=='feb' se sustituye por if strcmp(mes,'feb'), de este modo el compilador de MATLAB elimina el aviso (raya de color anaranjado en la parte derecha de la ventana del Editor)

>> meses
Introduce el nombre del mes: febrero
¿Es año bisiesto? (s/n):No
dias =    28
>> meses
Introduce el nombre del mes: Julio
dias =    31

Meses y días de cada mes

Ahora un ejemplo más complicado, escribir un programa que calcule el número de días de un mes determinado cuando se proporciona el año.

Se anota primero, los meses que tienen 31 días y los que tienen 30 días. El mes de Febrero (2° mes) es el más complicado ya que tiene 28 días excepto en los años que son bisiestos que tiene 29. Son bisiestos los años múltiplos de cuatro, que no sean múltiplos de 100, pero si son bisiestos los múltiplos de 400.

mes=input('introduce un número (1-12): ');
anho=input('introduce el año: ');
numDias=30;
switch mes
    case {1,3,5,7,8,10,12}
        numDias = 31;
    case {4,6,9,11}
        numDias = 30;
    case 2
        if ( (rem(anho,4) == 0 & ~(rem(anho,100) == 0)) | rem(anho,400) == 0 )
            numDias = 29;
        else
            numDias = 28;
        end
    otherwise
        disp('Este mes no existe')
end
fprintf('El mes %i del año %i tiene %i días\n',mes,anho,numDias)

rem(a,b) devuelve el resto de la división entre dos números a y b. Por ejemplo

>> rem(23,4)
ans = 3

Podemos convertir el código del script en una función denominada calendario de modo que al pasarle el mes y el año nos devuelva el número de días

function numDias=calendario(mes, anho)
    switch mes
        case {1,3,5,7,8,10,12}
            numDias = 31;
        case {4,6,9,11}
            numDias = 30;
        case 2
            if ( (rem(anho,4) == 0 & ~(rem(anho,100) == 0)) | rem(anho,400) == 0 )
                numDias = 29;
            else
                numDias = 28;
            end
        otherwise
            disp('Este mes no existe')
    end
end

Probamos la función calendario en la ventana de comandos

>>calendario(2,1900)
ans = 28
>>calendario(2,2000)
ans = 29
calendario(10,2013)
ans = 31

Ejemplos

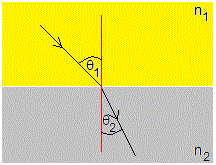
1.-Cálculo del ángulo del rayo refractado

La ley de Snell de la refracción es n₁·sinθ₁=n₂·sinθ₂.

Si n₁<n₂, el ángulo θ₂ del rayo refractado es menor que el incidente θ₁
Si n₁>n₂, el ángulo θ₂ del rayo refractado es mayor que el incidente θ₁. Para el angulo incidente crítico n₁·sinθ_c=n₂, el ángulo refractado es θ₂=90°. Si el ángulo incidente θ₁>θ_c, no hay rayo refractado, solamente reflejado θ₂=θ₁.

n1=1.5; %indice de refracción del medio 1
n2=1;  %indice de refracción del medio 2
ang1=30; %ángulo incidente
if n1<n2
    ang2=asind(n1*sind(ang1)/n2);
    disp(['Angulo refractado: ', num2str(ang2)])
else
    aCritico=asind(n2/n1);
    if ang1>aCritico
        disp(['Angulo reflejado: ', num2str(ang1)])
    else
        ang2=asind(n1*sind(ang1)/n2);
        disp(['Angulo refractado: ', num2str(ang2)])
    end
end