plot

Definimos un vector de datos, en la ventana Workspace pulsamos el botón derecho del ratón cuando el puntero está situado sobre el nombre de la variable y que guarda dichos datos. Seleccionamos en el menú flotante plot(y) para obtener la representación gráfica que vemos más abajo.

>>  y=[0,0.38,0.71,0.92,1.00,0.92,0.71,0.38,0];

La representación gráfica es

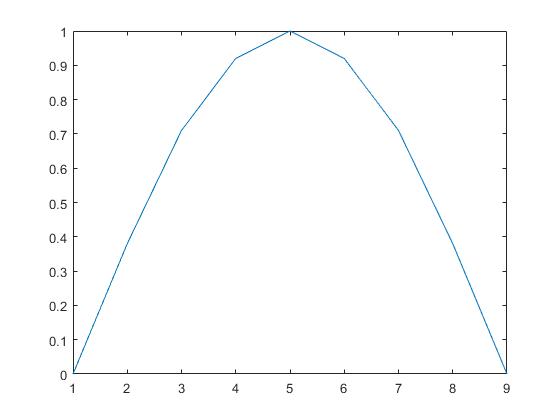
En la ventana de comandos obtenemos la misma representación llamando al comando plot.

>>  y=[0,0.38,0.71,0.92,1.00,0.92,0.71,0.38,0];
>> plot(y)

El comando plot(x,y) se utiliza para crear una representación gráfica bidimensional, donde x e y son vectores. Si se pasa solamente el vector y de los datos, plot(y), MATLAB entiende que x es el vector de los índices x=[1,2,3...]; tal como vemos en la figura anterior. Sea ahora,

>> x=[0 10 20 30 40 50 60 70 80];
>> y=[0 0.73 1.10 1.29 1.40 1.46 1.50 1.52 1.53];
>> plot(x,y)

Esto es todo lo que se precisa para hacer representación gráfica en la ventana denominada Figure Window: Proporcionar los vectores de datos x e y (que tienen que tener el mismo número de elementos) y la llamada al comando plot. Las decoraciones del gráfico (etiquetas en el eje X y en el eje Y, título, etc.) se pueden hacer mediante llamadas a comandos (xlabel, ylabel, title, etc.) o en la propia ventana gráfica, seleccionando los elementos apropiados del menú, en particular Tools->Edit Plot.

El comando plot tiene parámetros adicionales que nos permiten especificar el color y tipo de línea o los símbolos utilizados como marcadores. Por ejemplo

plot(x,y,'-mo','linewidth',2,'markersize',12, 'markeredgecolor','g','markerfacecolor','y')

Los dos primeros parámetros de plot son las coordenadas de los puntos (x_i, y_i) guardados en los vectores x e y. El tercer parámetro es el especificador de línea que puede contener tres datos '-mo' entre comillas simples:

• Estilo de línea (- significa sólido, por defecto)
• Color de línea (m significa magenta)
• Marcador (o significa círculo)

Las posibles opciones son:

Opciones de símbolos para marcar puntos en la gráfica

Se pueden también especificar las siguientes propiedades entre comillas simples y a continuación, sus valores:

• linewidth, especifica la anchura de línea su valor por defecto es 0.5
• markersize, especifica el tamaño del símbolo que marca los puntos
• markeredgecolor, especifica el color de borde del símbolo que marca los puntos
• markerfacecolor, especifica el color de relleno del símbolo que marca los puntos

Ejemplos de plot:

• plot(x,y), una línea azul sólida concecta los puntos (x_i, y_i)
• plot(x,y,'r'), una línea roja sólida conecta los puntos (x_i, y_i)
• plot(x, y,':g'), una línea de puntos de color verde conecta los puntos (x_i, y_i)
• plot(x,y,'--ro','linewidth',2,'markersize',8), ejemplo más abajo

Vectores de datos

En un experimento de carga de un condensador se ha medido la diferencia de potencial V entre las placas del condensador en función del tiempo t, desde que se conecta la batería.

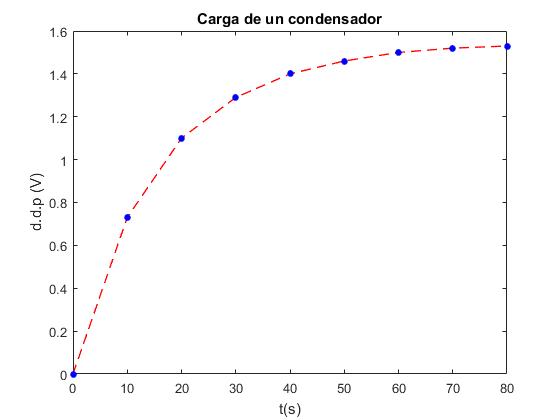
t=[0 10 20 30 40 50 60 70 80];
V=[0 0.73 1.10 1.29 1.40 1.46 1.50 1.52 1.53];
plot(t,V,'--ro','linewidth',1,'markersize',4,'markeredgecolor'
,'b','markerfacecolor','b')
title('Carga de un condensador')
xlabel('t(s)')
ylabel('d.d.p (V)')

En un experimento de descarga de un condensador se ha medido la diferencia de potencial V entre las placas del condensador en función del tiempo t.

Crear una tabla de datos y un gráfico, similar al de la figura anterior.

Gráfica de una función

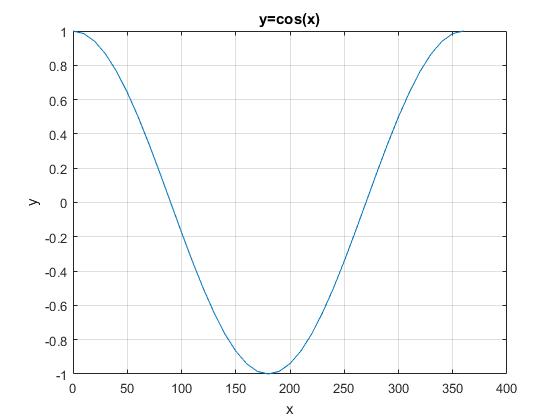
Vamos a obtener una tabla de datos de la función coseno, utilizando como argumento grados, cosd(x) y representarla en el intervalo de 0 a 360°, tomando un intervalo de 10°

x=0:10:360;
y=cosd(x);
plot(x,y)
grid on %rejilla
title('y=cos(x)')
xlabel('x')
ylabel('y')

Función definida en forma paramétrica

Representaremos las denominadas figuras de Lissajous, que se observan en la pantalla de un osciloscopio, cuando se introducen señales senoidales de la misma o de distinta frecuencia por las entradas X e Y.

x=Asin(ω_xt)
y=Asin(ω_yt+δ)

wx=input('Frecuencia angular X: ');
wy=input('Frecuencia angular Y: ');
delta=input('Desfase (grados): ');
t=0:360;
x=sind(wx*t);
y=sind(wy*t+delta);
plot(x,y,'r');
text(0,0.2,'\omega_x/\omega_y=2/1')
xlabel('x'); 
ylabel('y')
title('Figuras de Lissajous')

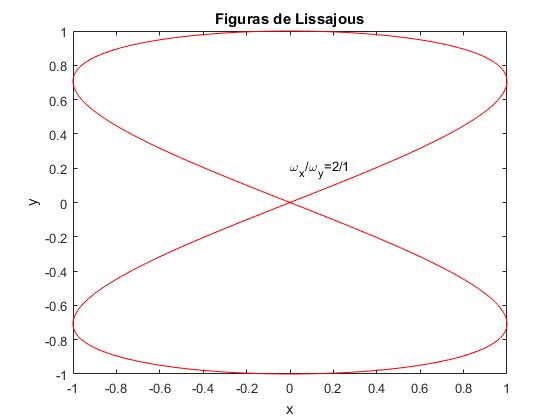
Introducimos los valores de las frecuencias angulares ω_x,ω_y y del desfase δ

Frecuencia angular X: 2
Frecuencia angular Y: 1
Desfase (grados): 90

El comando text permite escribir un mensaje (caracteres entre comillas simples) en las coordendas x e y especificadas. En este caso, el mensaje consiste en el cociente de frecuencias angulares ω_x/ω_y.

Para escribir una letra griega se antepone el carácter \. Por ejemplo, α es \alpha, ω es \omega, etc. Para poner un subíndice se antepone el caracter _. Por ejemplo para que aparezca x₁ se escribe x_1

Funciones simétricas y antisimétricas

Queremos representar una función f(x) simétrica f(-x)=f(x) o antisimétrica f(-x)=-f(x) entre -a y +a. Debido a la simetría, solamente es necesario calcular los valores de la función en el intervalo 0≤x<a. Esto evita repetir dos veces el mismo cálculo.

Por ejemplo, cos(x) es una función simétrica, calculamos sus valores para x≥0

x=[30,60,90]*pi/180;
xx=[-fliplr(x),0,x];
f=@(x) cos(x);
y=f(x);
yy=[fliplr(y),f(0),y];
disp([xx*180/pi;yy])

Ordendos en columnas, aparece el ángulo x en grados y debajo el valor de su coseno, cos(x)

  -90.0000  -60.0000  -30.0000         0   30.0000   60.0000   90.0000
    0.0000    0.5000    0.8660    1.0000    0.8660    0.5000    0.0000

Para representar estas funciones utilizamos la función fliplr, véase la página titulada Vectores

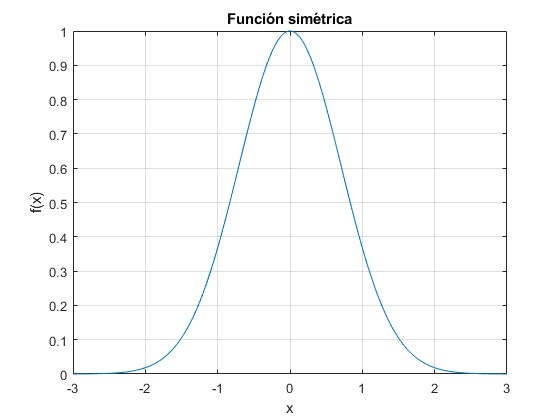
x=linspace(0,3,200);
y=exp(-x.^2); %simétrica
yy=[fliplr(y),y];
xx=[-fliplr(x),x];
plot(xx,yy)
grid on
xlabel('x')
ylabel('f(x)')
title('Función simétrica')

x=linspace(0,3,200);
y=x.*exp(-x.^2); %antisimétrica
yy=[-fliplr(y),y];
xx=[-fliplr(x),x];
plot(xx,yy)
grid on
xlabel('x')
ylabel('f(x)')
title('Función antisimétrica')

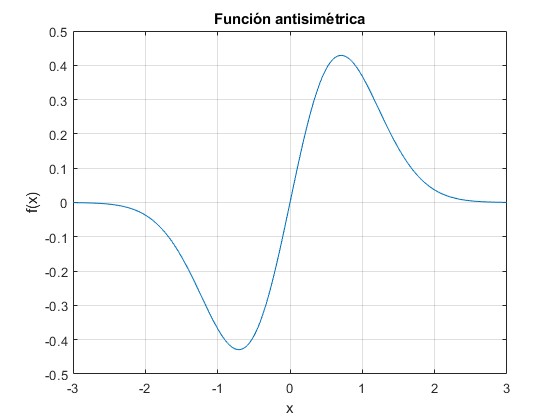
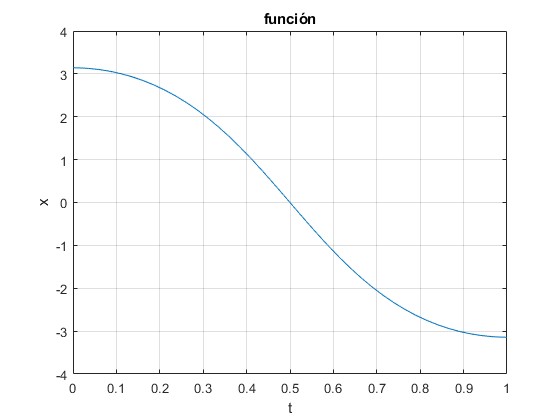
La función x=cos(πt) repite los valores entre t=0 y t=1/2 cambiados de signo en el intervalo t=1/2 a t=1.

Resolvemos la ecuación diferencial del movimiento de un cuerpo entre los instantes t=0, y t=1/2, por simetría, las posiciones se repiten con el signo cambiado entre t=1/2 y t=1. De modo que la posicón en el instante t=0.4 es la misma (cambiada de signo) que en el instante t=0.6 y así, sucesivamente. Evitamos resolver la ecuación diferencial en el intervalo [1/2,1] del siguiente modo

t=[0;0.0000;0.0043;0.0057;0.0071;0.0142;0.0213;0.0284;0.0355;0.0605;0.0855;
0.1105;0.1355;0.1605;0.1855;0.2105;0.2355;0.2605;0.2855;0.3105;0.3355;0.3605;
0.3855;0.4105;0.4355;0.4516;0.4677;0.4839;0.5000];
x=[3.1416;3.1415;3.1414;3.1412;3.1410;3.1394;3.1366;3.1327;3.1276;3.1010;3.0601;
3.0047;2.9343;2.8484;2.7464;2.6275;2.4912;2.3368;2.1638;1.9719;1.7612;1.5321;
1.2857;1.0236;0.7483;0.5651;0.3786;0.1899;-0.0000];

xx=[x;-x(length(x):-1:1)];
tt=[t; 1-t(length(t):-1:1)];
plot(tt,xx)
grid on
xlabel('t')
ylabel('x')
title('función')

Fijarse que los vectores t y x son vectores columna

Varias gráficas en la misma ventana

La ecuación de una oscilación amortiguada es

x=Bexp(-γ·t)·sin(ωt+δ)

donde B y δ se determinan a partir de las condiciones iniciales

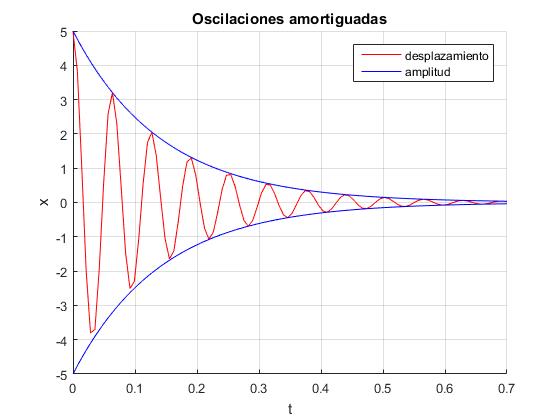
Sea la oscilación amortiguada

x=5.0·exp(-7·t)·sin(100·t+1.5)

Queremos representar a la vez,

• El desplazamiento x en función del tiempo t
• La amplitud A=5.0·exp(-7·t), en función del tiempo t

Ulizamos el comando hold on para representar varias gráficas en la misma ventana.

t=linspace(0,0.7,100);
A=5*exp(-7*t);
x=A.*sin(100*t+1.5); 

hold on
plot(t,x,'r')
plot(t,A,'b') 
plot(t,-A,'b')
hold off

grid on
legend('desplazamiento','amplitud')
title('Oscilaciones amortiguadas')
xlabel('t')
ylabel('x') 

Una forma alternativa utilizando el comando plot

t=linspace(0,0.7,100);
A=5*exp(-7*t);
x=A.*sin(100*t+1.5); 
% (t,x) en  rojo 'r', (t,A) en azul 'b', (t,-A) sigue en azul
plot(t,x,'r',t,A,'b',t,-A)
legend('desplazamiento','amplitud')
title('Oscilaciones amortiguadas')
xlabel('t')
ylabel('x') 

O bien, guardando los datos de la oscilación amortiguada x y de la amplitud A (positiva y negativa) en un vector z.

t=linspace(0,0.7,100);
A=5*exp(-7*t);

z=[A.*sin(100*t+1.5);A;-A];

plot(t,z) 
legend('desplazamiento','amplitud')
title('Oscilaciones amortiguadas')
xlabel('t')
ylabel('x') 

De forma equivalente

t=linspace(0,0.7,100);
A=5*exp(-7*t);

z(1,:)=A.*sin(100*t+1.5);
z(2,:)=A;
z(3,:)=-A;

plot(t,z) 
legend('desplazamiento','amplitud')
title('Oscilaciones amortiguadas')
xlabel('t')
ylabel('x') 

Otra forma, utilizando el comando line

t=linspace(0,0.7,100);
A=5*exp(-7*t);
x=A.*sin(100*t+1.5); 
plot(t,x,'r')
line(t,A,'color','b') 
line(t,-A)
legend('desplazamiento','amplitud')
title('Oscilaciones amortiguadas')
xlabel('t')
ylabel('x')

Los dos primeros parámetros del comando line son los vectores x e y de datos. Los siguientes son propiedad entre comillas simples, seguido del valor de la propiedad, por ejemplo:

line(x,y,'linestyle','--','color','r','marker','o')

La diferencia principal entre plot y line, es que plot abre una ventana gráfica cada vez que es ejecutado, mientas que line añade gráficas a la ventana abierta previamente con plot, como en el script anterior

Decorando las gráficas

Ya hemos visto el efecto de xlabel, ylabel, title y legend en el ejemplo anterior para poner un título a la gráfica (title), identificar el eje X (xlabel) el eje Y (ylabel) y cada una de las gráficas en la misma ventana (legend)

legend

El comando legend es más complejo que los otros comandos y admite la forma siguiente:

legend('grafica1','grafica2')

El orden en el que se ponen las etiquetas corresponde al que se crean las gráficas. En el ejemplo anterior, primero se crea la gráfica de la posición (t,x) y después las dos gráficas de la amplitud (t,A)

legend('desplazamiento','amplitud','location','northwest')

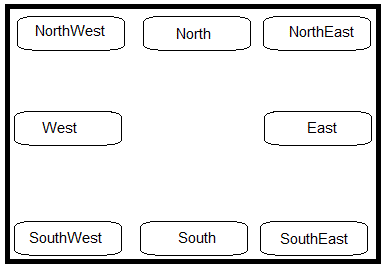
En la figura se muestra algunos de los posibles valores del parámetro location y la ubicación de las etiquetas. Otro posibles valores son: Best, MATLAB determina la mejor ubicación de las etiquetas para que interfiera lo mínimo con las gráficas. También se pueden poner fuera de las gráficas, con los valores NorthOutside, SouthOutside, NorthEastOutside...BestOutside

axis

Cuando se ejecuta el comando plot(x,y) MATLAB crea un eje X y un eje Y cuyos límites se deducen a partir de los valores máximo y mínimo de cada uno de los vectores x e y.

El comando axis permite cambiar el rango y la apariencia de los ejes

• axis([xmin,xmax,ymin,ymax]), establece nuevos límites a los ejes X e Y
• axis equal, establece la misma escala para ambos ejes
• axis square, región cuadrada

Probamos el aspecto de una elipse de semieje mayor 2 y semieje menor 1 según los ejes

>> t=0:pi/40:2*pi;
>> plot(2*sin(t),cos(t))
>> xlabel('2·sin(t)')
>> ylabel('cos(t)')
>> axis equal
>> axis square

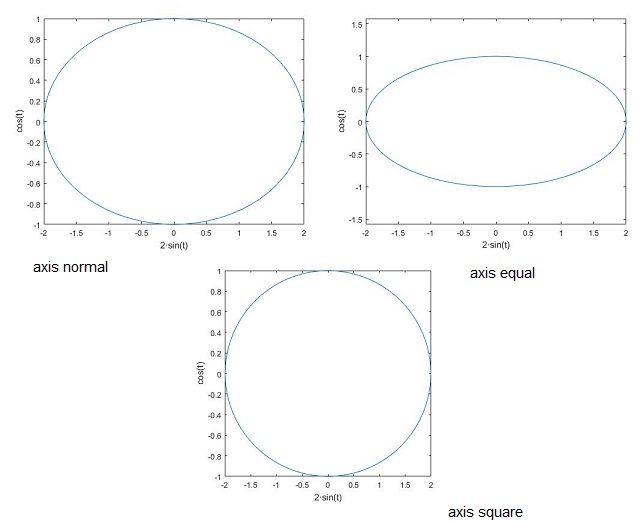
Como apreciamos axis equal preserva las misma unidad en el eje X y en el eje Y, lo que es importante para representar figuras como una elipse sin distorsión

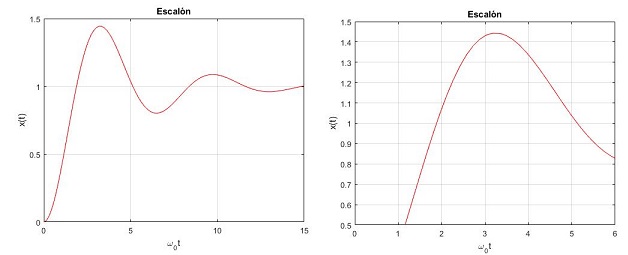
Autoescalado

En la figura de la izquierda (más abajo) no hemos utilizado el comando axis para poner límites a los ejes, MATLAB los establece a partir de los valores máximo y mínimo de X y de Y. Sin embargo, en la figura de la derecha hemos establecido límites a los ejes: ymin=0.5 e ymax=1.5, el límite xmax=6, pero no hemos establecido un xmin concreto. Poniendo xmin=-Inf (menos infinito) dejamos a MATLAB que escale la figura. El efecto lo vemos comparando ambas figuras.

g=0.25;
t=linspace(0,15,100); 
w=sqrt(1-g^2);
x=1-exp(-g*t).*(g*sin(w*t)/w+cos(w*t));
plot(t,x,'r')
axis([-Inf,6,0.5,1.5])
title('Escalón')
xlabel('\omega_0t')
ylabel('x(t)')
grid on

xlim, ylim

Establece los límites en el eje horizontal X y en el vertical Y. Por ejemplo, xlim([0, 12]) indica el valor mínimo y máximo de la abscisa que se va a representar en la ventana gráfica.

grid

grid on, añade una rejilla a la gráfica como en la primera figura

grid off, (por defecto) no añade la rejilla

text

Para poner un texto en la figura en la posición especificada por las coordendas x e y.

text(x,y,'mensaje')

El primer carácter del texto que se le pasa a text entre comillas simples se pone en el punto de coordendas (x,y)

El texto que se le pasa a los comandos xlabel, ylabel, title y text, puede contener caracteres de distinta fuente de texto y tamaño, letra en negrita, cursiva; subíndices y superíndices, caracteres griegos. El texto incluso se puede rotar para que aparezca vertical o en otra orientación.

Por ejemplo, para cambiar la fuente de texto por defecto a otra de mayor tamaño, 18 puntos, se escribe

text(x,y,'mensaje','FontSize',18)

En el programa que dibuja las figuras de Lissajous hemos utilizado el comando text

Algunos caracteres griegos y símbolos matemáticos

Se puede mostrar un solo carácter como subíndice o superíndice, a continuación del símbolo ^ o _. Se pueden mostrar varios caracteres como subíndices o superíndices si se ponen entre corchetes, por ejemplo y^{2n-1}, se muestra y^2n-1, g_{01}(x), se muestra g₀₁(x)

fplot

La función fplot dibuja una gráfica si se le pasa la función f en el primer parámetro y el intervalo [x_min, x_máx] en el segundo

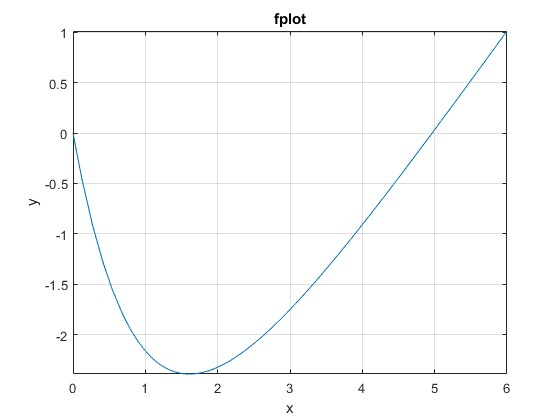
f=@(x) x-5*(1-exp(-x));
fplot(f,[0 6]);
xlabel('x')
ylabel('y')
title('fplot')
grid on

Hay diferencias significativas entre plot y fplot. La primera evalúa la función para valores de x igualmente espaciados. Como vemos hay que especificar el intervalo Δx o el número de puntos, mientras que en la segunda no es necesario especificarlo. fplot evalúa internamente la función más frecuentemente en aquellas regiones en las que cambia rápidamente. En el siguiente ejemplo se dibuja la siguiente función en el intervalo [0.01 0.1]

${\displaystyle y=\sin \left(\frac{1}{x}\right)}$

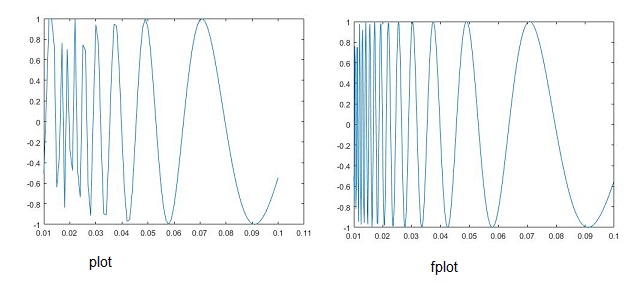
>> x=0.01:0.001:0.1;
>> y=sin(1./x);
>> plot(x,y)

Tomando Δx=0.001, se obtiene una figura con baja resolución (izquierda). Sin embargo,

>> fplot(@(x) sin(1./x),[0.01 0.1])

Obtenemos una figura con mejor resolución (derecha) sin tener que probar distintos valores de Δx o del número de puntos.

Así pues, fplot presenta ventajas frente a plot

Otra forma alternativa de obtener la gráfica de la derecha

>> fplot(@(x) sin(1./x),[0.01,0.1])

que es equivalente a

>> f=@(x) sin(1./x);
>> fplot(f,[0.01,0.1])

Para mostrar varias gráficas en la misma ventana

>> fplot(@(x)[sin(x),cos(x),tan(x)], [0,2*pi,-2,2])

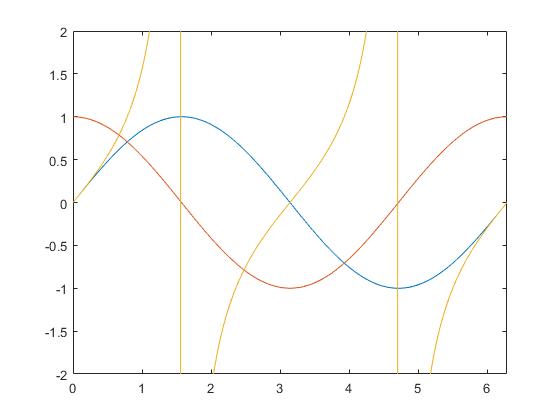
Entre corchetes, 0 a 2·π es el intervalo horizontal, en eje X, mientras que -2 a 2 es el intervalo vertical, en el eje Y

Curva paramétrica

La curva cicloide viene definida por dos ecuaciones que dependen de un parámetro θ

x=r(θ-sinθ)
y=r(cosθ-1)

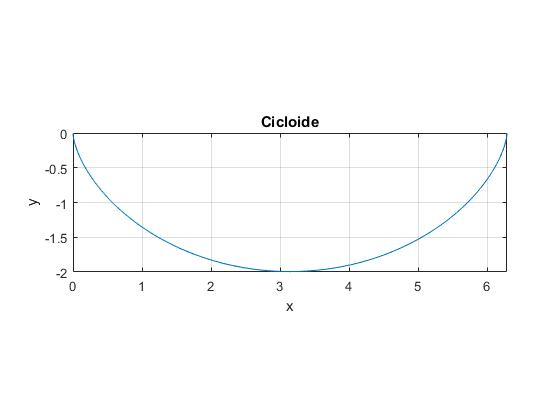
r=1;
x=@(t) r*(t-sin(t));
y=@(t) r*(cos(t)-1);
fplot(x,y,[0,2*pi])
axis equal
grid on
xlabel('x'); 
ylabel('y')
title('Cicloide')

Gráficos con dos ejes Y

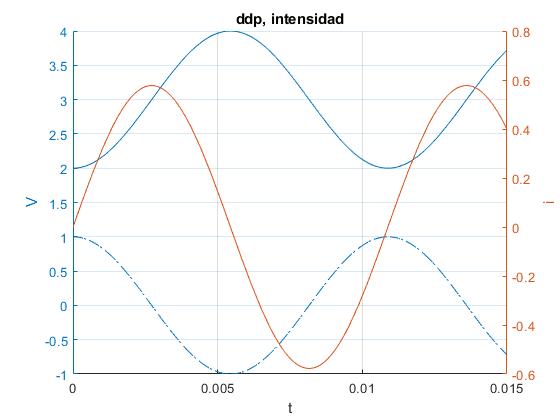
Representamos V₁ y V₂, diferencia de potencial entre las placas de los dos condensadores. En el mismo gráfico, representamos la intensidad i₁

Para asociar un elemento gráfico con el eje Y izquierdo se emplea yyaxis left y con el derecho, yyaxis right

C=1e-3; %capacidad
L=1e-3; %autoinducción
w=1/sqrt(3*C*L); %frecuencia angular
V0=3; %fem batería
i0=V0*sqrt(C/L)/(3*sqrt(3));
hold on
yyaxis left
fplot(@(t) V0*(1-cos(w*t)/3),[0,15/1000]) %V1
fplot(@(t) V0*cos(w*t)/3,[0,15/1000]) %V2
yyaxis right
fplot(@(t) i0*sin(w*t),[0,15/1000]) %i1
hold off
xlabel('t')
yyaxis left
ylabel('V')
yyaxis right
ylabel('i')
grid on
title('ddp, intensidad')

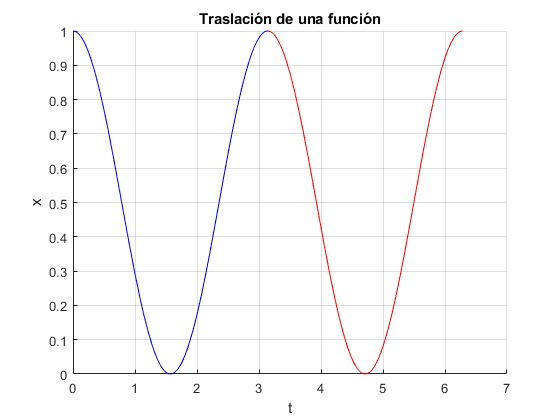
Traslación de una función

Dada la función f(t) queremos representar la función f(t+T)

hold on
h=fplot(@(t) cos(t).^2,[0,pi], 'color','b');
plot(h.XData+pi,h.YData, 'r')
hold off
grid on
xlabel('t')
ylabel('x')
title('Traslación de una función')

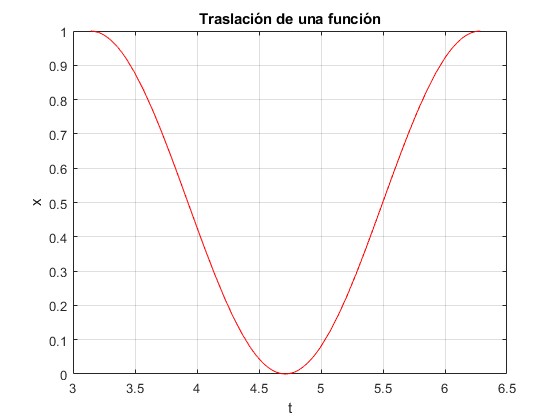
Si no queremos representar la función original, solamente la trasladada

h=fplot(@(t) cos(t).^2,[0,pi], 'color','b');
h.Visible=false;
plot(h.XData+pi,h.YData, 'r')
grid on
xlabel('t')
ylabel('x')
title('Traslación de una función')

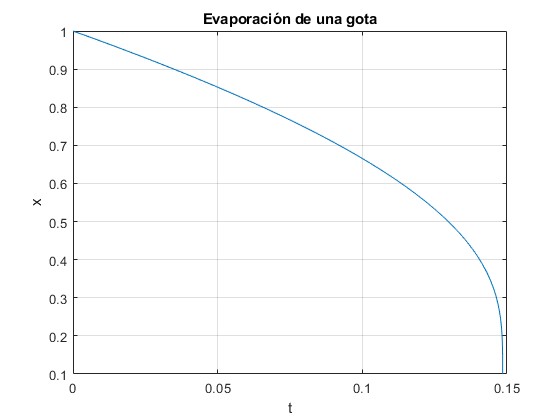
Funciones implícitas, fimplicit

La función implícita que vamos a representar es

${\displaystyle t=\text{Ei}\left(-1\right)+\frac{1}{e}-\text{Ei}\left(-\frac{1}{x}\right)-x\exp \left(-\frac{1}{x}\right)}$

t=@(x) ei(-1)+1/exp(1)-ei(-1./x)-x.*exp(-1./x);
fp=fplot(t,[0.1,1]);
plot(fp.YData, fp.XData)
grid on
xlabel('t')
ylabel('x')
title('Evaporación de una gota')

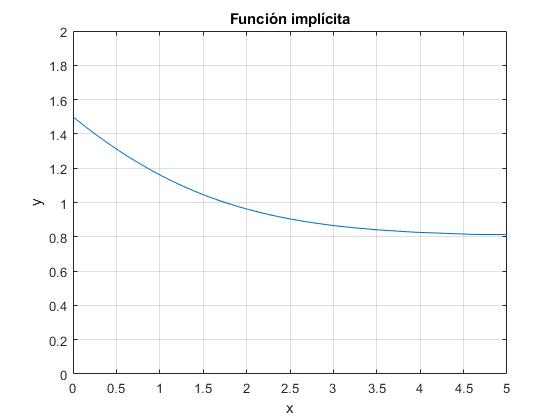
Vamos representar la función implícita f(x,y)=0, en el intervalo [x₁, x₂, y₁, y₂] mediante el comando fimplicit. Sea la función implícita

${\displaystyle \ln \frac{k-y_0}{k-y}+y_0-y-x=0}$

Representamos esta función para k=0.8 e y₀=1.5 en el intervalo a lo largo del eje X [0,5] y a lo largo del eje Y [0,2]

k=0.8;
y0=1.5;
f=@(x,y) log((k-y0)./(k-y))+y0-y-x;
fimplicit(f,[0,5,0,2])
grid on
xlabel('x')
ylabel('y')
title('Función implícita')

Varias ventanas gráficas, figure

Es posible abrir varias ventanas gráficas mediante el comando figure. MATLAB nombra cada ventana como Figure 1, Figure 2, Figure 3, etc.

Las ventanas gráficas se pueden cerrar con el comando close que cierra la ventana activa, close(n) cierra la ventana n y close all cierra todas las ventanas gráficas

Creamos un script para abrir cuatro ventanas gráficas

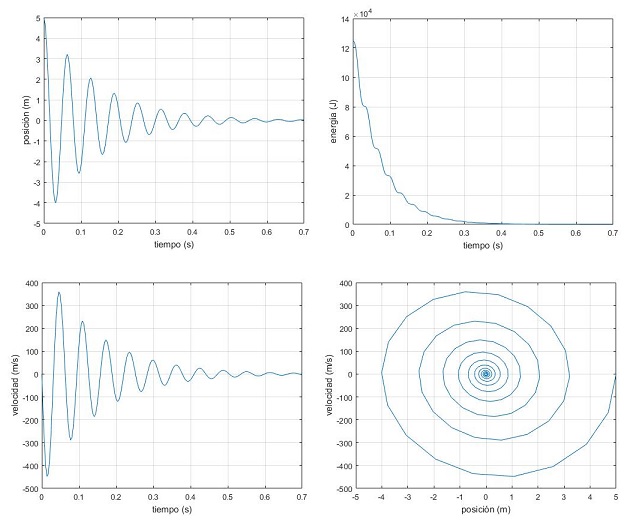
1. Representar en la primera, la posición x en función del tiempo t
2. Representar en la segunda, la energía e del oscilador en función del tiempo t
3. Representar en la tercera, la velocidad v del móvil en función del tiempo t
4. Respresentar en la cuarta, la velocidad del móvil v en función de su posición x (espacio de las fases)

g=7; %amortiguamiento
x0=5; %posición inicial 
v0=0; %velocidad inicial
w0=100;  %frecuencia natural
w=sqrt(w0^2-g^2); %frecuencia
x=@(t) exp(-g*t).*((v0+g*x0)*sin(w*t)/w+x0*cos(w*t));
v=@(t) -g*x(t)+exp(-g*t).*((v0+g*x0)*cos(w*t)-x0*w*sin(w*t));
e=@(t) (v(t).^2+w0*w0*x(t).^2)/2;

fplot(x,[0,0.7])
grid on
xlabel('tiempo (s)')
ylabel('posición (m)')

figure
fplot(e,[0,0.7])
grid on
xlabel('tiempo (s)')
ylabel('energía (J)')

figure
fplot(v,[0,0.7])
grid on
xlabel('tiempo (s)')
ylabel('velocidad (m/s)')

figure
t=linspace(0,0.7,200);
plot(x(t),v(t))
grid on
xlabel('posición (m)')
ylabel('velocidad (m/s)')

Corremos el script y nos aparecen cuatro ventanas gráficas: Figure 1, Figure 2, Figure 3 y Figure 4.

Cerramos todas las ventanas gráficas

>> close all

Varias zonas gráficas en la misma ventana, subplot

El comando subplot(m,n,p) divide la ventana gráfica Figure Window en m×n ventanas rectangulares gráficas más pequeñas dispuestas en forma de matriz en m filas y n columnas. Cada ventana está numerada de 1 a m·n tal como se indica en la figura.

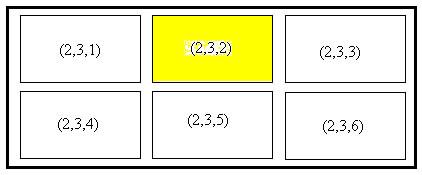
Por ejemplo el comando subplot(2,3,2) crea seis áreas rectangulares ordenadas en dos filas y tres columnas como se muestra en la figura y hace el área marcada en amarillo p=2 como actual.

La posición velocidad y energía de un oscilador amortiguado son, respectivamente.

${\displaystyle \begin{array}{l}x=A\exp (-\gamma t)\sin (\omega t+\phi ){\omega }^2={\omega }_0^2-{\gamma }^2\\ v=\frac{dx}{dt}=-\gamma A\exp (-\gamma t)\sin (\omega t+\phi )+A\omega \exp (-\gamma t)\cos (\omega t+\phi )\\ E=\frac{1}{2}m{v}^2+\frac{1}{2}m{\omega }_0^2{x}^2=\frac{1}{2}m{\omega }_0^2{A}^2\exp (-2\gamma t)\left(1-\frac{\gamma }{{\omega }_0}\sin \left(2({\omega }_{0}t+\phi )\right)\right)\end{array}}$

Sea un oscilador amortiguado de amplitud A=5.01, fase inicial φ=1.5 rad, frecuencia angular natural ω₀=100 rad/s y constante de amortiguamiento γ=7 s^-1

Creamos un script para

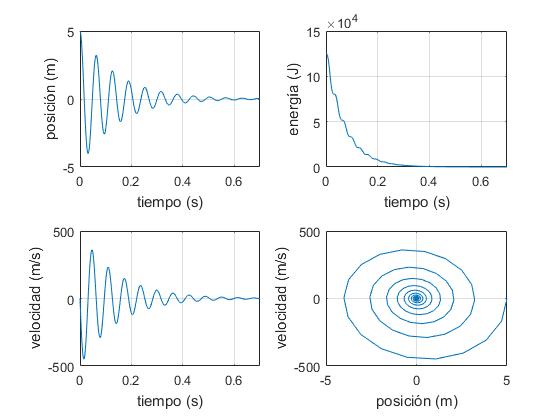
1. Dividir la ventana gráfica en cuatro zonas con el comando subplot
2. Representar en la primera zona, la posición x en función del tiempo t
3. Representar en la segunda, la energía e del oscilador en función del tiempo t
4. Representar en la tercera, la velocidad v del móvil en función del tiempo t
5. Respresentar en la cuarta, la velocidad del móvil v en función de su posición x (espacio de las fases)

g=7; %amortiguamiento
x0=5; %posición inicial 
v0=0; %velocidad inicial
w0=100;  %frecuencia natural
w=sqrt(w0^2-g^2); %frecuencia
x=@(t) exp(-g*t).*((v0+g*x0)*sin(w*t)/w+x0*cos(w*t));
v=@(t) -g*x(t)+exp(-g*t).*((v0+g*x0)*cos(w*t)-x0*w*sin(w*t));
e=@(t) (v(t).^2+w0*w0*x(t).^2)/2;

subplot(2,2,1)
fplot(x,[0,0.7])
grid on
xlabel('tiempo (s)')
ylabel('posición (m)')

subplot(2,2,2)
fplot(e,[0,0.7])
grid on
xlabel('tiempo (s)')
ylabel('energía (J)')

subplot(2,2,3)
fplot(v,[0,0.7])
grid on
xlabel('tiempo (s)')
ylabel('velocidad (m/s)')

subplot(2,2,4)
t=linspace(0,0.7,200);
plot(x(t),v(t))
grid on
xlabel('posición (m)')
ylabel('velocidad (m/s)')

Insertando una figura dentro de otra

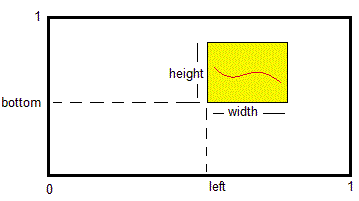
En ciertas situaciones puede interesar insertar una o más figuras secundarias dentro de otra figura principal. Se lleva a cabo mediante el comando

axes('Position',[left,bottom,width,height])

Position es un vector que define la posición y dimensiones de la región rectangular que se inserta en la figura principal, sus valores van de 0 a 1, tal como se muestra en la figura

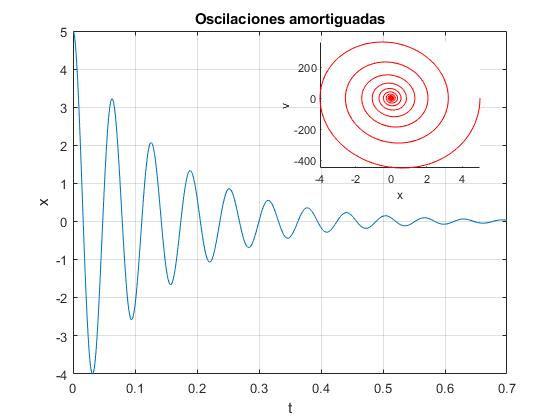
En este ejemplo, representamos una oscilación amortiguada. En la figura principal, la posición en función del tiempo, y en la figura insertada, la velocidad en función de la posición (espacio de las fases)

g=7; %amortiguamiento
x0=5; %posición inicial 
v0=0; %velocidad inicial
w0=100;  %frecuencia natural
w=sqrt(w0^2-g^2); %frecuencia
x=@(t) exp(-g*t).*((v0+g*x0)*sin(w*t)/w+x0*cos(w*t));
fplot(x,[0,0.7]);
grid on
xlabel('t')
ylabel('x')
title('Oscilaciones amortiguadas')

axes('Position',[4/7,6/10,2/7,3/10])
v=@(t) -g*x(t)+exp(-g*t).*((v0+g*x0)*cos(w*t)-x0*w*sin(w*t));
fplot(x,v,[0,0.7],'color','r');
xlabel('x')
ylabel('v')
box off

Ejemplos

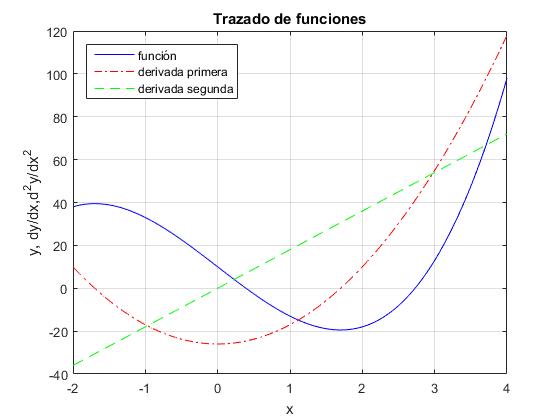
1.- Dibujar la función y=3x³-26x+10, su derivada primera y su derivada segunda, en el intervalo -2≤x≤4, en la misma gráfica con distintos colores.

x=linspace(-2,4,200);
y(1,:)=3*x.^3-26*x+10;
y(2,:)=9*x.^2-26;
y(3,:)=18*x;
plot(x,y)
legend('función','derivada primera','derivada segunda', 'Location','northwest')
xlabel('x')
ylabel('y, dy/dx,d^2y/dx^2')
title('Trazado de funciones')
grid on

Con distintos colores y estilo de línea.

x=linspace(-2,4,200);
y=3*x.^3-26*x+10;
y1=9*x.^2-26;
y2=18*x;
plot(x,y,'b',x,y1,'-.r',x,y2,'--g')
legend('función','derivada primera','derivada segunda','Location','northwest')
xlabel('x')
ylabel('y, dy/dx,d^2y/dx^2')
title('Trazado de funciones')
grid on

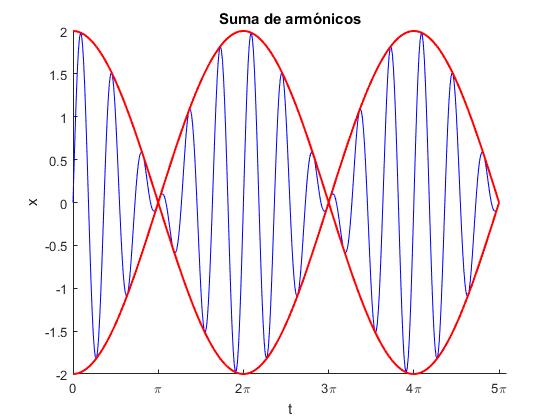
2.- Dibujar la superposición x₁+x₂ de dos Movimientos Armónicos Simples de la misma dirección y distinta frecuencia en el intervalo 0≤t≤4π,

x₁=sin(t)
x₂ =sin(2t)

${\displaystyle x_1+x_2=2\cos \left(\frac{1}{2}t\right)\sin \left(\frac{3}{2}t\right)}$

Superponer en el mismo gráfico la amplitud modulada (envolvente) en color diferente y con grosor de línea 1.5

t=linspace(0,5*pi,400);
x=sin(5*t)+sin(6*t);
y=2*cos(0.5*t);
hold on
plot(t,x,'b')
plot(t,y,'r','linewidth',1.5)
plot(t,-y,'r','linewidth',1.5)
hold off
title('Suma de armónicos')
xlabel('t')
ylabel('x')
set(gca,'XTick',0:pi:5*pi)
set(gca,'XTickLabel',{'0','\pi','2\pi','3\pi','4\pi','5\pi'})

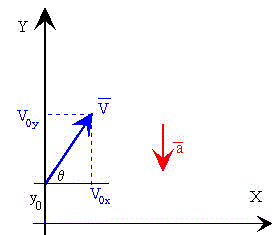
Un cuerpo se lanza desde la altura y₀ con velocidad v₀, que hace un ángulo θ con la horizontal. Las ecuaciones del movimiento son:

${\displaystyle \begin{array}{l}x=v_0\cos \theta ·t\\ y=y_0+v_0\sin \theta ·t+\frac{1}{2}(-g)t^2\end{array}}$

La ecuación de la trayectoria del móvil es

${\displaystyle y=y_0+x\tan \theta -\frac{g}{2}\frac{x^2}{v_0^2{\cos }^2\theta }=y_0+x\tan \theta -x^2\frac{g}{2v_0^2}\left(1+{\tan }^2\theta \right)}$

Dados los datos de la altura inicial y₀, la velocidad inicial v₀ y el ángulo de tiro θ calcular el alcance horizontal y el tiempo de vuelo del proyectil, cuando llega al suelo y=0.

Escribir un script que realice las siguientes tareas:

1. Establezca mediante comandos input, los valores de la altura y₀, velocidad inicial v₀ y ángulo de tiro θ
2. Determine el tiempo de vuelo calculando una de las raíces de la ecuación de segundo grado
3. Calcular el alcance, conocido el tiempo de vuelo
4. Represente la trayectoria y la decore con título, etiquetas en el eje X y en el eje Y. Utilice el comando axis para estabecer nuevos valores máximos y mínimos para el eje X y para el eje Y distintos de los que MATLAB establece por defecto
5. Utilice el comando text, para que apareza en algún lugar de la gráfica, los datos del tiempo de vuelo y del alcance

Ejemplo: Un cañón dispara una bala desde lo alto de un acantilado de 100 m de altura con una velocidad de 46 m/s haciendo un ángulo de 30° por encima de la horizontal. Tomar g=10 m/s²

%entrada: altura, velocidad inicial y ángulo de tiro
y0=input('altura: ');
v0=input('velocidad inicial: ');
ang=input('ángulo:');
g=10;

%calcula el tiempo de vuelo tf, resolviendo la ecuación de segundo grado
a=-g/2; b=v0*sind(ang); c=y0;
tf=(-b-sqrt(b*b-4*a*c))/(2*a);
%calcula el alcance
xf=v0*cosd(ang)*tf;

%representación gráfica de la trayectoria 
x=linspace(0,xf,50);
y=y0+x*tand(ang)-x.ˆ2*(g/(2*v0*v0))*(1+tand(ang)*tand(ang));
plot(x,y,'r')
xlabel('x')
ylabel('y')
title('tiro parabólico')
grid on
axis([0,xf+50,-10,max(y)+10])

%marca el alcance con una línea horizontal de color negro
line([0 xf], [0 0],'color','k')

%dato del alcance 
text(xf,0,num2str(xf))
%dato del tiempo de vuelo
text(xf,max(y),'tiempo')
text(xf,max(y)-10,num2str(tf))

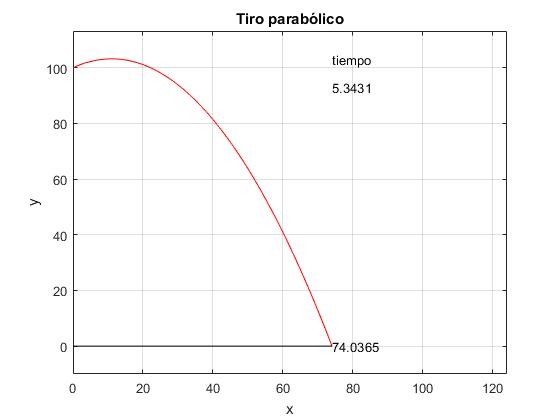
En la ventana de comandos corremos el script

altura: 100
velocidad inicial: 46
ángulo:30

La ecuación de la trayectoria de un cuerpo celeste en coordenadas polares es

${\displaystyle r=\frac{d}{1+\epsilon \cos \theta }}$

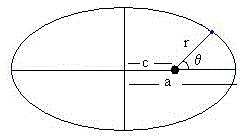
Un cuerpo celeste describe una trayectoria elíptica si la excentricidad ε<1.

Las relaciones que hay entre el semieje mayor a, la semidistancia focal c y los parámetros d y excentricidad ε de la elipse son:

${\displaystyle \begin{array}{l}2a=\frac{d}{1-\epsilon }+\frac{d}{1+\epsilon }d=a(1-{\epsilon }^2)\\ \epsilon =\frac{c}{a}\end{array}}$

Escribir un script que produzca una gráfica y que realice las siguientes tareas:

1. Establezca mediante el comando input, el valor de la excentricidad ε.
2. Fije el parámetro d=1
3. Dibuje la trayectoria elíptica

d=1;
e=input('excentricidad <1: ');
ang=0:pi/36:2*pi;
r=d./(1+e*cos(ang));
polar(ang,r,'r');
title('elipse')

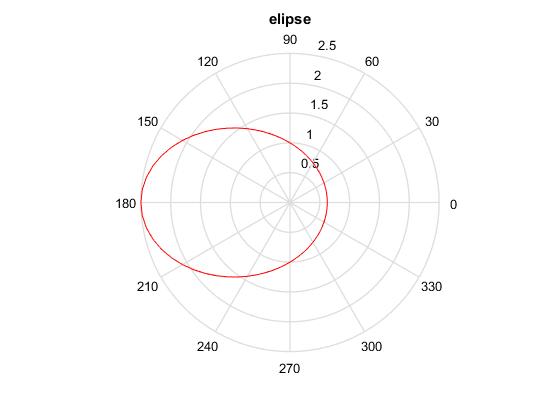
En la ventana de comandos corremos el script

excentricidad <1: 0.6

La ecuación de la trayectoria de un cuerpo en coordendas polares que se mueve bajo la acción de una fuerza atractiva es

${\displaystyle r=\frac{d}{\epsilon \cos (k\theta )+1}}$

Si la energía total E del cuerpo es negativa (E<0) entonces el parámetro ε<1, se presentan los casos más interesantes.

Cuando k se expresa como un número racional k=m/n el numerador m indica la simetría y el denominador n el número de vueltas que el radio vector da alrededor del origen. La órbita es cerrada siempre que k sea un número racional. Ejemplos: ε=0.5, k=6/1, k=7/6, k=1/3.

Crear un script en el que establezca mediante comandos input

• La excentricidad ε<1,
• El valor de k=m/n expresado como fracción (numerador m, denominador n).

Fijado el parámetro d=1, representar la trayectoria.

e=input('Excentricidad <1: ');
m=input('numerador: ');
n=input('denominador: ');
ang=0:pi/36:2*pi*n;
r=1./(1+e*cos(m*ang/n));
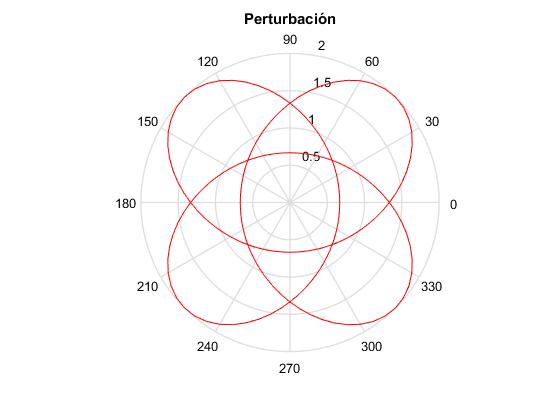
polar(ang,r,'r');
title('perturbación')

En la ventana de comandos corremos el script

Excentricidad <1: 0.5
numerador: 4
denominador: 3