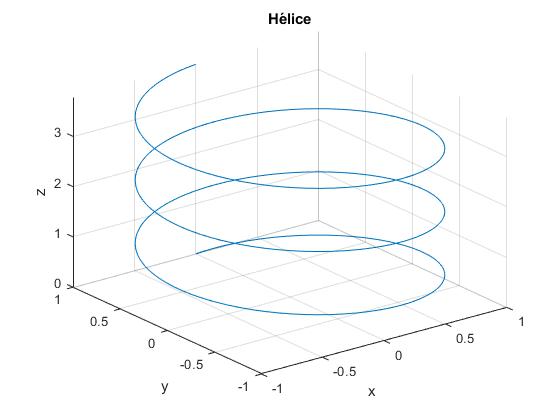
Gráficos tridimensionales

Curvas tridimensionales

El caso más sencillo se presenta cuando x, y y z son funciones de un parámetro t. Utilizamos el comando fplot3 para dibujar la línea tridimensional.

x=sin(t)
y=cos(t)
z=0.2·t

fplot3(@(t) sin(t), @(t) cos(t),@(t) 0.2*t, [0,6*pi])
grid on
xlabel('x'); 
ylabel('y'); 
zlabel('z')
title('Hélice')

Superficies tridimensionales

Algo más complicado es mostrar una superficie tridimensional descrita por una función de dos variables z=f(x,y)

El primer paso es crear una rejilla en el plano XY que cubra el dominio de la función y el segundo paso consiste en el cálculo del valor de z para cada uno de los puntos de la rejilla.

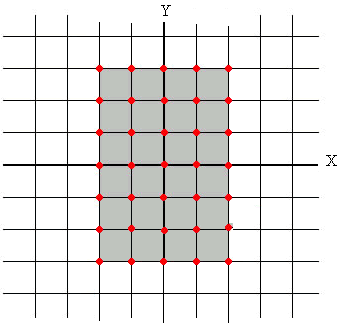
En la figura se muestra el conjunto de puntos del plano XY para el dominio -2≤x≤3, -1≤y≤3 con espaciado de una unidad. Los puntos de la rejilla se definen mediante dos matrices. La matriz X guarda las abscisas de los puntos y la matriz Y las ordendas de dichos puntos. La función meshgrid de MATLAB crea la matriz X y la matriz Y.

>> x=-2:2;
>> y=-3:3;
>> [X,Y]=meshgrid(x,y)
X =
    -2    -1     0     1     2
    -2    -1     0     1     2
    -2    -1     0     1     2
    -2    -1     0     1     2
    -2    -1     0     1     2
    -2    -1     0     1     2
    -2    -1     0     1     2
Y =
    -3    -3    -3    -3    -3
    -2    -2    -2    -2    -2
    -1    -1    -1    -1    -1
     0     0     0     0     0
     1     1     1     1     1
     2     2     2     2     2
     3     3     3     3     3

Se calculan los valores de z=f(x,y) para cada unos de los puntos de la rejilla. En este caso z=x²-y²

>> Z=X.^2-Y.^2
Z =
    -5    -8    -9    -8    -5
     0    -3    -4    -3     0
     3     0    -1     0     3
     4     1     0     1     4
     3     0    -1     0     3
     0    -3    -4    -3     0
    -5    -8    -9    -8    -5

Incrementamos la resolución y dibujamos la superficie mediante la función mesh,

x=-2:0.1:2;
y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z=X.^2-Y.^2;
mesh(X,Y,Z);
xlabel('X')
ylabel('Y')
zlabel('Z')

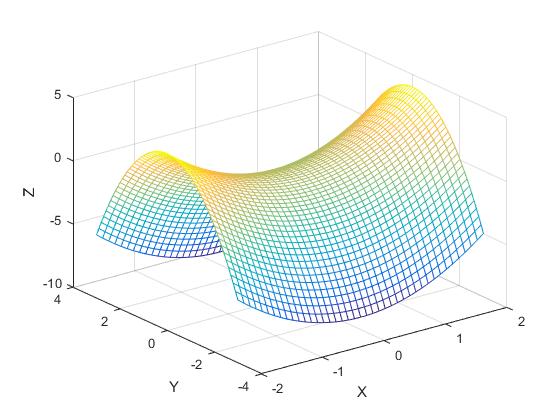
Alternativamente, podemos dibujar la misma superficie utilizando la función surf.

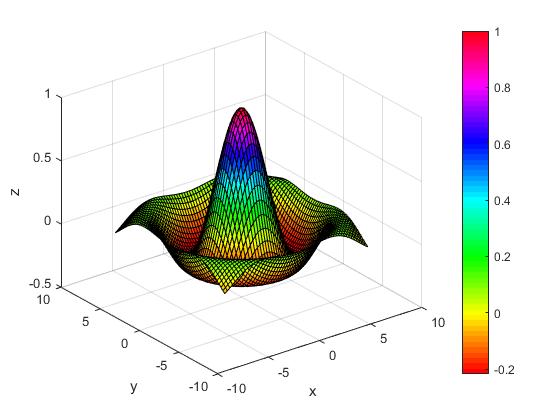
Vamos a dibujar la función

$z = \frac{\sin r}{r} r = \sqrt{x^{2} + y^{2}}$

en el dominio el dominio -7≤x≤7, -7≤y≤7 con espaciado de 0.25. Evitamos a indeterminación 0/0 en el origen sumando eps a r.

El color de cada elemento de superficie está determinado por el valor de z y el mapa de colores (una lista ordenda de colores)

[x,y] = meshgrid(-7:0.25:7);
r = sqrt(x.^2 + y.^2) + eps;
z = sin(r)./r;
surf(x,y,z)
colormap hsv
colorbar
xlabel('x'); ylabel('y'); zlabel('z')

Superficies definidas de forma paramétrica

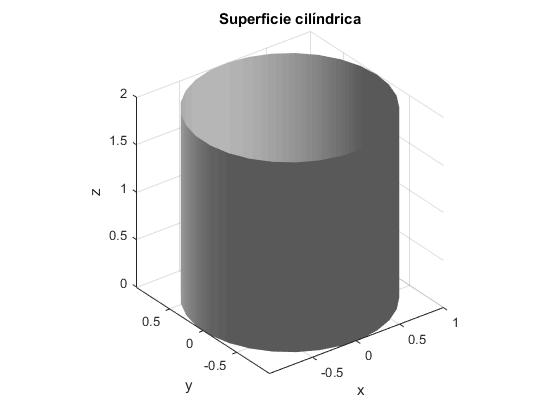
Cilindro

r=1*ones(30,1);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=repmat(linspace(0,2,30),30,1);
surfl(x,y,z);
shading interp
colormap(gray);

axis equal
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie cilíndrica')

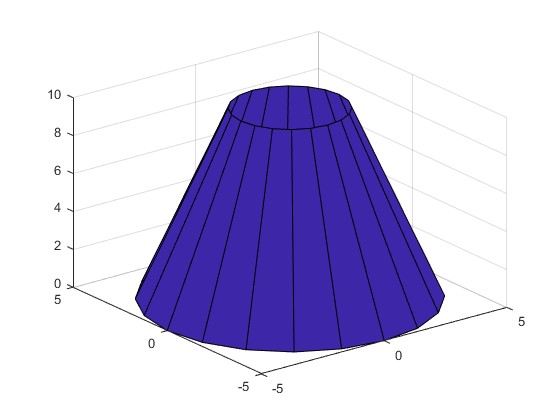
Con la función cylinder se representan cilindros y troncos de cono

[X,Y,Z]=cylinder([5,2]); %radios
Z=Z*10; %altura
surf(X,Y,Z)

Cono

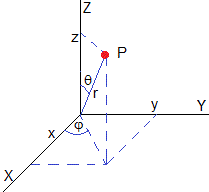
Coordenadas esféricas

x=r·cosφ·sinθ
y=r·sinφ·sinθ
z=r·cosθ

donde 0≤r≤1, 0≤φ≤2π, 0≤θ≤π/2

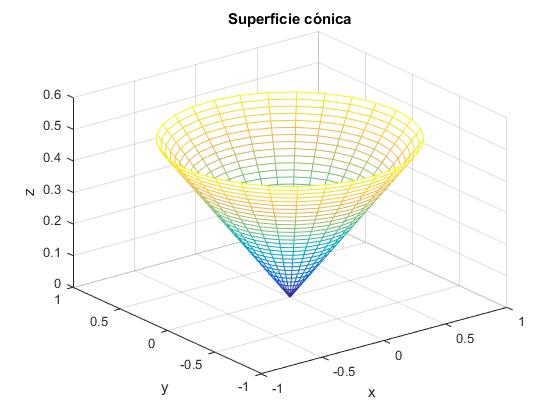
La superficie cónica se define para un valor θ fijo

theta=pi/3;
r=linspace(0,1,30);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
mesh(x,y,z)
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie cónica')

Esfera

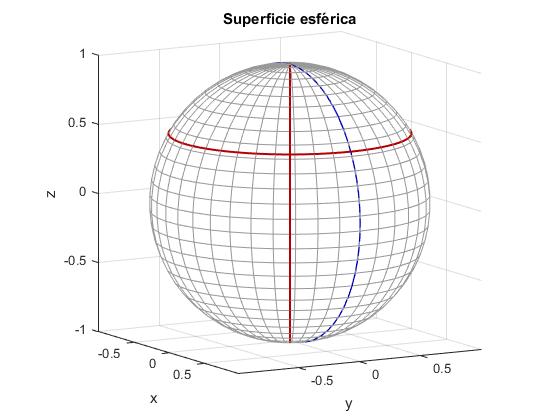
Dibujamos una superficie esférica, y sobre ella el punto P de coordenadas φ y θ

%esfera
R=1;
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(phi).*cos(theta);
y=R*sin(phi).*sin(theta);
z=R*cos(phi);
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6]);
%probar una superficie esférica semitransparente
%set(h1,'EdgeColor',[0.6,0.6,0.6],'EdgeAlpha',0.5,'FaceAlpha',0.5) 

%paralelo
theta=pi/3;
phi=0:0.1:2*pi+0.1;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta)*ones(1,length(x));
h1=line(x,y,z);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
%meridiano de referencia
phi=0;
theta=-pi:0.1:pi;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta);
h1=line(x,y,z);
set(h1,'Color',[0,0,.7],'LineWidth',1)
%meridiano
phi=-pi/6;
theta=-pi:0.1:pi;
x=sin(theta)*cos(phi);
y=sin(theta)*sin(phi);
z=cos(theta);
h1=line(x,y,z);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)

axis equal
view(60,10)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie esférica')

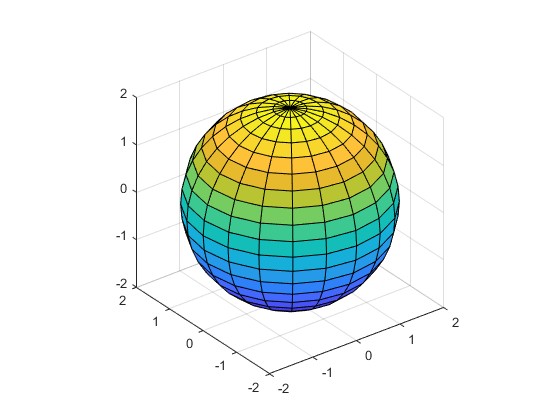
Representamos una esfera de radio r=2 mediante la función sphere

[X,Y,Z] = sphere;
r=2; %radio de la esfera
X=X*r;
Y=Y*r;
Z=Z*r;
surf(X,Y,Z)
axis equal

Superficies de revolución

Al girar alrededor del eje Z la función z=f(x), obtenemos una superficie de revolución

La energía potencial de una masa puntual situada en el origen es E_p(r)=-k/r. Su representación en el plano es

z=@(x) -1./abs(x);
hold on
fplot(z,[1,5],'b')
fplot(z,[-5,-1],'b')
line([0,0],[-0.2,-1], 'lineStyle','--','color','k','lineWidth',1.5)
hold off
grid on
xlabel('x')
ylabel('z')
title('Superficies de revolución')

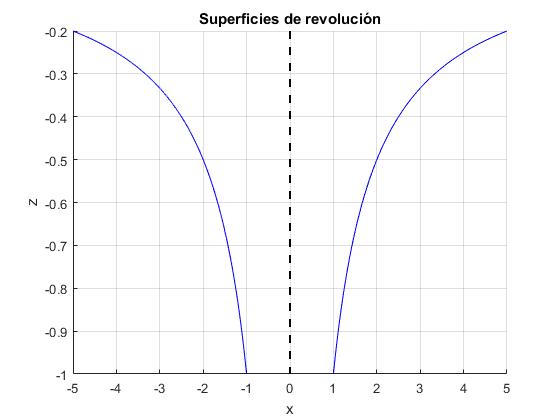
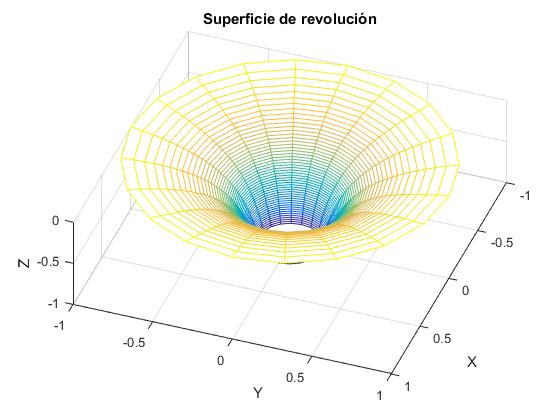
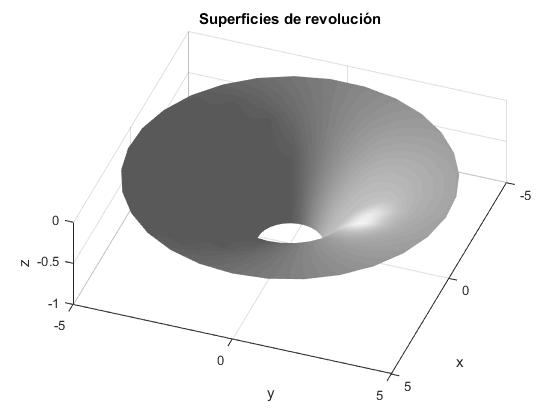
Al girar las gráficas (en color azul) alrededor del eje vertical Z, marcado por la línea a trazos, obtenemos una superficie de revolución. Utilizamos la función cylinder de MATLAB

x=linspace(1, 5, 50);
z=1./x; 
[X,Y,Z]=cylinder(z);
mesh(X,Y,-Z);
xlabel('X'); ylabel('Y'); zlabel('Z') 
title('Superficies de revolución')
view(110,68)

Otra forma de vusualizar la superficie de revolución sin utilizar la función cylinder

r=linspace(1,5,50);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=1./r;

surfl(x,y,-z)
shading interp
colormap(gray);
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficies de revolución')
view(110,68)

Simetría

En la página titulada Gráficos bidimensionales (I), hemos estudiado cómo se representan las funciones simétricas y antisimétricas, utilizando la función fliplr de MATLAB

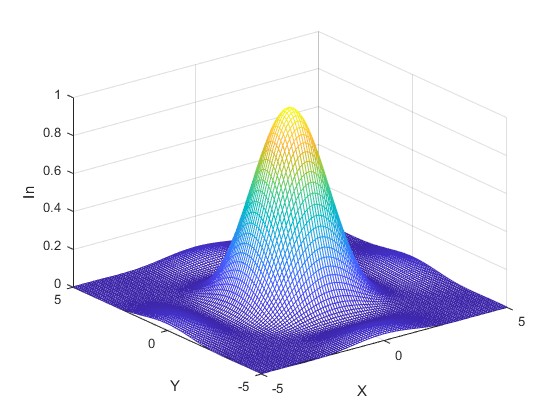
En este apartado, representamos una función que es simétrica respecto del eje X y del eje Y, por lo que solamente es necesario calcular la función en el primer cuadrante. Seguimos los pasos del ejemplo 6, de la página titulada Matrices

La función que valos a representar es

$f (x, y) = {(\frac{\sin x}{x})}^{2} {(\frac{\sin y}{y})}^{2}$

[X,Y]=meshgrid(eps:0.1:5);
M=((sin(X)./X).^2).*((sin(Y)./Y).^2);
M=flipud(M); %primer cuadrante
[m,n]=size(M);
E=zeros(m,2*n-1);
E(1:m,n:2*n-1)=M;
E(1:m,1:n-1)=fliplr(M(1:m,2:n));
F=flipud(E(1:m-1,:));
H=[E;F];
[X,Y]=meshgrid(-5:0.1:5);
mesh(X,Y,H);
xlabel('X')
ylabel('Y')
zlabel('In')

Ejemplos

1.-Tiro parabólico 3D

Se dispara un proyectil con velocidad de 60 m/s haciendo un ángulo de 30°, desde la ventana del vagón de un tren en movimiento a lo largo del eje X con velocidad de 20 m/s. Tómese g=10 m/s²

Calcular la altura máxima y las coordendas (x,y) del punto de impacto.
Representar la trayectoria del proyectil

Ecuaciones del movimiento

${\begin{cases} a_{x} = 0 \\ a_{y} = 0 \\ a_{z} = - 10 \end{cases} {\begin{cases} v_{x} = 20 \\ v_{y} = 30 \sqrt{3} \\ v_{z} = 30 - 10 \cdot t \end{cases} {\begin{cases} x = 20 t \\ y = 30 \sqrt{3} \cdot t \\ z = 30 \cdot t - 5 \cdot t^{2} \end{cases}$

El proyectil alcanza la máxima altura cuando v_z=0, en el instante t=3 s, la altura es de z_max=45 m.

El proyectil impacta contra el suelo cuando z=0, en el instante t=6 s. En este instante las coordenadas del punto de impacto son: x=120 m, y=311.8 m

t=linspace(0,6,50);
z=30*t-5*t.^2;
y=30*sqrt(3)*t;
x=20*t;
plot3(x,y,z)
grid on
axis([0 150 0 350 0 50])
xlabel('x (m)'); ylabel('y (m)'); zlabel('z (m)')
view(50,20)

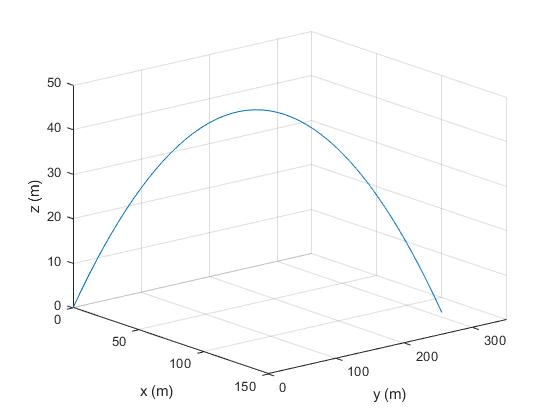
Utilizar la herramienta Rotate 3D del menú Figure Window para cambiar el ángulo de visualización de la parábola.

2.-Dibujar al función

$\begin{array}{l} z = \frac{x y^{2}}{x^{2} + y^{2}} \\ - 1 \leq x \leq 3 1 \leq y \leq 4 \end{array}$

x=-1:0.1:3;
y=1:0.1:4;
[X,Y]=meshgrid(x,y);
Z=(X.*Y.^2)./(X.^2+Y.^2);
mesh(X,Y,Z);
xlabel('X')
ylabel('Y')
zlabel('Z')
view(50,20)

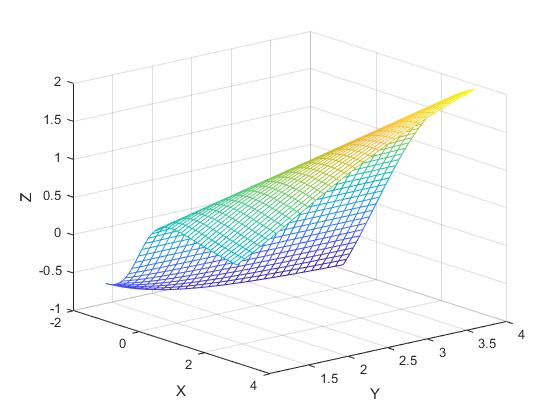
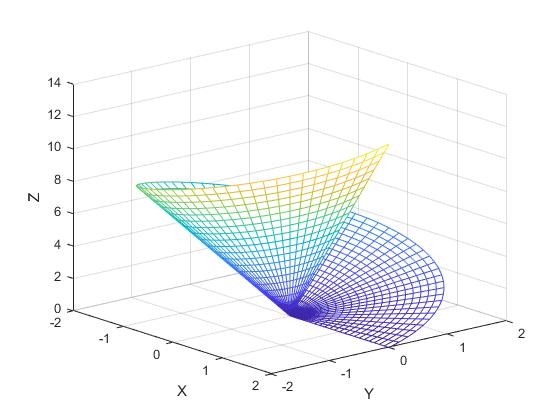
3.- Dibujar la función

$\begin{array}{l} z = r θ \\ 0 \leq θ \leq 360 0 \leq r \leq 2 \end{array}$

Utilizar la función pol2cart para convertir coordenadas polares a coordenadas rectangulares.

r=0:0.1:2;
angulo=(0:5:360)*pi/180;
[Ang,Radio]=meshgrid(angulo,r);
Z=Radio.*Ang;
[X,Y] = pol2cart(Ang,Radio);
mesh(X,Y,Z)
xlabel('X')
ylabel('Y')
zlabel('Z')
view(50,20)

4.-Un menisco

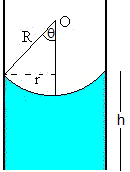
Cuando un líquido asciende por un tubo capilar, la columna de líquido tiene forma de cilindro pero su base superior no es plana, es semejante a una parábola de revolución, pero la podemos aproximar por un casquete esférico

Representamos en tres dimensiones el cilindro y el casquete esférico para R=1 y θ=π/6. La altura del cilindro es h=0.5

ang=pi/6;
%cilindro
R=1;
r=R*sin(ang)*ones(30,1);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=repmat(linspace(0,0.5,30),30,1);
hold on
surfl(x,y,z);

%casquete esférico
phi=linspace(0,ang,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=R*sin(phi).*cos(theta);
y=R*sin(phi).*sin(theta);
z=0.5+R*cos(ang)-R*cos(phi);
surfl(x,y,z);
shading interp
colormap(gray);
hold off
axis equal
axis off
view(9,18)

Campos de pendientes, soluciones

Una ecuación diferencial de primer orden es

$\frac{d y}{d x} = f (x, y)$

meshgrid crea una rejilla de puntos en el plano XY y quiver dibuja un vector en cada punto cuya pendiente es f(x,y)

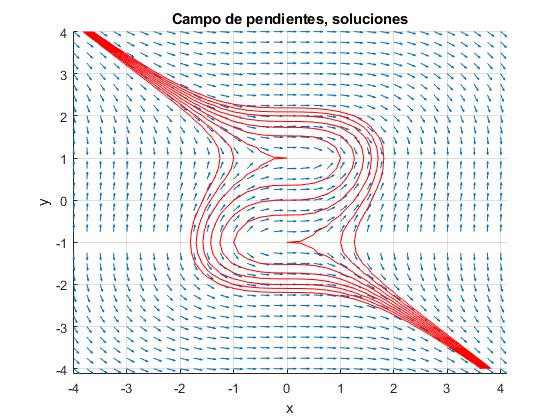
F(x,y)=c, es la solución de la ecuación diferencial, donde c es la constante de integración. Representamos algunas de las soluciones mediante contour para varios valores de dicha constante c

Ejemplo 1:

Sea la ecuación diferencial

$\frac{d y}{d x} = \frac{x^{2}}{1 - y^{2}}$

La solución es

$\begin{array}{l} \int x^{2} d x = \int (1 - y^{2}) d y + c \\ \frac{x^{3}}{3} - y + \frac{y^{3}}{3} = c \\ x^{3} - 3 y + y^{3} = c \end{array}$

[X Y]=meshgrid(-4:0.25:4,-4:0.25:4);
dY=X.^2./(1-Y.^2);
dX=ones(size(dY));
L=sqrt(1+dY.^2); %escala, longitud vector ds=sqrt(dx^2+dy^2)
hold on
quiver(X, Y, dX./L, dY./L, 0.5) %misma longitud vectores
contour(X,Y,X.^3-3*Y+Y.^3,-4:1:4, 'color','r');
hold off
axis tight
grid on
xlabel ('x')
ylabel ('y')
title ('Campo de pendientes, soluciones')

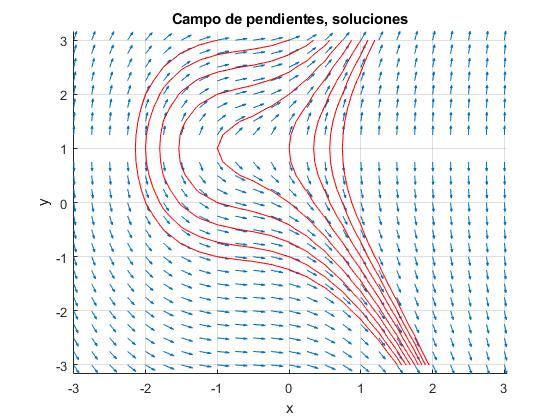
Ejemplo 2:

$\frac{d y}{d x} = \frac{3 x^{2} + 4 x + 2}{2 (y - 1)}$

La solución es

$\begin{array}{l} \int (3 x^{2} + 4 x + 2) d x = \int (2 (y - 1)) d y + c \\ x^{3} + 2 x^{2} + 2 x - y^{2} - 2 y = c \end{array}$

[X Y]=meshgrid(-3:0.25:3,-3:0.25:3);
dY=(3*X.^2+4*X+2)./(2*(Y-1));
dX=ones(size(dY));
L=sqrt(1+dY.^2); %escala, longitud vector ds=sqrt(dx^2+dy^2)
hold on
quiver(X, Y, dX./L, dY./L, 0.5) %misma longitud vectores
contour(X,Y,Y.^2-2*Y-X.^3-2*X.^2-2*X,-4:1:4, 'color','r');
hold off
axis tight
grid on
xlabel ('x')
ylabel ('y')
title ('Campo de pendientes, soluciones')

Referencias

James R. Brannan, William E. Boyce. Differencial equations. An Introduction to Modern Methods and Applications.. John Wiley & Sons, Inc. 2002, pp.45-48

Curvas de nivel

Representamos gráficamente la función

$f (x, y) = \sin (x) \exp (- \frac{y}{2})$

x=0:0.1:pi;
y=0:0.1:3;
[X,Y]=meshgrid(x,y);
Z=sin(X).*exp(-Y/2);
mesh(X,Y,Z);
xlabel('X')
ylabel('Y')
zlabel('f(x,y)')

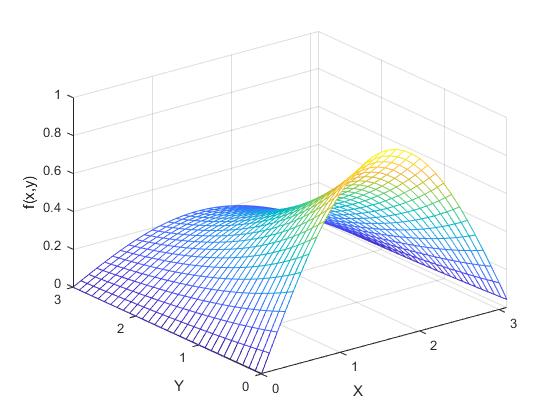
Utilizamos fcontour para mostrar las curvas de nivel f(x,y)=c

f=@(x,y) sin(x).*exp(-y/2);
fcontour(f,[0,pi,0,3])
xlabel('x')
ylabel('y')
title('f(x,y)')

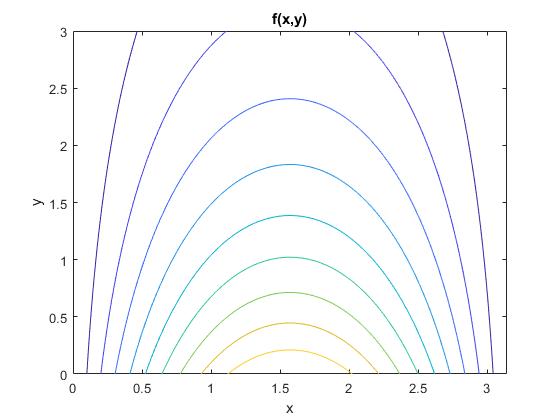
Si estamos interesados en ciertos valores de la constante c lo especificamos con LevelList

f=@(x,y) sin(x).*exp(-y/2);
fcontour(f,[0,pi,0,3],'LevelList',0.2:0.2:1)
grid on
xlabel('x')
ylabel('y')
title('f(x,y)')

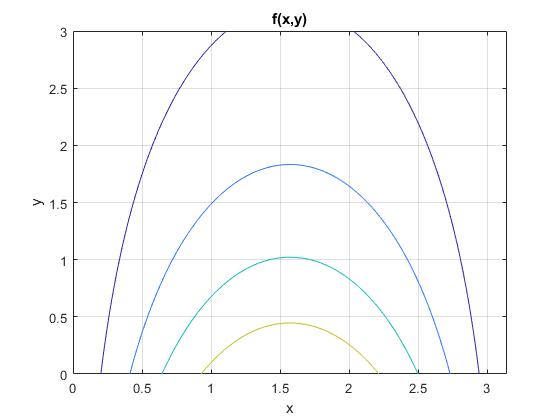
Otra forma de ver las curvas de nivel de la función

f=@(x,y) sin(x).*exp(-y/2);
fcontour(f,[0,pi,0,3], 'fill','on')
colorbar
xlabel('x')
ylabel('y')
title('f(x,y)')

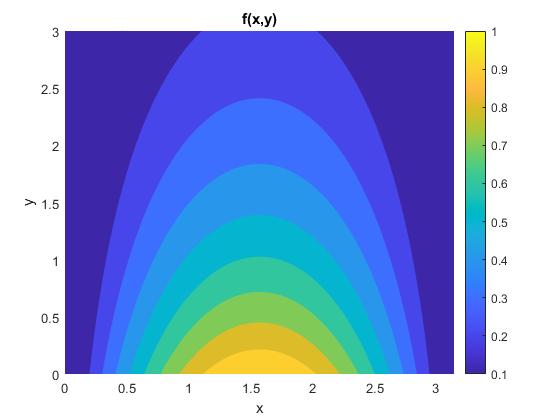
Ejemplos en el curso de Física

Movimiento relativo de rotación uniforme

Modos de vibración de una membrana rectangular

Modos de vibración de una membrana circular

Posición del Sol en el Sistema de Referencia Local